La R.O. è un metodo scientifico atto a fornire ai dirigenti aziendali una base quantitativa per le decisioni concernenti le operazioni sottoposte al controllo.

Per quanto ci riguarda intenderemo la R.O. come l'insieme dei metodi e dei modelli matematici rivolti alla risoluzione di alcuni particolari problemi di scelta.

BREVE CENNO STORICO

All'origine la R.O. è scorta in relazione all'esigenza di risolvere problemi bellici diversi. Vista in quest'ottica la R.O. ha indubbiamente origini origini molto remote. Sta di fatto, per,ò che soltanto poco prima che scoppiasse il primo conflitto mondiale la R.O. assume una propria precisa fisionomia come speciale br 232h77c anca delle attività di ricerca. Essa, subisce particolare impulso, specialmente in Inghilterra e negli Stati Uniti, intorno al 1939. Infatti, è proprio nel 1939 che alcuni militari della R.A.F., cioè dell'aeronautica militare inglese, costituiscono un gruppo di ricerca per studiare sistemi ottimali di offesa e di difesa. Il gruppo, composto da chimici, fisici, matematica e naturalmente, strateghi della R.A.F., si chiamò circolo Blackett dal nome dello scienziato che lo dirigeva e che oggi è considerato come uno dei padri della R.O.. Finita la guerra, gli studi di R.O., pur continuando a essere coltivati in campo militare, dove erano nati, si rivolsero a problemi economici e sociali ed oggi gli interessi non militari della R.O. sono certamente quelli che prevalgono.

CARATTERI E STRUMENTI DELLA R.O.

I caratteri distintivi di un lavoro di R.O. sono:

a)  l'esistenza di un problema di scelta;

b)  la possibilità di esprimere numericamente i risultati delle varie alternative;

c)  la costruzione di un modello logico (generalmente matematico) che rappresenti la realtà e sul quale sia possibile sperimentare l'effetto di decisioni alternative.

Non sempre i problemi sono chiaramente impostati e nettamente individuati nei loro contorni. Spetta al ricercatore operativo individuarli esplicitando gli obbiettivi del decisore ed esprimendo numericamente i vari risultati.

Gli strumenti di lavoro di un ricercatore operativo sono: l'analisi di un problema e la creazione di un modello richiedono conoscenze di vario tipo: nozioni di statistica, di matematica, d'informatica,... Spesso i tradizionali metodi d'analisi per la ricerca degli estremi non sono sufficienti per individuare la migliore soluzione di un problema di R.O. : le variabili ed i vincoli possono essere in numero elevato; le espressioni analitiche della funzione obbiettivo ed i vincoli possono risultare troppo complesse per una trattazione tradizionale. Per questo che sono stati creati e messi a punto dei procedimenti speciali che vanno, appunto, sotto il nome di R.O.. Solo l'esame comparato di vie alternative che conduce a scelte sicure, o almeno razionali, entro i limiti concessi dalla prevedibilità del sistema.

PROBLEMI TIPICI DELLA R.O.

Se ci limitiamo a considerare i problemi aziendali dobbiamo riconoscere che tradizionalmente la R.O. ha trovato le sue maggiori applicazioni nel settore della produzione. Il citato metodo del Simplesso è stato ideato da Dantzig nel 1948 mentre studiava un problema di miscelazione di benzine per una grande compagnia petrolifera americana.

Da tener presente anche che, naturalmente, la filosofia della R.O. e gli strumenti più collaudati di essa non si applicano soltanto ai tipici problemi delle imprese private, o pubbliche, ma a tutti i problemi di gestione delle risorse, da quelle energetiche e tecnologiche a quelle economiche, infrastrutturali, sociali ed urbane.

COME PROCEDERE NELLA R.O.

L'analisi matematica rappresenta, una parte relativamente contenuta del lavoro globale richiesto a uno studioso di R.O.

Le fasi di uno studio di R.O. possono essere così schematizzate:

individuazione del problema;

raccolta dei dati;

costruzione di un modello rappresentativo del problema;

determinazione della soluzione;

messa a punto e collaudo del modello e della soluzione;

interpretazione dei risultati e relazione per i decisori.

INDIVIDUAZIONE DEL PROBLEMA

I problemi vanno anzitutto scoperti. Conoscere un problema significa conoscere le varie alternative possibili. Per poter scegliere razionalmente occorre anzitutto ben chiari gli obbiettivi.

Nella fissazione di questi, benché sia spesso necessario ridurre gli obbiettivi generali d'impresa a sub-obbiettivi parziali, è bene avere la vista lunga: uno studio di R.O. dovrebbe mirare a soluzioni che siano ottimali per tutta l'organizzazione piuttosto che per un solo settore. Normalmente come obbiettivo generale d'impresa si assume il massimo profitto a lunga scadenza oppure, se si tratta d'aziende d'erogazione, la fornitura di un dato servizio al minimo costo.

RACCOLTA DATI

Accade che il Ricercatore Operativo debba calcolarli direttamente non fosse altro che per averli in una determinazione utile per gli scopi che deve raggiungere.

COSTRUZIONE DEL MODELLO

Il modello matematico non è altro che una rappresentazione ideale della realtà, rappresentazione realizzata facendo ricorso ad appositi simboli ed espressioni matematiche

DETERMINAZIONE DELLA SOLUZIONE

La R.O. afferma di cercare la soluzione ottima di un certo problema in realtà si mira a trovare soltanto la soluzione migliore compatibile con le informazioni di cui si dispone. A tal proposito occorre osservare che:

a)  la soluzione alla quale si perviene, anche se ottimale, lo è per il modello considerato. Ciò, però, non assicura che lo sia per il problema. In ogni caso, se il modello è ben costruito la soluzione trovata costituirà senz'altro una buona approssimazione della soluzione del problema.

b)  Molto spesso l'individuazione della soluzione ottimale in senso assoluto tra le numerose possibili è così laboriosa da non essere assolutamente conveniente.

I problemi pratici vengono risolti con metodi cosiddetti euristici (frutto d'invenzione intellettuale), che non conducono con certezza ad una soluzione ottimale ma assicurano il raggiungimento di una buona soluzione,prossima all'ottimale, con una spesa ragionevole.   

MESSA A PUNTO E COLLAUDO DEL MODELLO E DELLA SOLUZIONE

Il criterio per giudicare la validità consiste nel verificare se c'è profonda corrispondenza tra le previsioni del modello e quello che accadrebbe nella realtà. Quando si parla di messa a punto e collaudo del modello e della sua soluzione vuol dire, controllare il modello per vedere se il suo output è plausibile. Da questa verifica si ottengono due risultati: veramente ottimale e falsamente ottimale.

INTERPOLAZIONE DEI RISULTATI  E RELAZIONE PER I DECISORI

Può accadere che in presenza di un problema concreto ci si trovi, per motivi diversi, nell'impossibilità di giungere alla costruzione di un' idoneo modello. Tale fatto non è di per sé una sconfitta definitiva: il fatto d'aver analizzato il problema e di averlo individuato in certi suoi tratti essenziali può portare già avanti sulla strada di una maggiore realizzazione della gestione di quel particolare problema.

PROGRAMMAZIONE LINEARE

STORIA DELLA PROGRAMMAZIONE LINEARE

La nascita della Programmazione Lineare risale al 1951, anno in cui uno studioso della Rand Corporation, G.B. Dantzig, ne fece la presentazione. In quell'occasione G.B. Dantzig presentò il metodo della Programmazione Lineare nella sua primitiva formulazione.

PROGRAMMAZIONE LINEARE A DUE E Più VARIABILI

In sostanza un problema di Programmazione Lineare non è altro che un problema di ricerca di massimo ( minimo ) di una funzione lineare sottoposta a vincoli lineari. La funzione può presentare due o più variabili per cui si possono avere problemi di Programmazione Lineare a due variabili e problemi di Programmazione Lineare a più di due variabili.

PROGRAMMAZIONE LINEARE A DUE VARIABILI

DEFINIZIONE DEL PROBLEMA

Si ha un problema di programmazione lineare quando, data una funzione lineare di due variabili, si vuole ricercare il massimo ( minimo) subordinatamente all'esistenza di vincoli lineari (disequazioni di primo grado in due incognite).

Precisamente, se:

z = p₁x+p₂y

è funzione lineare, di essa si ricerca il massimo (minimo) subordinatamente:

a)  ai vincoli:

x y

che prendono il nome di vincoli di segno;

b)  ad altri vincoli lineari espressi sotto forma di disuguaglianze deboli: vincoli tecnici.

PRECISAZIONI IN MERITO AI VINCOLI

Per quanto riguarda i vincoli, che hanno forza di disuguaglianze deboli, occorre fere qualche precisazione.

a)  i vincoli limitano la ricerca dei valori di x e di y che rendono massima ( minima ) la funzione z in una determinata regione del piano.

Osservazione: con riferimento alla trattazione di problemi economici si dice che i vincoli sotto forma di disuguaglianza deboli definiscono il campo di scelta, cioè la regione del piano in cui vanno ricercati i valori di x e di y che rendono massima ( minima ) la funzione.

Esempio:

x y

4x + y

x + 3y

b)  Facendo riferimento ad un sistema di assi cartesiani xOy il campo di scelta viene rappresentato graficamente dalla regione del piano in cui soddisfano con le loro coordinate tutti i vincoli esistenti. E, poiché esistono sempre i vincoli di segno x e y , ne segue che la rappresentazione del campo di scelta va effettuata utilizzando soltanto il primo quadrante. 

RISOLUZIONE DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE

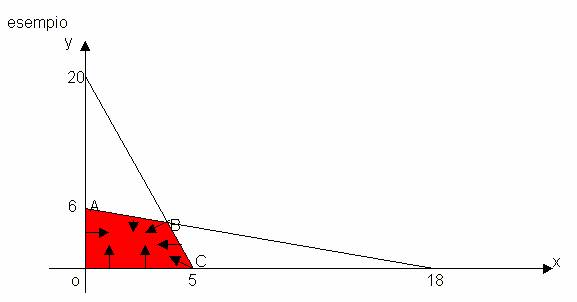
REGOLA: Per risolvere un problema di programmazione lineare occorre determinare i vertici del poligono che rappresenta il campo di scelta calcolando il valore che la funzione assume in ciascuno d'essi. Confrontando i valori così ottenuti si determina il massimo (minimo) della funzione.

La regola ora enunciata è una conseguenza del seguente fondamentale:

Teorema: In un problema di programmazione lineare il massimo (minimo) può cadere soltanto in un vertice del campo di scelta.

IMPORTANZA DELLA RAPPRESENTAZIONE GRAFICA NELLA RISOLUZIONE DI UN PROBLEMA DI P.L.

Se per un qualsiasi motivo, si tralasciasse di fare la rappresentazione grafica nel campo di scelta la mole di calcoli da eseguire per individuare quei vertici sarebbe notevolmente superiore.

La non rappresentazione preliminare del campo di scelta comporterebbe la risoluzione di 10 sistemi mentre la preliminare rappresentazione del campo di scelta fa scendere a 5 il numero dei sistemi da risolvere.

Ecco dunque emergere la fondamentale importanza della rappresentazione grafica del campo di scelta. Essa riduce, notevolmente il numero di sistemi che occorre risolvere per determinare i vertici fra i quali andrà poi ricercato il massimo ( minimo ).

CARATTERIZZAZIONE DEI VERTICI DEL CAMPO DI SCELTA

Il vertice del campo di scelta è qualsiasi punto in cui due vincoli sono realizzati sotto forma d'uguaglianza e i restanti sotto forma di disuguaglianza. Perché un vertice , inteso come punto d'intersezione  di due vincoli, sia accettabile come vertice del campo di scelta occorre che esso soddisfi, con le sue coordinate, tutti gli altri vincoli sotto forma di disuguaglianze.

PROGRAMMAZIONE LINEARE A TRE E PIU' VARIABILI

In generale, se le variabili sono m e i vincoli sono n il modello matematico, cioè l'insieme della funzione da ottimizzare, e dei vincoli si presenta come segue:

z = p₁x₁+p₂x₂+p₃x₃+.+p_mx_m

a₁₁x₁+a₁₂x₂+.+a_1mx_m b₁

a₂₁x₁+a₂₂x₂+.+a_2mx_m b₂

a_n1x₁+a_n2x₂+.+a_nmx_m b_n

con:

x₁ 0 x₂ 0 .... x_n 0

essendo

p_1,p₂,.,p_n : i coefficienti delle incognite ;

b_1,b₂,.,b_n : le risorse disponibili;

a₁₁,a₁₂,.,a₂₁,a₂₂,., a_n1,a_n2,.,a_{nm :}  i coefficienti di assorbimento delle risorse disponibili.

Premesso che in linea teorica si potrebbe procedere come fatto nel caso di due sole variabili, precisiamo subito che, sotto il profilo operativo concreto, s'incontrerebbero ben presto difficoltà praticamente insormontabili.

ALGORITMO DEL SIMPLESSO

Il simplesso è un metodo iterativo che permette di fare un'opportuna selezione dei vertici. Precisamente esso fornisce un criterio sistematico per potere, senza determinare preventivamente tutti i vertici, passare da un vertice accettabile ad un altro vertice che, essendo pure accettabile , è anche migliore del precedente.

Sostanzialmente, il simplesso si basa sulla seguente considerazione:

Poiché il P.L. la funzione obiettivo e i vincoli sono lineari e la ragione ammissibile come campo di scelta è convessa , se un vertice è miglior, in termini di funzione obbiettivo, dei vertici ad esso adiacenti esso è allora sicuramente l'ottimo fra tutti i vertici accettabili.

INTRODUZIONE DI VARIABILI SLACK

Il problema che si vuole risolvere viene dapprima modificato, sebbene soltanto formalmente, trasformando tutte le disequazioni (ad eccezione di quelle riguardanti i vincoli di segno) in equazioni. Questa trasformazione è possibile introducendo, inizialmente per ogni vincolo, una variabile fittizia, detta slack la quale deve sottostare soltanto al vincolo di segno, che resta sempre sottointeso. Da tener presente che le variabili slack non figurano nella funzione obbiettivo. Il motivo per cui vengono introdotte le variabili slack è in sostanza, questo: dopo l'introduzione delle variabili slack ogni vertice viene individuato da tanti zeri quante sono le variabili libere del problema.

L'APPLICAZIONE DEL SIMPLESSO DOPO L'INTRODUZIONE DELLE VARIABILI SLACK.

Prima si determina per ogni variabile che si vuole attivare quale variabile si deve annullare ( per non uscire dal campo di scelta ), poi si determina quale variabile conviene attivare perché y aumenti ed aumenti il più possibile. Il procedimento si ripete fino a quando si trova che l'attivazione di una qualunque variabile nulla farebbe diminuire e non aumentare y. Si è allora trovato il vertice massimo.

DUALITA'

Una delle più importanti scoperte che si ebbero come risultato degli studi sui problemi di P.L. fu il concetto di dualità. Questa scoperta rivelò che ogni problema di programmazione lineare associato con un altro problema pure di programmazione lineare, che viene detto "duale" e le cui relazioni con il problema originario detto primale, non sono soltanto di natura formale.

Consideriamo il seguente problema di programmazione lineare:

MAX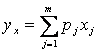

Subordinatamente ai vincoli:

( i = 1 , 2 , .. , n )

x_i (j = 1, 2, ..., m

Chiameremo questo problema primale. Il problema duale corrispondente ad esse è:

MIN

Subordinatamente ai vincoli :

( j = 1 , 2 , .. , m )

z_i ( i = 1 , 2 , .. , n )

Cioè il duale di un problema di P.L. si ottiene dal primale:

sostituendo al problema di massimizzazione in m variabili ed n vincoli un problema di minimizzazione in n variabili ed m vincoli;

scambiando i coefficienti della funzione obbiettivo con i termini dei vincoli;

scambiando righe con colonne nella matrice dei coefficienti dei vincoli;

cambiando il verso delle disuguaglianze di vincolo.

Dunque c'è una variabile duale per ogni vincolo primale ed un vincolo duale per ogni variabile primale; per quanto concerne i vincoli i coefficienti del vincolo j-esimo del problema duale sono i coefficienti con i quali compare la variabile x_j nei vincoli del primale e viceversa.

Sulla dualità di un problema di P.L. valgono alcuni teoremi fondamentali che sono:

Teorema 1. Esiste il duale di qualsiasi problema di programmazione lineare.

Teorema 2. Il duale del duale è il primale.

Teorema 3. I valori che può assumere la funzione obiettivo in un problemadi massimo sono minori o uguali a quelli che può assumere la funzione obbiettivo del corrispondente problema di minimo duale.

Teorema 4.Se:

x^*=(x^*_1, x^*_1,..., x^*_m)

è la soluzione ottimale di un problema primale e:

z^*=(z^*_1, z^*_1,..., z^*_n)

è la soluzione ottimale del duale, risulta:

y_x (x^*) = y_z (z^*)

Cioè : i valori della funzione obiettivo del primale e del duale, calcolati nelle rispettive soluzioni ottime,coincidono.