IL CALCOLO INTEGRALE

matematica

IL CALCOLO INTEGRALE.

L'INTERALE DEFINITO :

TEOREMA :

Sia y = f(x) una funzione continua nell'intervallo (a ;b) ; esiste allora ed è 949c23j finito il limite per n dell'area del plurirettangolo inscritto e dell'area del plurirettangolo circoscritto. Tali limiti coincidono ed il loro valore comune è detto integrale definito della funzione nell'intervallo (a;b). Esso esprime quindi la misura dell'area del trapezoide di base AB e si scrive :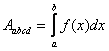

PROPRIETA':

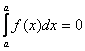
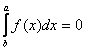   se a < b

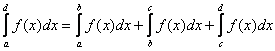
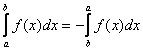  se a > b

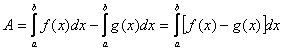
V =

TEOREMA DI TORRICELLI - BARROW:

Data la funzione y = f(x) continua nell'intervallo (a;b), la funzione integrale F(x) = 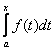  è derivabile in (a;b) e F'(x) = f(x) e F(0) = 0.

Interpretazione del Teorema: Se la funzione y = f(x) è continua nell'intervallo (a;b), allora esiste una

primitiva della funzione integranda y = f(x) ed essa è la funzione

integrale F(x) cioè F'(x) = f(x).

L'INTEGRALE INDEFINITO:

DEFINIZIONE:

Si dice integrale indefinito di una funzione y = f(x), e si indica con il simbolo  la totalità delle primitive della f(x).

TEOREMA:

Se una funzione y = f(x) ammette in un intervallo I una primitiva, allora ne ammette infinite che si ottengono tutte aggiungendo alla F(x) una qualunque costante c.

PROPRIETA':

1.

2.

IMPORTANTE:

Il differenziale dell'integrale di una funzione è uguale alla funzione stessa:

F'(x) = f(x)

f(x) =

INTEGRALI INDEFINITI IMMEDIATI:

1. per

2.| + c

3.

4.

5.

6.

INTEGRALI INDEFINITI IMMEDIATI GENERALIZZATI :

1.

2.

3.

4.