LA PROBABILITA'

matematica

LA PROBABILITA'

La probabilità è una funzione che associa un numero ad un evento.

Assiomi della probabilità

1.     P = 0 evento impossibile

151c23b    P = 1 evento certo

2. 

151c23b     se gli eventi sono incompatibili

3. 

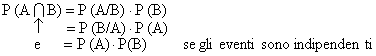
151c23b    Due eventi sono indipendenti quando la P di verificarsi dell'uno

151c23b 151c23b non influisce su quella dell'altro.

4. 

5. almeno 1 = 1 - nessuno ( 1 - la P che l'evento non avvenga)

6. 

151c23b

Formule di Bayes (da utilizzare tutte le volte che "torno indietro", ossia quando parto dal dato

151c23b     finale)

VARIABILI

Variabile discreta : posseggo un numero finito di valori

F (x) = funzione di distribuzione

media 

varianza 

s.q.m.

moda = valore MAX

mediana () = valore che divide la densità di probabilità in due parti di uguale area

151c23b F (x) =

Variabile continua : posseggo un numero infinito di valori

   

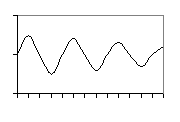
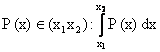
F (x) =

s.q.m.  

moda = valore MAX

F (x) =

Modelli di variabili discrete

Binomiale: evento ripetuto n volte

K successi

P = probabilità di successo

1 - p = probabilità di insuccesso

con = coefficiente binomiale

di cui  

Poissoniana: da utilizzare se n è molto grande e P è molto piccolo si usa quando si hanno eventi

151c23b   Rari.

  con = nP

di cui  

Modelli di variabili continue

Uniforme

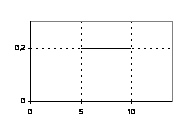I numeri sono puramente di esempio. In questo caso a = 5, b = 10

P (x) =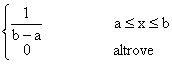

di cui  

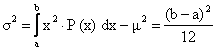
normale

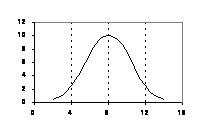I numeri sono puramente di esempio. In questo caso

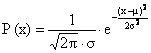con

? (non esiste alcuna formula per risolverlo)

Devo trovare un altro metodo per risolvere la legge.

Applico alla formula una trasformazione in cui

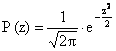
(distribuzione normale standardizzata)

La curva normale con cambia e diventa la curva normale standardizzata:

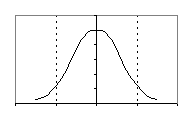In questo caso: , il massimo della gaussiana è in O (0,y)

Se voglio risolvere un problema con la variabile normale calcolo , dove sono note e x è ricavabile dal problema. A questo punto utilizzo la tabella per calcolare l'area sottesa alla gaussiana compresa tra le due x.

Variabili statistiche

Le variabili probabili studiano i fenomeni teoricamente.

Le variabili statistiche studiano i fenomeni osservati.

Legge Grandi Numeri

Se N (numero tentativi) è molto grande la frequenza relativa tende ad assumere il valore di P

F (x) = funzione cumulativa di frequenza

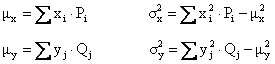
covarianza:

coefficiente di correlazione lineare:

indipendenza stocastica: