GEOMETRIA ANALITICA PIANA - IL RIFERIMENTO CARTESIANO

L'equazione di una retta è: y = mx + q dove m è il coefficiente angolare e q è il termine noto.

PUNTO MEDIO DI UN SEGMENTO

Secondo il teorema di Talete, per trovare il punto medio "M" del segmento AB si usa la formula:

x₁ + x₂ y₁ + y₂

x_M y_M =

2 2

DISTANZA TRA 2 PUNTI

Secondo il teorema di Pitagora, per trovare la distanza "d" tra 2 punti si usa la formula:

d (A, B) = \ (x₂ - x₁)² + (y₂ - y₁)²

ASSE DI UN SEGMENTO

L'asse del segmento AB, con A (a₁, a₂) e B (b₁, b₂), è il luogo dei punti P (x, y) del piano equidistanti da A e da B:

\ (x - a₁)² + (y - a₂)² = \ (x - b₁)² + (y - b₂)²

CIRCONFERENZA NEL PIANO

La formula della distanza tra 2 punti del piano ci permette di ricavare l'equazione della circonferenza. La circonferenza è il luogo dei punti P(x, y) detto centro della circonferenza:

x² + y² + ax + bx + c = 0

RETTA NEL PIANO

L'equazione della retta passante per 1 punto:

y - y₀ = m (x - x₀)

L'equazione della retta passante per 2 punti:

y - y₁ y₂ - y₁

=

x - x₁ x₂ - x₁

Per ottenere l'equazione della retta è sufficiente conoscere il valore di m, che è la costante detta coefficiente angolare della retta e ne esprime l'inclinazione. m si trova con la formula:

y₂ - y₁

m =

x₂ - x₁

L'equazione y = mx + q si chiama equazione esplicita della retta; la costante q viene anche detta intercetta.

DISTANZA DI UN PUNTO DA UNA RETTA

Dato un punto P e una retta r di equazione ax + by + c = 0, la formula della distanza di 2 punti è:

| ax₀ + by₀ + c|

d (P, r)

\ a² + b²

ELLISSE

Ellisse: è il luogo geometrico per i quali è costante la somma delle distanze da 2 punti fissi chiamati fuochi.

I punti d'intersezione fra l'ellisse e gli assi si chiamano vertici, rispettivamente quelli sull'asse x A₁ e A₂; quelli sull'asse y B₁ e B₂.

Le distanze di tali vertici dall'origine si chiamano semiassi.

Se l'ellisse si trova posizionato coi i fuochi sull'asse x la distanza A₁O = A₂O = a è detta semiasse maggiore, mentre B₁O = B₂O = b è detta semiasse minore.

Equazione dell'ellisse:

x² y²

= 1

a² b²

Coordinate dei 2 fuochi:

Si indicano con C;0 = C;0 = c dove:

c = \ a² - b²

Eccentricità dell'ellisse:

L'eccentricità dell'ellisse e descrive la rotondità dell'ellisse stessa; è (compreso tra) 0 ≤ e e si calcola attraverso il rapporto:

c

e =

a

Se a > b → i fuochi si trovano sull'asse x; vale la relazione: b² = a² - c²

Se a < b → i fuochi si trovano sull'asse y; vale la relazione: b² = a² + c²

Le coordinate dei vertici sono:  Le coordinate dei fuochi sono:

A₁ (- b ; 0) A₂ (b ; 0) F₁ (0 ; - c)

B₁ ( - a) B₂ (0 ; a) F₂ (0 ; c)

Il semiasse maggiore a si trova sull'asse y

Il semiasse minore b si trova sull'asse x

IPERBOLE

Iperbole: è il luogo geometrico per i quali è costante la differenza delle distanze da 2 punti fissi chiamati fuochi.

Equazione dell'iperbole:

x² y²

= 1

a² b²

L'iperbole interseca l'asse x nei punti di coordinate (a, 0) e (-a, 0), detti vertici dell'iperbole, mentre non ha intersezioni con l'asse y

b

Asintoti dell'iperbole y =± x

a

Eccentricità dell'iperbole:

L'eccentricità dell'iperbole e e > 1 e si calcola attraverso il rapporto:

c

e =

a

Equazione dell'iperbole se i fuochi si trovano sull'asse y:

y² x²

= 1

b² a²

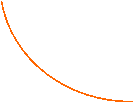
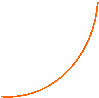
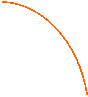
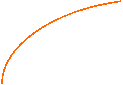
Asintoti dell'iperbole equilatera: y =± x    (cioè con le bisettrici).

Se notiamo l'iperbole equilatera di 45° l'iperbole equilatera riferita ai propri asintoti di equazione:

k

y =

x

h < 0 h > 0

k - k

PARABOLA

La parabola è una funzione quadratica, detta così perché la x ha esponente 2. La funzione è:

y ⁼ ax² + bx + c

Se ax² è positivo la concavità è rivolta verso l'alto;

Se ax² è negativo la concavità è rivolta verso il basso.

La formula della parabola è:

- b ± b² - 4ac

x_1/2

2a

a > 0 xЄR

sempre

a < 0