|
|
| |
Disequazioni
Le disequazioni sono diseguaglianze fra due espressioni e possono essere numeriche se compaiono solo numeri, letterali se compaiono lettere dette incognite, fratte, se al denominatore compaiono delle incognite e possono risultare:
Rappresentazioni grafiche
I risultati delle disequazioni si indicano sempre ponendo il valore ottenuto in una retta per esempio
1-3x < 2x-6
-5x <7
5x > 7
x > 7/5
Il grafico vuole significare che x può assumere infiniti valori purché questi siano maggiori di 7/5
Per le disequazioni indeterminate, almeno che non vengano fornite delle condizioni per cui certe lettere saranno maggiori, uguali o minori di certi valori, (per esempio A=0 B<2 C>3 ecc) non conoscendo i valori delle lettere non sarà possibile fare un grafico e si scriverà accanto alla soluzione "disequazione indeterminata"
Per le disequazioni impossibili si farà il grafico indicando la disequazione come "impossibile" o "non accettata" senza riportare risultati per esempio:
5-6 > 8
-1 >8
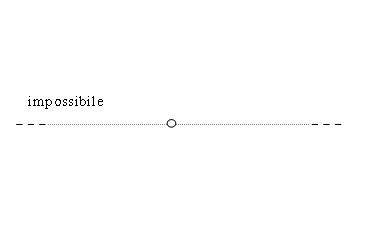
Si indica nel grafico che la disequazione è impossibile lasciando il cerchietto all'interno bianco e riportando la scritta "impossibile" oppure "non accettata"
Cambi si segno
Se si applica il secondo principio di equivalenza nelle disequazioni e si moltiplica o divide per un valore negativo, il senso del simbolo di disuguaglianza viene invertito:
-x < 2
Moltiplicato o diviso per -1 diventa:
x > -2
Disequazioni Fratte
1. Ricordiamo che una disequazione si dice fratta se contiene l'incognita anche al denominatore di qualche frazione. Esempio:
![]()
2. Per risolvere una disequazione fratta si deve portare tutto al primo membro e ridurre ad una frazione unica. Si arriverà ad espressioni del tipo
![]()
3. Si deve prendere separatamente il numeratore e il denominatore della disequazione, e porli l'uno maggiore di 0 se hanno segno concordi come nell'esempio, ( nel caso avessero segni discordi sarebbe stato da porre a scelta uno maggiore e uno minore di 0)
3-x > 0 -x > -3 x < 3
e
x-1 > 0 x > 1
La precedente operazione a volte può essere rappresentata sottoforma di sistema e può apparire cosi
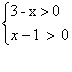
4. Riportare dunque i risultati in un grafico:
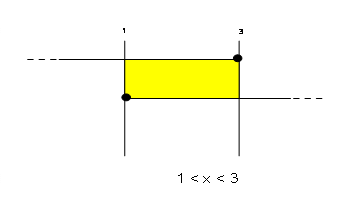
Sistemi di disequazioni
Quando si ha un sistema di disequazioni si deve risolvere le disequazioni date nel sistema separatamente, in seguito le soluzioni ottenute dalle due disequazioni si rimettono a sistema e in seguito si traccia il grafico delle dei risultati delle disequazioni. Esempio :
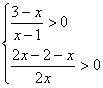
Soluzioni prima disequazione
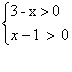
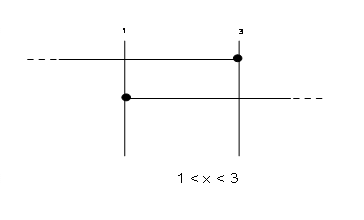
Soluzioni seconda disequazione
![]()
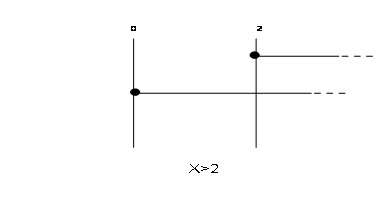
Si rimettono le soluzioni a sistema:
![]()
Si mettono a sistema le soluzioni :
(pag seguente)
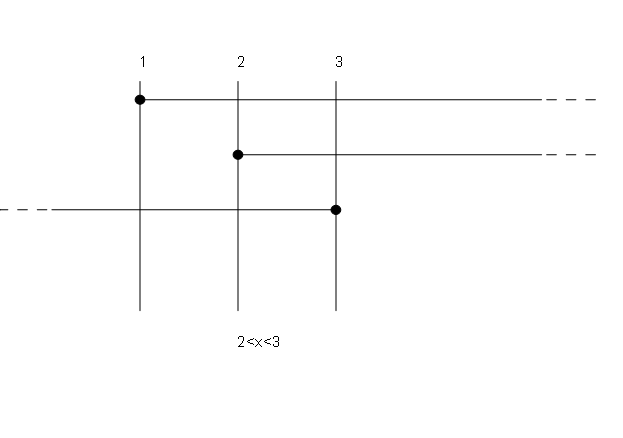
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025