 |  | |
|
| | |
|
| |
Cinematica
La Cinematica è quella branca della Fisica che studia il moto dei corpi, cioè la velocità e la posizione di un punto materiale in funzione del tempo.
Analizzare un punto materiale significa studiare il moto di un corpo senza preoccuparci della sua struttura, ma identificandolo con un vettore r
Per identificare la posizione di un punto materiale bisogna intanto
scegliere un sistema di riferimento.
Y
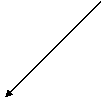X
Z Piano ortogonale Cartesiano
Per caratterizzare il moto di un corpo bisogna quindi identificare la posizione rispetto al tempo t con una funzione detta legge oraria:
legge oraria r(t)
d r(t) [m/sec] d t
Anche la velocità v è un vettore in funzione del
tempo:
velocità v(t)=
La Posizione si misura in [m].
d v(t) [m/sec2] d t
Possiamo anche definire un'altra grandezza che
ci permette di scrivere la legge oraria, cioè l'accelerazione, intesa come
variazione di velocità in un intervallo di tempo
accelerazione a(t) =
Con Traiettoria invece si intende il luogo dei punti individuati dalla particella lungo il suo percorso.
Moti unidimensionali
Con moto unidimensionale si intende un moto che si svolge solamente su una dimensione. Quindi prendendo come asse di riferimento quello delle ascisse potrò scrivere X(t).
Moto rettilineo Uniforme
Il moto rettilineo uniforme è quel moto caratterizzato da accelerazione nulla, ossia non varia la velocità 121e44b nel tempo. Quindi Vi e Vm coincidono.
a
Quindi avremo:
t o
a (t) = O
x vo v
t o
V (t) = Vo (costante)
x (t)
La posizione
rispetto al tempo si trova da:
x
(t) - x (to) [m/sec] t - to x
(to) + Vo (t - to) [m/sec] t - to o t
Vo = x(t) =
Moto Uniformemente Accelerato
d v(t)
d t
y
a (t) = a am = ai a = am = v
(t) - v (to)
to t a = t - to
t
- to
v (t) -
v (to)
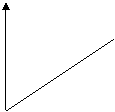
to t
v (t) = v (to) + a (t - to) [1]
Per trovare la posizione x (t) invece calcolando l'area di questo grafico, la cui equazione è la [1], troveremo lo spazio percorso tra t e to:
x (t) = x (to) + v (to) (t - to) + ½ [(v - vo) (t - to)] Moltiplicando e dividendo per (t - to) avremo
x (t) = x(to) + v (to) (t - to) + ½ [(v - vo) (t - to)2] x (t) = x (to) + v (to) (t - to) + ½ a (t - to)2
(t - to)
a (t) = a
v (t) = v (to) + a (t - to)
x (t) = x (to) + v (to) (t - to) + ½ a (t -to)2
(t - to) = v (t) - v (to)
a
x (t) - x (to) = v (to) [v (t) - v (to)] + ½ a ((v (t) - v (to))2
a a2
1/a [- v (to) + ½ vt2
+ ½ vto2] =
x (t) - x (to) = 1/2a [v (t)2 - v (to)2] v2
(t) = v2 (to) + 2a [x (t) - x (to)]
Moti Bidimensionali
y
Con Moto bidimensionale si intende un moto che
si svolge su due dimensioni viene quindi anche modificato il sistema di
riferimento rispetto ai moti unidimensionali.
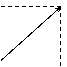
y (t)
Per rappresentare il moto viene usato un
vettore:
r (t)
x x (t)
Quindi l'accellerazione e la velocità si possono scomporre
Secondo le due componenti dell'asse delle x e delle y:
v (t) = vx (t) i + vy (t) j
v (t) = lim r (t + Dt) - r (t) lim [ (x (t) + Dt) i + y(t+Dt) - y (t)] j = d x(t) i + d y(t) j
Dt o Dt t o Dt Dt Dt Dt
v = vx (t) i + vy (t) j = d x(t) i + d y(t) j
d t d t
a (t) = d vx(t) i + d vy(t) j
dt dt
Moto Parabolico
Il moto parabolico è il moto di tutti gli oggetti che si muovono e sono soggetti a una accelerazione costante in modulo e verso.
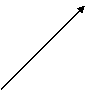
Y
hmax
Vy
V
Vx x
Sull'asse y l'accelerazione è costante, rivolta verso il basso ed è uguale alla forza di gravità g.
A= -g j
Scomponiamo ora la velocità, l'accelerazione e la posizione del corpo lungo l'asse x e l'asse y.
Sull'asse y avremo:
ay = -g Vy (t) = Voy (-g t) [1] y (t) = Voy
t - ½ gt2 [2] 
Sull'asse x avremo:
ax
Vx(t) = Vo cosJ = Vx
x (t) = Vo cosJ t = Vx t [3]
Vogliamo ora trovare l'altezza massima che l'oggetto raggiunge. Dalla [1] il tempo t è:
t = Voy
g
Se sostituiamo il tempo trovato nella [2], avremo:
Ymax (t) = Voy Voy -
½ g Voy2 Voy2
- ½ Voy2
g g2 g g
Ymax = ½ Voy2
g
Il punto x nelle ascisse in cui l'oggetto è al massimo dell'altezza è:
x = Vox Voy
g
La Gittata è la distanza massima sull'asse delle x nel momento in cui l'oggetto tocca il suolo. Essendo inquestopunto y=0,possiamo trovare il tempo dall'equazione dalla [2] e sostituirla nella[3].
y (t) = Voy t - ½ gt2 0 = Voy
t - ½ gt2 t = 2 Voy
g
x (t) = Vox t x (t) = 2 Vox Voy [Gittata]
g
La Traiettoria invece è il luogo dei punti individuato dalla particella lungo il suo percorso
t = x _ y (t) = Voy
x - ½ g __x2_ y (t) = V
sen J x - ½
g x2______
Vox Vox Vox2 V cos J V2 cos2 J
Y (t) = tg J x - ½ g______ Eq. della Traiettoria
V2 cos2 J
Moto Circolare Uniforme
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
