|
|
| |
Alcuni giochi proposti nelle precedenti olimpiadi della matematica
Cento quadrati?
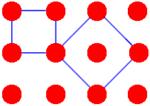
Includendo i due quadrati già disegnati, quanti quadrati, che abbiano le loro estremità comprese fra i dodici punti del disegno qui accanto, possiamo al massimo disegnare?
|
|
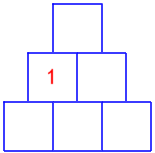
La piccola piramide
Completare la piramide qui accanto con i numeri da 2 a 6 in modo tale che, con esclusione della fila in basso, un numero sia sempre uguale alla differenza dei due numeri immediatamente sotto.
Il collezionista
Tom colleziona farfalle. Tiene i suoi esemplari in undici scatole. Ciascuna delle undici scatole contiene almeno una
farfalla. Otto di queste undici scatole ne contengono ciascuna almeno due, sei ne contengono ciascuna almeno quattro e due ne contengono esattamente cinque ciascuna. Di quante farfalle , come minimo, si compone la collezione di Tom?
La raccolta dei funghi
Andrea, Beatrice, Chiara e Damiano sono andati a raccogliere i funghi e sono tornati con i loro cesti riempiti di porcini. Damiano ne aveva più di Chiara, ma A Andrea ne aveva meno di Chiara.Andrea e Beatrice messi insieme ne avevano la stessa quantità di Chiara e Damiano messi insieme.Chi ne aveva di più? Chi ne aveva di meno?
Il podere di papà Quasimodo
Papà Quasimodo possiede un podere della forma disegnata qui accanto. Quattro bellissime querce sono piantate in questo podere. Quasimodo decide di dividere il suo podere, per i suoi quattro i figli, in quattro porzioni della stessa forma e della stessa superficie, ogni porzione dovendo contenere una delle querce.
Aiutate Quasimodo a fare la ripartizione, disegnando sulla mappa il confine delle quattro porzioni.
Il numero a sette cifre
In un numero a 7 cifre formato delle cifre 1, 2, 3, 4, 5, 6 e 7 presenti ciascuna una volta, la somma delle due cifre consecutive è sempre uguale o alla somma delle due prime cifre, oppure alla somma delle due ultime. Trovate questo numero. Si richiede solo una soluzione.
Il piccolo quoziente
Si divide un numero a due cifre per la somma
delle sue due cifre. Esempio: 23 : (2+3) = 23 : 5 = 4.6.
Qual'è il più piccolo quoziente
ottenibile? Se necessario, arrotondare al millesimo.
8) Il quadrato latino
In un quadrato di 5 caselle per 5 caselle, si scrivono i numeri 1, 2, 3, 4, 5, in modo tale che:
su ogni riga e su ogni colonna appaiano ciascuno dei cinque numeri
il quadro riempito sia simmetrico rispetto ad una delle sue diagonali.
Quali sono il valore minimo ed il valore massimo della somma dei 9 numeri scritti nelle due diagonali del quadrato?
Una bella torta
E' il compleanno di Matilde. I suoi due amici
Mattia e Giacomo le hanno portato una bellissima torta quadrata. Con una
coltellata diritta, Mattia taglia la torta in due pezzi, poi, con una seconda
coltellata diritta, divide uno dei pezzi in due. Risultano tre belle fette, la
più grossa è ovviamente destinata a Matilde.
Matilde prende allora il suo goniometro (lavabile) e misura tutti gli angoli
delle tre fette. Somma tutte queste misure con la sua super calcolatrice
(resistente all'acqua e allo yogurt).
Qual'è il valore minimo che può trovare? Dare la risposta in gradi.
Le due sorelle
Le due sorelle Barbara e Monica festeggiano oggi il loro compleanno comune, perché sono nate lo stesso giorno dello stesso mese. Barbara è più giovane di due anni. A una domanda sulla sua età, Monica risponde:
"Barbara è molto giovane, perché conta meno anni di quanti ne avevamo insieme nove anni fa. Per quello che mi riguarda sono vecchia, perché conto più anni di quanti ne avevamo insieme nove anni fa."
Qual'è l'età di Barbara?
Il grande stravolgimento
In una serie numerica, si ha il diritto di effettuare l'operazione seguente: si scelgono più elementi che si seguono (al minimo due elementi, al massimo la serie intera) e si inverte l'ordine di queste elementi, lasciando invariato l'eventuale resto della serie.
Esempio: 8, 1, 6, 2, 3, 9, 4, 7 risulta 8, 1, 6, 4, 9, 3, 2, 7.
In quante operazioni, al minimo, si può passare dalla serie 8, 9, 3, 4, 5, 6, 7, 1, 2 alla serie 1, 2, 3, 4, 5, 6, 7, 8, 9?
Gioco del cavaliere
Un cavaliere di scacchi si trova inizialmente sulla casella B4 di una scacchiera di 8 caselle per 7. Essendo su una casella qualunque, può effettuare uno e uno solo dei quattro movimenti indicati sulla figura (a condizione che sia realizzabile senza uscire dalla scacchiera).
I due giocatori spostano il cavaliere alternativamente finché uno dei giocatori non possa più giocare. L'ultimo giocatore che ha potuto giocare è dichiarato vincitore.
Giocate per primo. Sbarrate sulla scheda-risposta la o le caselle corrispondenti al primo movimento che fate per essere sicuro di vincere, qualinque mossa faccia il vostro avversario (ogni movimento è indicato dal suo numero sulla figura qui sopra).
Rispondete 0 soluzioni se pensate che il secondo giocatore vincerà, qualunque mossa voi facciate.
Maxi-freccette
Dopo un torneo di freccette aspramente disputato, Adriano, Bernardo, Carlo, Daniele, Emilio e Francesco si staccano dal gruppo dei concorrenti: sono pari.
La giuria decide un ultimo spareggio: ogni concorrente dovrà lanciare sei freccette da una distanza diversa; il totale del punteggio deciderà il vincitore.
Alla fine dei lanci tutte le freccette hanno raggiunto il bersaglio, i concorrenti hanno realizzato, ad ogni lancio, un punteggio pari almeno al precedente, gli elenchi dei punteggi dei sei concorrenti sono tutti diversi e la giuria constata con stupore che i sei concorrenti hanno tutti realizzato un totale di 97 punti!
Se soltanto i tre migliori punteggi fossero presi in considerazione, ci sarebbero ancora tre concorrenti alla pari: Carlo, Daniele ed Emilio. La gara è già durata abbastanza. La giuria decide allora di classificare i candidati secondo il prodotto dei sei risultati realizzati, assegnando la vittoria a chi totalizza il valore più alto.
A risultati pubblicati, si puo' notare che:
nessun concorrente ha ottenuto tre volte lo stesso punteggio
Bernardo e Adriano sarebbero stati alla pari se si fossero sommati i quattro migliori punteggi
Adriano non ha mai realizzato 30
Carlo ha ottenuto una volta il punteggio più basso possibile
Daniele, il perdente, ha pure colpito una volta il centro del bersaglio, mentre Francesco, dichiarato vincitore, non l'ha mai colpito!
Fornire il prodotto dei punteggi ottenuti dai concorrenti (in migliaia).
La serie periodica
Un calcolatore esegue il programma seguente: Se si introducono due cifre a e b, le scrive, poi scrive la cifra delle unità della somma a+b. Continua poi scrivendo ad ogni tappa la cifra delle unità della somma dei due numeri precedenti. Giuseppe, dopo aver introdotto le due prime cifre tali che a sia minore b, constata che il calcolatore ottiene una serie di quattro cifre che si ripete all'infinito.
Quali erano le due cifre introdotte da Giuseppe?
Il gioco del polinomio
Un professore propone ai suoi alunni di
trovare la radice intera d'un polinomio P a coefficienti interi.
Uo alla volta, gli alunni propongono un numero a, e il professore annuncia il
valore di P(a) e la posizione di a rispetto alla radice intera.
Giuliano: "7"
Il professore: "P(7)=77 e la radice intera è maggiore di 7"
Bernardo: "..." (non udibile dal resto della classe)
Il professore: "P(...)=85 e la radice intera è maggiore del numero proposto".
Qual'è il valore della radice intera?
I due dadi
Si hanno a disposizione due dadi cubici che
portano sulle loro facce dei numeri interi da 1 a 12, non necessariamente tutti
diversi. Si lanciano questi due dadi e si somma il numero di punti indicati. Si
possono così ottenere tutti i numeri da 2 a 19 con la stessa probabilità.
Quali numeri portano le facce dei due dadi?
Per ogni dado, si scrivano questi numeri in ordine crescente. Attenzione! I giochi dal 14 al 16 possono avere più soluzioni.
Soluzioni
Cento quadrati
Numero massimo di quadrati: 10.
2) La piccola piramide
La soluzione è quella mostrata nella figura.
3) Il collezionista
Il numero delle farfalle è 33.
4) La raccolta dei funghi
Beatrice ne aveva di più, Andrea ne aveva di meno.
Inizio C2, L1, L2, GP
5) Il podere di papà Quasimodo
La soluzione è quella mostrata nella figura.
6) Il numero a 7 cifre
Soluzioni: 1634527, 1726354, 4352617, 4536271, 7162534, 7254361.
7) Il piccolo quoziente
Il più piccolo quoziente è 1.9.
8) Il quadrato latino
Il minimo è 19, il massimo 35.
Fine C1 9) Una bella torta
Il minimo è 540 gradi.
10) Le due sorelle
L'età di Barbara è 17 anni.
Fine C2 11) Il grande stravolgimento
Numero minimo di operazioni: 3.
12) Il gioco del cavaliere
Le mosse sono 2 e 4.
13) Maxi-freccette
Adriano 1125, Bernardo 2025, Carlo 135, Daniele 75, Emilio 180, Francesco 2700.
Fine L1 14) La serie periodica
Le due cifre 2 e 6, oppure le due cifre 6 e 8.
15) Il gioco del polinomio
I valori delle radici intere sono 8, 14 e 84.
Fine L2 e GP 16) I due dadi
Sul dado 1: 1 2 3 10 11 12, sul dado 2: 1 1 4 4 7 7.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025