II ESPERIENZA DI MATEMATICA - Metodo di bisezione

matematica

II ESPERIENZA DI MATEMATICA

Metodo di bisezione

Il metodo di bisezione consente di ricavare le radici di un'equazione.

Per prima cosa bisogna separare le r 959h77j adici dell'equazione, cioè ricavare gli intervalli in cui cade una e una sola radice (o soluzione).

Es.:  Se f(x) non si può risolvere con i metodi tradizionali, allora utilizzo il metodo di bisezione.

Rappresento y=f(x) e controllo dove la funzione taglia l'asse x.

Trovo i punti ad esempi a e b, quindi calcolo f(a) ed f(b).

Successivamente controllo se agli estremi dell'intervallo la funzione cambia segno, in caso contrario, ho sbagliato il valore della radice.

Per fare questa verifica, bisogna sottrarre il valore di f(a) a quello di f(b) e vedere se è minore di 0.

Dopo aver fatto questo, bisogna costruire una tabella:

In C si mette il valore del punto medio tra a e b calcolato con la formula: (A+B)/2

Se f (c ) =0 allora c è la radice dell'equazione.

Se f(c )>0 allora la radice cade tra [c;a].

Se f(c )<0 la radice cade tra [a;c].

Si procede così fino a che l'errore assoluto è minore di (Bn-An)/2. Dove n è il numero di intervalli.

E' un metodo molto semplice ma molto lungo perché il procedimento converge sempre, ma bisogna eseguire numerose operazione prima di arrivare alla stima esatta della radice.

Il procedimento è stato svolto in linguaggio C++, ma non convergeva se l'errore era minore di 10^-5, quindi è stato messo un errore minore di 10^-4. Il metodo converge trovando le 2 soluzioni dell'equazione, cioè:

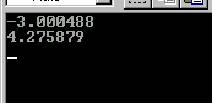
Le radici dell'equazione sono state separate in questo modo:

Equazione: x⁴-x³-256

Radici:   y=x³

y=x⁴-256