Misura del momento di inerzia di un disco

Ri = (0,010 0,001)m e raggio esterno Re = (0,050 0,001)m;

un personal computer  collegato ad un sensore di rotazione che analizza e acquisisce i dati e dà in output i valori dell'accelerazione angolare;

un programma per la registrazione della pozione angolare  q (t), e il calcolo della velocità angolare w (t) = dq/dt, e dell'accelerazione angolare a (t)= dw/dt;

diverse masse m;

filo inestensibile collegato alla piattaforma;

un calibro con sensibilità ( 0,001)m ;

3. Procedimento: si imposta il programma in modo che misuri 828d35i la posizione angolare; nelle opzioni alla voce Divisioni/Rotazioni  scegliamo 1440 tacche utilizzate in ogni giro per aumentare la precisione; impostiamo la frequenza a 100 Hz.

Ogni massa viene agganciata al filo; si aziona il software nella modalità di registrazione dati e si lascia cadere la massa verticalmente. Questa cadrà fin quando non si raggiungerà l'estensione massima del filo. A quel punto si interromperà la registrazione dei dati. Sfruttando il software e utilizzando le coppie di dati formate dalle posizioni angolari e dagli intervalli di tempo, si visualizza un grafico che si approssima, con una linea di tendenza, a un  ramo di parabola. Il software fornisce l'equazione di tale parabola da cui si ricava il coefficiente del termine di secondo grado che, moltiplicato per due, dà il valore dell'accelerazione angolare. Il processo viene ripetuto altre 4 volte; dopo si calcola il valore medio delle cinque accelerazioni angolari ottenute.

Il procedimento sopra descritto viene ripetuto per ogni massa.

Di seguito sono riportati i dati delle accelerazioni angolari e dei loro valor medi. 

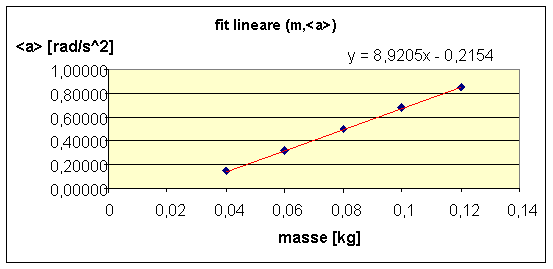
Dopo si rappresenterà su un grafico la relazione  che intercorre fra i valori medi delle accelerazioni angolari e le rispettive masse. Si aggiungerà una linea di tendenza e dall'equazione risultante si otterranno i coefficienti necessari per calcolare il momento d'inerzia del sistema senza disco.

Consideriamo il sistema piattaforma :

M  = momento della forza attiva

T   = tensione del filo

Mf = momento frenante che si oppone al moto

Ip  = momento d'inerzia della piattaforma

a = accelerazione angolare

g  = accelerazione di gravità

r   = raggio della puleggia = (0,012 0,001)m

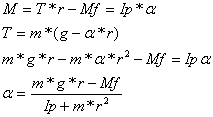
La dipendenza non è lineare ma si può fare un'approssimazione

Quindi:

Ora abbiamo una dipendenza lineare fra a e m e la relazione qui sopra è analoga all'equazione ottenuta dal fit:

Il momento d'inerzia del sistema senza disco è (0,013)k g*m^2.

Ripetiamo l'intero procedimento precedente ponendo il disco sopra il sistema rotante a una distanza l=0,2 m  dal baricentro del sistema, ottenendo così i seguenti dati e il seguente momento d'inerzia del sistema con disco:

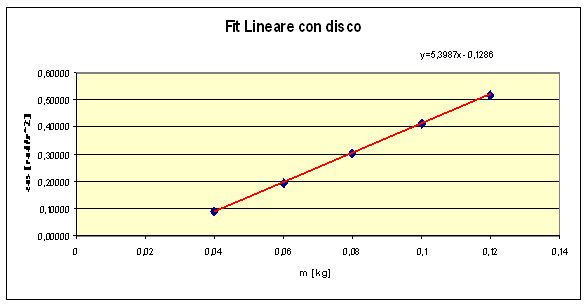
Si calcola ora il momento d'inerzia del sistema con disco ()

Si calcola così il momento d'inerzia del disco sottraendo al momento del sistema con disco il momento del sistema senza disco:

Si calcola poi il momento d'inerzia teorico () del disco tramite l'applicazione del teorema di Steiner:

4. Conclusioni: il valore sperimentale del momento di inerzia del disco e quello teorico sono praticamente uguali. Non si sono potuti calcolare gli errori corrispondenti perché le varie accelerazioni angolari riportate nei grafici sono state ottenute da equazioni di 2° grado di fit polinomiali per le quali non si conosce l'appropriato metodo dei minimi quadrati. Una causa d'errore è costituita dalle forze d'attrito che, non essendo nulle, hanno una certa influenza.