OBIETTIVO:

Studio della capacità di un condensatore ed analisi della carica e scarica.

STRUMENTI :

N° 1 Basetta;

N°1 Commutatore, ovvero un interruttore con 3 posizioni possibili per inserire il generatore, eliminarlo e lasciarlo aperto;

N° 1 Generatore di forza elettromotrice e continua;

N° 1 Resistenza da 5.6 kW con tolleranza del 5%;

N° 1 Condensatore da 2.2 mF ± 20%;

N° 1 Condensatore da 1 mF± 20%;

N° 1 Cronometro digitale;

N° 1 Voltmetro digitale.

INTRODUZIONE TEORICA :

Sarà fondamentale nello studio dell'esperienza la conoscenza del circuito indicato in figura seguente:

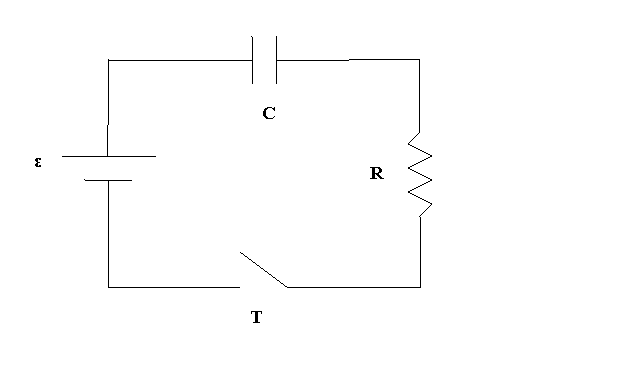
Esso è costituito da un generatore di forza elettromotrice, un condensatore ed una resistenza. Alla chiusura dell'interruttore (T in figura), il generatore inizia a prelevare cariche dall'armatura connessa al polo negativo per portarle all'armatura collegata al polo positivo in modo tale che sulle armature del condensatore compaiano le cariche +q e -q.

Il processo continua fino a quando la carica del condensatore raggiunge il valore massimo q_o = C*e. In un generico istante t valgono le relazioni:

ove si è posto:

Mettendo insieme le relazioni appena scritte, otteniamo:

Integrando tra l'istante t= 0 e l'istante generico t in corrispondenza dei quali sulle armature del condensatore ha le cariche q= 0 e q, otteniamo:

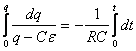
che porta, una volta risolta, a:

Queste ultime due equazioni regolano la carica elettrica e la differenze di potenziale del condensatore con il tempo ed è evidente che entrambe le grandezze citate dipendono dalla costante di tempo t = RC.

Relativamente alle grandezze da misurare, in fase di carica conviene misurare la tensione ai capi del condensatore e poi calcolare quella ai capi della resistenza. Infatti poi sarà possibile linearizzare la curva rappresentando in scala semilogaritmica (t,V_R) poiché:

Se in un determinato istante e dopo aver fatto caricare il condensatore (in parte o totalmente) si esclude il generatore, questo inizierà a perdere la carica posseduta che sarà dissipata nella resistenza.

Nell'istante generico t la differenza di potenziale V_C ai capi del condensatore è uguale a quella V_R ai capi della resistenza quindi valgono le relazioni:

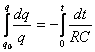
e passando ad integrare:

Risolvendo quest'ultimo integrale ottiene:

In fase di scarica conviene misurare la tensione ai capi del condensatore:

Infatti è possibile cambiando variabili linearizzare la curva rappresentandola in scala semilogaritmica (t,V_C) poiché:

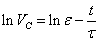
Dalle relazioni appena esposte si evince che la carica e la differenza di potenziale decrescono esponenzialmente nel tempo con una rapidità caratterizzata dalla costante di tempo t = RC.

PROCEDIMENTO :

Si è proceduto a realizzare il circuito indicato in figura seguente:

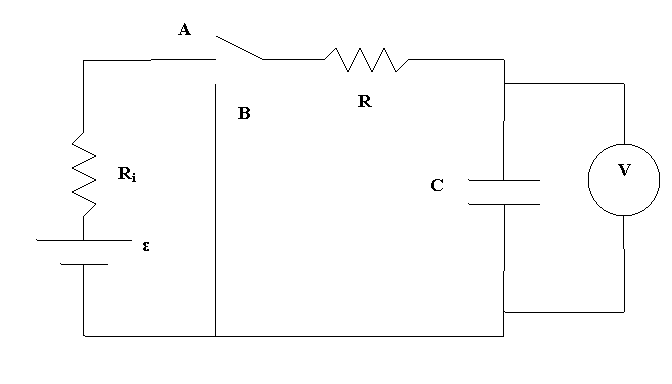
dotato di un commutatore al posto dell'interruttore in modo da potere studiare con lo stesso circuito sia la carica (posizione A) che la scarica (posizione B).

Quindi si è fissata la forza elettromotrice erogata dal generatore a circa 12 V e posizionato il commutatore in A si è fatto partire il cronometro annotando il valore del potenziale ai capi del condensatore ad ogni intervallo di tempo prescelto.

Si è fatto un certo numero di misure fino a quando si è notato che la differenza di potenziale ai capi del condensatore C, cambiava troppo lentamente.

A questo punto si è escluso il generatore, spostando il commutatore nella posizione B in modo da fare iniziare il processo di scarica, si è avviato il cronometro e si sono annotati i tempi in cui la differenza di potenziale subiva una variazione prescelta DV fino a quando la differenza di potenziale ha assunto un valore molto prossimo allo zero.

A questo punto si è utilizzato il metodo del confronto per determinare il valore della capacità incognita.

Il metodo del confronto consente di misurare C_X facendolo scaricare attraverso la resistenza R e confrontando questo processo con quello di scarica di un condensatore noto C'. Nel processo di scarica di C_X tra i valori di tensione di V₁ e V₂ esistono le seguenti relazioni:

  e

Ne deriva:

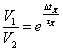
Dove Δt è l'intervallo di tempo in cui la tensione ai capi di C_X passa da V₁ a V₂.

Passando ai logaritmi:

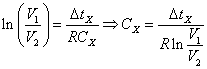
Ed analogamente per il condensatore C':

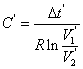
Si deve fare in modo che i valori di tensione tra cui si lascia scaricare i due condensatori siano gli stessi, ma purtroppo ciò è possibile entro gli errori di misura pertanto assumendo che:

Poiché C' è noto, misureremo gli intervalli temporali.

ANALISI DEI DATI :

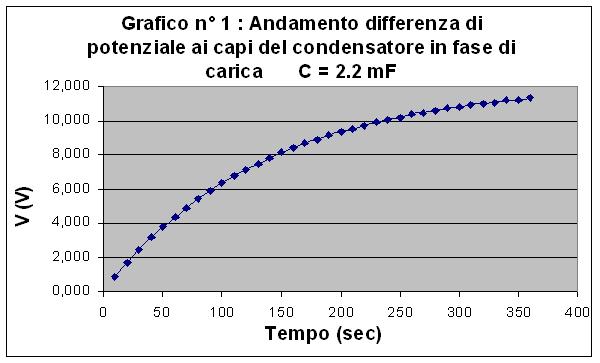
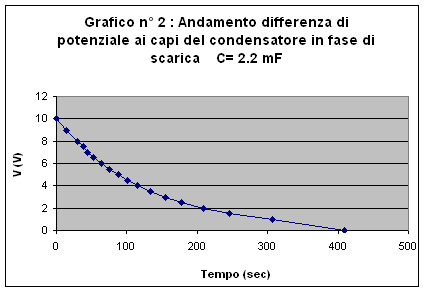
Dai dati sperimentali, riportati nelle tabelle seguenti si sono ottenuti gli andamenti di carica e scarica dei condensatori che come si può ben vedere mostrano un andamento esponenziale (crescente nella carica e decrescente nella scarica).

Come è stato già detto valgono per la carica e per la scarica le due relazioni:

le quali possono essere linearizzate passando ai logaritmi, ottenendo:

ponendo in questa:

x = t    a = ln e y = ln (e-V_C)   b = 1 / (RC)

si ha y = a - bx, quindi noto b = 1 / (RC) e noto R si può trovare la capacità incognita C.

Per la seconda relazione si ottiene:

Ponendo in questa:

y = ln V_C x = t a = ln V₀ b = -1 / (RC)

con queste sostituzioni otteniamo una relazione lineare y = a + bx.

Rettificheremo la seconda relazione per non introdurre una nuova fonte di errore dovuta a e. Per applicare il metodo dei minimi quadrati si è supposto trascurabile l'errore sui tempi.

Il fondo scala del voltmetro era di 20 V e quindi l'errore commesso nelle misurazioni delle differenze di potenziale è di 0.01 V. Questo valore è stato portato a 0.05 V per tenere conto del tempo di reazione nel leggere il valore del tempo t sul cronometro digitale al potenziale V_t.

Si è sfruttato questo errore per calcolare quello sulla pendenza ed infine propagando l'errore relativo su pendenza e sulla R (tolleranza) si è trovato l'errore su C.

Tale errore è risultato di circa il 5% infatti C = 2.4 mF 0.12 mF.

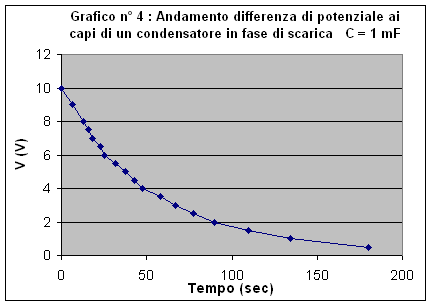
Passando invece al metodo del confronto, i limiti di V sono stati V_max= 10 V ed V_min= 0.5 V. Questo metodo ha fornito per C_x = 2.2 mF 0.2 mF. Quest'ultimo errore si è ottenuto dalla somma in quadratura degli errori relativi su t_x , t₀ e C₀.

Da una media pesata sui due valori risulta C_x 2.3 mF 0.1 mF.

Tabella n° 1 : Valori misurati durante la fase di carica con condensatore C = 2.2 mF

Tabella n° 2 : Valori misurati in fase di scarica con condensatore C= 2.2 mF

Retta dei minimi quadrati

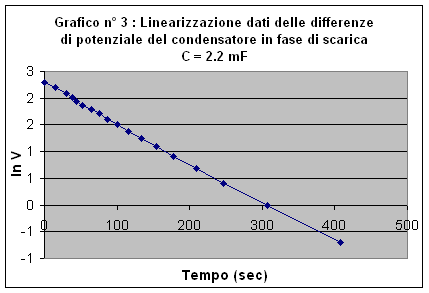
Pendenza    -0.00742 Errore su Pendenza 6.71e-05

Intercetta   2.27 Errore su Intercetta 0.01104

Coefficiente correlazione 0.9993

Resistenza     5600 W

Capacità 0.024 F

Tabella n° 3 : Valori misurati in fase di scarica con condensatore C=1 mF