OBIETTIVO :

Verifica della legge di riflessione e rifrazione per un raggio laser incidente su un blocco di plexiglas e misura dell'indice di rifrazione del materiale.

STRUMENTI :

N° 1 Blocco di Plexiglas;

N° 1 Sorgente laser;

N° 1 Calibro decimale;

N° 1 Goniometro con precisione di 0.5°;

N° 1 Schermo con carta millimetrata;

N° 1 Lastra di Plexiglas ad U recante una incisione centrale nel senso della lunghezza, che render 141c21b à possibile l'individuazione del raggio riflesso e l'angolo di riflessione.

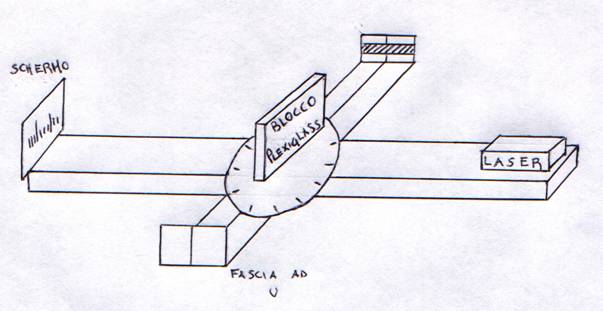
L'apparato è costituito da una barra di alluminio fissa alle cui estremità sono collocati la sorgente laser da una parte e lo schermo con carta millimetrata dall'altra. Al centro della barra di alluminio sono sovrapposti la lastra di plexiglas ad U, il goniometro di 360° ed una piattaforma su cui poggiare il blocco di plexiglas di cui dobbiamo calcolare l'indice di rifrazione. La lastra di plexiglas e la piattaforma possono ruotare al contrario del goniometro che è fisso. La piattaforma e la lastra di plexiglas ad U hanno movimenti indipendenti.

INTRODUZIONE TEORICA :

Diamo per assunto il concetto di raggio incidente, definiamo invece il punto di incidenza

come il punto in cui il raggio incidente colpisce la superficie di separazione dei mezzi interessati ed inoltre il piano di incidenza come il piano individuato dal raggio incidente e dalla normale nel punto di incidenza alla superficie.

La legge della riflessione stabilisce che:

Il raggio riflesso giace nel piano di incidenza;

L'angolo q_r tra il raggio riflesso e la normale alla superficie nel punto di incidenza è uguale all'angolo q_i tra il raggio incidente e la stessa normale.

La legge della rifrazione, invece stabilisce che:

Il raggio rifratto giace nel piano di incidenza;

Il rapporto tra i seni dell'angolo di incidenza e quello di rifrazione è costante e dipende dai mezzi interessati al fenomeno ottico. Il rapporto così individuato è chiamato indice di rifrazione relativo ai mezzi e può anche essere espresso come rapporto di due indici di rifrazione n₁ ed n₂ dove n₂ è l'indice di rifrazione del mezzo in cui il raggio si rifrange ed n₁ è l'indice di rifrazione del mezzo in cui il raggio incidente si propaga. Nel caso in questione l'indice di rifrazione dell'aria che poi è il nostro n₁ è 1.0029, noi considereremo uguale ad 1 tale indice allora la II parte della legge della rifrazione afferma che:

PROCEDIMENTO:

Prima di iniziare l'esperienza abbiamo determinato lo zero dell'apparato, ovvero abbiamo determinato ed evidenziato sullo schermo, il punto di incidenza del raggio in assenza del blocco di plexiglas che indurrebbe deviazioni nel percorso del raggio stesso. Abbiamo quindi sistemato sulla piattaforma il blocco di plexiglas in modo tale che il raggio laser, passando indeviato dal blocco, incidesse nello zero precedentemente individuato senza interferire con il nastro adesivo che è posto sul blocco stesso, si è verificata questa coincidenza di punti.

Siamo passati quindi alla verifica della legge della riflessione, abbiamo ruotato la piattaforma (e quindi il blocco) permettendo una variazione dell'angolo di incidenza del fascio luminoso. Si è ruotata più volte la piattaforma, con incrementi di 10° considerando positivi gli angoli ottenuti per rotazioni in senso orario e negativi quelli ottenuti per rotazioni anti-orarie.

Il raggio riflesso è stato individuato per mezzo della fascia di plexiglas ruotante ad U, in particolare con lo scopo di determinare l'esatto angolo di riflessione si è prestata particolare attenzione a fare coincidere il punto di incidenza con la linea centrale che è marcata sulla fascia di plexiglas nel senso della sua lunghezza.

Quindi con lo scopo di determinare l'angolo di riflessione q_r, abbiamo valutato l'angolo totale a tra il raggio incidente e quello riflesso, in formule:

ed allora

Variando l'angolo di incidenza, e misurando l'angolo a, con i metodi sopra esposti, abbiamo

raccolto i dati espressi in Tabella n° 1. Va osservato che i dati raccolti, sono però viziati da errori di eccentricità, dovuti al fatto che l'asse di rotazione della piattaforma e l'asse del goniometro potrebbero non coincidere.

Prima di procedere con la parte dell'esperienza riguardante la verifica della legge della rifrazione, abbiamo portato a termine due compiti preliminari.

Innanzitutto abbiamo determinato ancora una volta lo zero dell'apparato ed inoltre abbiamo verificato il parallelismo tra facce opposte del blocco di plexiglas. Riguardo al secondo compito abbiamo misurato in più punti e più volte lo spessore del blocco, i dati ricavati sono raccolti nella Tabella n° 2, è risultato evidente che le facce non sono perfettamente parallele.

L'angolo di rifrazione è stato misurato indirettamente sfruttando due metodi distinti. Posizionando il blocco sulla piattaforma e ruotando il blocco con incrementi successivi di 10° abbiamo misurato lo spostamento t, sulla carta millimetrata, del fascio incidente rispetto alla posizione assunta in condizioni di perpendicolarità tra raggio incidente e superficie del blocco, ed inoltre la distanza d, sulla prima faccia del blocco tra raggio incidente e raggio riflesso dalla seconda faccia, coperta con del nastro adesivo.

Approfondendo questi discorsi, il primo metodo si basa sul meccanismo delle riflessioni e rifrazioni sulle due facce del blocco: il raggio incidente entrando nel blocco si rifrange per poi riflettersi sulla seconda faccia rivestita di nastro adesivo. Il raggio riflesso torna indietro rifrangendosi sulla prima faccia e fuoriuscendo dal blocco sempre dalla prima faccia. Si è misurata la distanza tra il punto di ingresso ed il punto di uscita sulla prima faccia del blocco. Prendiamo in esame la figura seguente, che rappresenta il fenomeno appena descritto.

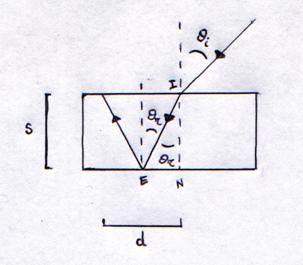
Abbiamo indicato la normale nel punto di incidenza sulla prima faccia ed il suo prolungamento. Il triangolo INE è rettangolo ed allora:

quindi

e trasformando

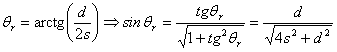
Con il secondo metodo invece focalizziamo l'attenzione sul raggio rifratto sulla seconda faccia del blocco che fuoriesce dal blocco rifrangendosi ancora una volta. In figura abbiamo espresso le rifrazioni descritte.

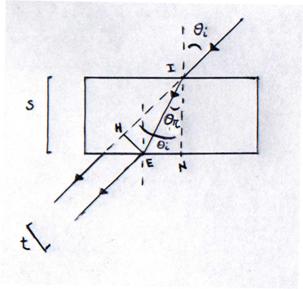
Allora sullo schermo otterremo un raggio uscente parallelo rispetto a quello incidente ed abbiamo misurato la distanza fra il punto di incidenza fra questo raggio e quello precedentemente segnato.

Consideriamo il triangolo IEH retto in h, allora:

e considerando il triangolo INE che

quindi

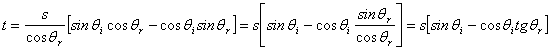
otterremo:

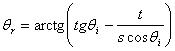
Le misure relative ai due metodi appena descritti sono raccolte nella Tabella n° 2.

ERRORI A PRIORE:

La stima dell'errore sulla singola misura dipende soltanto dalla sensibilità dello strumento. Assumiamo tale sensibilità come 0.5°, a tale precisione inoltre bisogna aggiungere 1° dovuto all'errore di parallasse (errore sistematico). L'errore sulla singola misura sarà allora dato dalla somma in quadratura dell'errore sistematico e di quello accidentale.

ANALISI DEI DATI:

Iniziamo dalla verifica della legge della riflessione, dalla teoria sappiamo che q_i q_r, se poniamo y = q_r ed y = q_r , otteniamo una relazione lineare del tipo y=x. Ci aspettiamo quindi che i nostri dati seguano un andamento lineare del tipo

dove m indica il coefficiente angolare della retta e q l'intercetta, con m 1 e q 0 entro gli errori.

Verificando questa dipendenza lineare avremo verificato la parte della legge della riflessione che riguarda l'uguaglianza degli angoli.

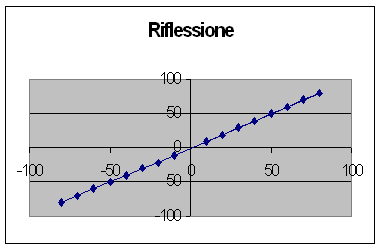
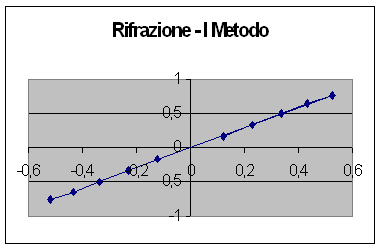
Una prima verifica della dipendenza lineare delle due misure si può ottenere dalla rappresentazione grafica dei punti, che abbiamo espresso nella Figura n° 1. Alla serie dei dati sperimentali è stato applicato il metodo dei minimi quadrati ricavando per m il valore di 1 0.0006 e per q il valore 0.44 0.14. Confrontando l'errore su m con lo stesso valore di m possiamo ritenere trascurabile l'errore e possiamo considerare m=1 e q=0.44 0.14, calcolando la dipendenza lineare otteniamo un coefficiente di correlazione di 0.98.

Passiamo ora alla verifica della legge della rifrazione. Utilizzando il primo metodo, la base delle relazioni è rappresentata da

dobbiamo verificare che

e con le sostituzioni y=sinq_r e x= sinq_i , m=1/n_plexiglas otteniamo ancora una volta una relazione del tipo y=mx+q. Applicando il metodo dei minimi quadrati ai dati rilevati sperimentalmente otteniamo m = 0.679 0.002 ed q = 0.007 0.001 con coefficiente di correlazione lineare 0.999 ottenendo fra l'altro un valore per n_plexiglas di 1.473.

Riguardo all'errore che commettiamo su n_plexiglas, questo è dato da:

otteniamo d_n

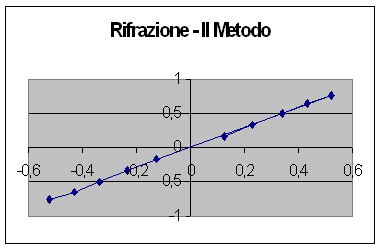
Verificando invece la legge della rifrazione con il secondo metodo, che parte dalla relazione:

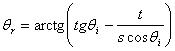
dobbiamo verificare che:

Adoperando il solito cambiamento di variabili dobbiamo verificare y = mx + q, questa volta otteniamo m = 0.678 0.003, q=0.0009 ed n_plexiglas di 1.474. Abbiamo ottenuto inoltre un coefficiente di correlazione lineare pari a 0.999. In merito all'errore che commettiamo su n_plexiglas abbiamo ottenuto d_n

Sia il primo che il secondo metodo hanno fornito un valore di n_plexiglas , diamo anche una stima dell'errore su questa stima. Partendo dalla relazione:

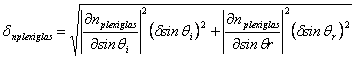
E considerando gli errori su sin q_i e su sin q_r possiamo calcolare d_nplexiglas per mezzo della formula di propagazione degli errori.

Se riteniamo trascurabile l'errore su sinq_i , possiamo giungere ad una stima di dn_plexiglas comnsiderando dsinq_r sia dal primo metodo che dal secondo.

Se si parte dall'errore dsinq_r derivante dal primo metodo e ricordando che, sempre dal primo metodo, abbiamo:

Applicando a questa definizione di sinq_r la formula di propagazione dell'errore si ha:

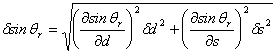
Effettuando le sostituzioni otteniamo d_nplexiglas=0.004. Se applichiamo la stessa metodologia sin qui vista al secondo metodo ove alla espressione di sinq_r si vada a sostituire l'espressione base per il metodo:

(andremo banalmente a considerare sin(arctg(tgq_r))) e propagando l'errore otterremo d_nplexiglas

Abbiamo a disposizione due valori di n_plexiglas con relativi errori derivati da metodi distinti, calcoliamo allora la media pesata fra questi due valori ed il relativo errore:

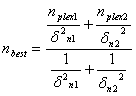
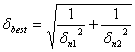
E sostituendo otteniamo n_best = 1.478 ed d_best

Tabella n° 1 : Misura dell'angolo di riflessione

Tabella n° 2 : Misura spessore del blocco di plexiglas con l'ausilio del calibro cursore

Valore medio spessore blocco di plexiglas 4.46 cm

Tabella n° 3 : Misure relative ai due metodi per la verifica della legge della rifrazione

Coefficiente correl. lineare retta I Metodo 0.999 Err. Y1 0.003

Intercetta retta I Metodo    0.0007 Err. 1 0.001

Coefficiente Angolare retta I Metodo 0.679 Err. Coeff. Angol. I Metodo 0.002

Indice rifrazione I Metodo   1.473 Err. Indice rifraz. I Metodo 0.004

Coefficiente correl. lineare retta II Metodo 0.999 Err. Y2 0.005

Intercetta retta II Metodo   0.0009 Err. 2 0.001

Coefficiente Angolare retta II Metodo 0.678 Err. Coeff. Angol. II Metodo 0.003

Indice rifrazione II Metodo  1.473 Err. Ind. rifraz. II Metodo 0.004