Laboratorio di Fisica - Legge dei punti coniugati

Principi teorici:

la legge dei punti coniugati è un'applicazione dell'ottica geometrica. L'ottica geometrica studia il comportamento di fenomi semplici interpretati mediante leggi di carattere geometrico. Tali leggi sono:

propagazione rettilinea della luce;

indipendenza dei raggi luminosi;

riflessione della luce su una superficie speculare;

rifrazione della luce sulla superficie di separazione di due mezzi trasparenti.

Materiale usato

Banco ottico tarato, di circa 1,20m con scala graduata (sensibilità 1mm) su cui poggiavano tre supporti: lo schermo, su cui si raccolgono le immagini;una lente convergente, più grossa al centro che agli orli, capace di convergere i raggi luminosi; proiettore, costituito da una lampada a incandescenza con lente condensatrice.

Procedimento:

abbiamo cominciato la nostra esperienza di laboratorio fissando la lente e l'oggetto in modo che fosse messo a fuoco e facendo successivamente 10 misure di p e delle corrispondenti q stimando anche gli errori e fissando inizialmente i valori p_max e p_min.

I valori di p sono stati calcolati misurando semplicemente la distanza tra la lente convergente e l'oggetto, spostando la p di un'intervallo pari a 2.4 cm, calcolato facendo p_max-p_min/ 10.

L'errore di p viene stimato determinando dove è il centro della lente a rigore p è la distanza tra centro della lente ed oggetto.  

Per le rispettive q essendo la definizione di immagine a fuoco assai oggettiva, dopo aver cercato in prima approssimazione la giusta distanza di messa a fuoco,abbiamo preso in considerazione due q :

q_min e q_max.

La q_min è stata calcolata avvicinando lo schermo verso la lente finchè l'immagine sembrava cominciare ad andare fuori fuoco.

La q_max ,invece, è stata calcolata spostando lo schermo nella direzione opposta fino al punto in cui l'immagine cominciava ad andare nuovamente fuori fuoco.

La migliore stima di ciascuna q è stata quindi ottenuta attraverso la semisomma di queste ultime:

(q_min + q_max) / 2.

Mentre i rispettivi errori Δq ,calcolando la loro semidifferenza:

(q_min - q_max) / 2.

Abbiamo ottenuto i seguenti valori:

Ottenuti i valori di p e q ,abbiamo in seguito calcolato i loro reciproci con una semplice divisione:

1/p e 1/q

Il seguente grafico riporta i valori di 1/p in funzione di 1/q :

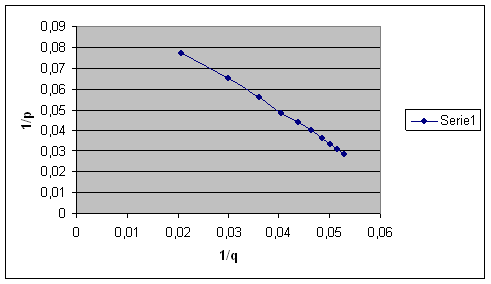
A questo punto, consideriamo 1/p la variabile indipendente Y e 1/q quella dipendente X,

attraverso il metodo dei minimi quadrati  Y=AX+B, calcoliamo 1/f.

1/f ,infatti, non è altro che l'intercetta della nostra retta che si adatta alla nostra curva nel grafico 1/p in funzione di 1/q.

Servendoci del programma EXCEL abbiamo ricavato la PENDENZA (A) e l'INTERCETTA (B)

della nostra retta.

B = 1/f =0

A  =

Fatto ciò ora possediamo tutti gli elementi per poter determinare la nostra distanza focale f.

Il valore di f lo si ottiene semplicemente calcolando il reciproco di 1/f.

F= 1/B=