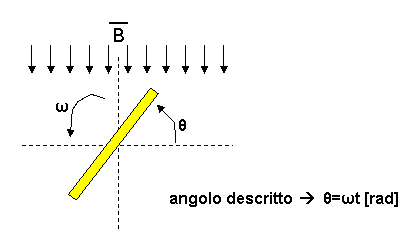
Quando è uguale a 90°, la velocità istantanea v dei conduttori è perpendicolare alle linee di induzione e la tensione generata assume il valore massimo (E_max).

Negli altri istanti la tensione è data da:

e = E_maxsen = E_maxsen t  

E_max  E

θ

T periodo, tempo necessario affinchè la bobina compia una rotazione

,completa ( per descriverr l'angolo

T=2π/

F= 1/T= ω/ 2πf

Fase di una sinusoide

Se il passaggio per lo zero avviene nell'istante t=0 :

e = E_maxsen = E_maxsen t

Se il passaggio per lo zero avviene nell'istante t₁ , l'angolo corrispondente al tempo t₁ è denominato fase φ.

Φ=ωt₁ = 2πt₁ /T [rad]

L'espressione analitica della sinusoide diventa

e = E_maxsen( t+ φ)

e = E_maxsen(2πft+φ)    FASE ISTANTANEA t+ φ

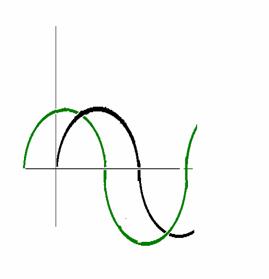 La funzione in verde è sfasata rispetto a

quella in verde

Per descrivere segnali periodici di forma diversa da quella sinusoidale si considera solamente una parte di essi, in modo che non abbiano valori nulli: si studiano quindi in modo isolato.

E' possibile studiare ed ottenere la funzione matematica di un segnale periodico di forma d'onda regolare, considerando impulsi con lo stesso andamento.

IMPULSO DI DIRAC

L'impulso di Dirac ( o impulso ideale o impulso unitario di Dirac) è un impulso applicato all'origine dei tempi, con ampiezza infinita e durata nulla (t=0).

Per arrivare all'impulso di Dirac, si considera un impulso rettangolare di area unitaria (costante).

T è la durata di tale impulso.

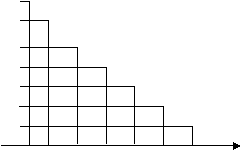
Si suppone di ridurre gradualmente la durata dell'impulso rettangolare. Essendo l'area unitaria, si ottengono impulsi sempre più stretti ed alti:

A

0 t

L'impulso tende ad un'altezza infinita, sempre con area unitaria. Questa è una funzione limite f(t), detta, appunto, impulso di Dirac. Si indica con (t):

δ(t)= lim f(t)

^t

Al limite per t 0, l'impulso tende ad un'altezza infinita, sempre con area unitaria.

0 per t

δ(t[m1] )

∞ per t=0

A

0 t

Se si considera un treno di impulsi e non un impulso isolato, si fa riferimento alla somma dei singoli impulsi

f(t)= Σδ(t-nt₀)

ⁿ

dove t₀ indica il ritardo fra un impulso e il successivo.

IMPULSO RETTANGOLARE

Un impulso rettangolare è un segnale di ampiezza A costante e durata T .

Assume valori nulli in tutti gli altri istanti di tempo.

.f(t)

A T=1/f

-T/2 T/2 t

T t= ±T/2

f(t)=Aret( t/T)

t/T= ±1/2 Indica la variazione del segnale nel tempo rispetto all'asse y,   

riferita alla durata T dell'impulso.

A se -T/2≤ |T|≤ +T/2

Ret(t)

0 se T<-T/2 ; T>T/2

Un impulso traslato rispetto all'origine e centrato in un istante t₀ ha come equazione :

f(t) = Aret [(t-t₀)/T] con (t-t₀)/T=±1/2

Se si considera un segnale rettangolare periodico ( e no isolato), si può fare riferimento ad una somma di impulsi.

f(t)= ΣAret [(t-nt₀)/ ]

ⁿ

dove n è un numero intero pari e è un valore minore di T.

IMPULSO TRIANGOLARE

Un impulso triangolare è un segnale di durata T che assume diversi valori di ampiezza A e valori nulli in tutti gli altri istanti di tempo.

A

-T/2 T/2 t

Si può esprimere attraverso formale matematicamente:

0 se T<-T/2 ; T>T/2

f(t)=tr(t)=

A - A(|T|/T/2) se -T/2≤ |t|≤ +T/2

1/2≤ t/T ≤1/2 f(t)=A - A·tr(t/T)

Se si considera l'impulso traslato nel tempo all'istante t₀, si ha:

f(t)=A[1-tr(t-t₀)/T]-t-t₀/T

Un segnale triangolare periodico può essere considerato come somma di singoli impulsi triangolari:

f(t)= ΣA[1-tr(t-nT)] T corrisponde a to n è un numero intero

ⁿ

IMPULSO DI NYQUIST

Un impulso di Nyquist (o impulso ad oscillazione smorzata) è un segnale di durata T, centrato all'origine dei tempi (dove ha la massima ampiezza A), con andamento oscillatorio armonico spezzato.

f(t)

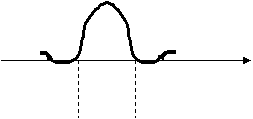
-T T t

T

La sua espressione è data da:

f(t)= [Asen(πt/T)]/(πt/T)=Asenxt/xt x=π/T

Questo segnale è considerato come una funzione temporale in un intervallo compreso tra -∞ e +∞, ossia come somma dei singoli impulsi.

_∞

f(t)=ΣAsenxt/xt

^t=-∞

FATTORE DI FORMA: parametro riguardante i segnali bipolari

F_f=V_eff/V_m    Si definisce in un semiperiodo T/2

FATTORE DI CRESTA:

F_p=V_m/V_eff    Si definisce in un semiperiodo T/2

---