|
|
| |
 leggi del pendolo, relazione tra
lunghezza del pendolo e periodo di oscillazione.
leggi del pendolo, relazione tra
lunghezza del pendolo e periodo di oscillazione.
Prima parte
Che cos'è un pendolo?
![]()



![]()
![]()
![]()
![]()
![]()

![]() Il pendolo è un'asta rigida (che non si allunga)
come un filo di peso trascurabile alla cui estremità si trova un corpo con una
massa non trascurabile. L'asta rigida ad un'estremità è vincolata, mentre all'altra
è collegata all'oggetto.
Il pendolo è un'asta rigida (che non si allunga)
come un filo di peso trascurabile alla cui estremità si trova un corpo con una
massa non trascurabile. L'asta rigida ad un'estremità è vincolata, mentre all'altra
è collegata all'oggetto.
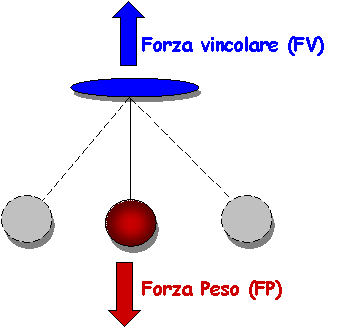
Quando il pendolo è in posizione verticale si dice che 111g61b si trova in posizione di equilibrio. Questa posizione viene raggiunta quando le forze che agiscono sul pendolo si equivalgono e perciò si annullano a vicenda.
![]()



![]()
![]()

![]()
La forza vincolare agisce solo nel senso dell'asta. La forza risultante è pari alla somma delle due forze e ciò tende a farle riavvicinare alla posizione di partenza e quindi a quella di equilibrio. Il pendolo però non si fermerà in questa posizione visto che ha accumulato una certa velocità e per inerzia continuerà a muoversi cercando di mantenere sempre la stessa velocità. Se oltre a queste forze non ne esistesse un'altra il pendolo continuerebbe ad oscillare per sempre. Ma esiste anche un'altra forza, che è la forza di attrito, come quella dell'aria e del punto in cui il filo si piega, che tende a far rallentare il pendolo fino a farlo fermare.




![]()
![]()
![]()
![]()
![]()
Gli esperimenti di Galileo Galilei
Galileo Galilei studiò il moto del pendolo nel Duomo di Pisa, osservando le oscillazioni compiute da una lampada appesa al soffitto. Si accorse che, mentre l'ampiezza delle oscillazioni e la velocità del pendolo variavano, la durata di una oscillazione rimaneva sempre uguale. Questo perché piano piano, per l'attrito, il pendolo perde velocità e proporzionalmente a questa diminuzione della velocità diminuisce anche l'ampiezza delle oscillazioni, per cui il tempo impiegato è sempre uguale.
Galileo galilei compiuti i suoi studi sul pendolo trovò le tre leggi del pendolo, che sono:
il tempo di oscillazione, cioè il periodo (T) non dipende dall'ampiezza delle oscillazioni per piccole oscillazioni;
il periodo non dipende dalla massa del pendolo;
il periodo dipende alla lunghezza del pendolo.
Seconda parte
Procedimento:
![]() fare cinque pendoli con lunghezze diverse.
fare cinque pendoli con lunghezze diverse.
![]() Misurare il tempo impiegato per compiere dieci
oscillazioni e poi (dividendo per dieci) trovare il tempo impiegato per
compiere una oscillazione
Misurare il tempo impiegato per compiere dieci
oscillazioni e poi (dividendo per dieci) trovare il tempo impiegato per
compiere una oscillazione
![]() Trovare la relazione che c'è fra la lunghezza del
pendolo e il periodo di oscillazione.
Trovare la relazione che c'è fra la lunghezza del
pendolo e il periodo di oscillazione.
![]() Determinare di quale tipo di proporzionalità di
tratta.
Determinare di quale tipo di proporzionalità di
tratta.
Proporzionalità diretta = y = k x (y/x =k)
Proporzionalità quadratica = y = k x² (y/x²= k)
Proporzionalità inversa = y = k/ x
Proporzionalità inversa quadratica = y = k/x²
 Lunghezza = misura della
lunghezza del pendolo dal vincolo al centro del peso.
Lunghezza = misura della
lunghezza del pendolo dal vincolo al centro del peso.
Esperimento
L 100 cm T 19.92 s - 19.54 s - 20.33 s
T (medio) = 19.93 s 1T 1.99 s
L 81 cm T 18.02 s - 17.76 s - 18.07 s
T (medio) = 17.95s 1T 1.8 s
L cm T³= 16.93 s - 16.39 s - 16.6 s
T³ (medio) = 16.64 a 1T³=1.66 s
L 49 cm T 14.29 s - 14.02 s - 13.92 s
T (medio) = 14.08 s 1T 1.41 s
L = 37 cm T 12.28 s - 12.11 s - 12.12 s
T (medio) = 12.17 s 1T 1.22 s
|
LUNGHEZZA (cm) |
PERIODO (s) |
L/T (cm/s) |
L/T² (cm/s²) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Come si vede dal grafico e dalla tabella non si può trattare di proporzionalità inverse ne proporzionalità inverse quadratica, visto che all'aumentare della lunghezza aumenta anche il periodo. Per cui può essere so proporzionalità diretta o quadratica. Ma visto che nel grafico non si ha una linea retta passane per l'origine ed eseguendo il calcolo lunghezza/periodo non si raggiunge una costante, si può dire il rapporto che c'è tra la lunghezza del pendolo e il periodo di oscillazione gode di proporzionalità quadratica.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026