FISICA
Dopo aver descritto i modelli cosmologici, eliocentrici e geocentrici e
le ragioni del loro affermarsi, enuncia le 3 leggi del moto dei pianeti di
Keplero, la legge di gravitazione universale di Newton e spiega perché il peso
di un corpo varia, mentre la massa è una caratteristica universale.
Nel corso della storia, varie sono state le ipotesi sulla collocazione
del Sole e della Terra nell'Universo. Il primo ad elaborare una ipotesi
geocentrica fu Eudosso di Cnido (408-355 a.C.), che elaborò una teoria che assumeva la Terra immobile al centro
dell'universo. Tutti i pianeti, compreso il Sole, si muovevano intorno alla
Terra seguendo orbite circolari, tutte concentriche alla Terra. Ciascun pianeta
era sostenuto da un certo numero di sfere concentriche, "annidate" l'una
nell'altra, motivo per il quale, molti
secoli dopo, il sistema divenne noto come sistema delle sfere omocentriche. Aristotele nel III sec. a.C. portò avanti la
teoria di Eudosso di Cnido, sostenendo che il mondo celeste fosse costituito di
una mateia incorruttibile, l'etere o quintessenza, contrapposto al mondo
sublunare costituito dai 4 elementi (terra, acqua, aria e fuoco) che gli davano
la natura corruttibile; un altro importante elemento del pensiero aristotelico,
fu il collegamento tra la fisica e la metafisica, visto dal filosofo nel
"Motore immobile" che era quell'ente che muoveva le sfere celesti e il cosmo,
senza però essere mosso da nulla di esterno a sé stesso. Tale concezione
condizionò il pensiero occidentale e la scienza fino ai tempi di Galileo. Nel
II sec. a.C, l'astronomo Tolomeo propose una teoria che, assumendo la Terra immobile al centro
dell'universo, descriveva in temini geometrici e matematici i moti e le
posizioni dei pianeti, del Sole e della Luna su uno sfondo di stelle fisse. Il
sistema tolemaico prevede che i corpi celesti, quali la Luna, Mercurio, Venere, il
Sole, Marte, Giove e Saturno, ruotino intorno alla Terra percorrendo orbite
perfettamente circolari, dette deferenti. Per spiegare le
irregolarità osservate nei moti dei pianeti e i cambiamenti di dimensione e di
luminosità dei corpi celesti, Tolomeo sostenne che solo il Sole percorresse il
proprio deferente con moto uniforme, e che la Luna, e in generale gli altri pianeti, si
muovessero su piccoli cerchi, detti epicicli,
i cui centri si muovevano a loro volta sui relativi deferenti. Il sistema
tolemaico elaborato con la complessa teoria degli epicicli poteva giustificare la maggior parte delle osservazioni
astronomiche dell'epoca, ma faceva ricorso a procedimenti geometrici estranei
ai postulati della matematica tradizionale. Contrapposta alla teoria
geocentrica, un altro astronomo, Aristarco di Samo, tra il IV e il III sec.
a.C. elaborò una ipotesi secondo cui le stelle fisse e il Sole erano immobili; la Terra si muoveva intorno al
Sole lungo l'eclittica, ruotando contemporaneamente su se stessa. Aristarco
spiegò inoltre l'alternarsi delle stagioni con l'inclinazione dell'asse
terrestre, la quale non è perfettamente perpendicolare al piano dell'orbita
compiuta attorno al Sole. E' noto, tuttavia, che egli fu condannato per empietà
e come corruttore della gioventù per aver insegnato la teoria eliocentrica.
La sua principale intuizione, l'eliocentrismo, oggetto di numerose
critiche, cadde ben presto nel dimenticatoio, fino all'avvento di Copernico. Questo
grande astronomo e matematico polacco, nel XVII secolo, dimostrò che i pianeti
ruotavano intorno al Sole descrivendo orbite circolari e che il resto del cielo
con le stelle fisse, rimaneva immobile intorno al sistema solare. Negli stessi
decenni, Galileo Galilei, grande scienziato toscano, attraverso l'uso del cannocchiale
dimostrò l'omogeneità tra il mondo celeste e quello sublunare, dimostrando
l'inesattezza del postulato Aristotelico. Alcuni anni più tardi, l'astronomo
tedesco Keplero, introdusse, provandolo matematicamente, che i pianeti
descrivevano intorno al Sole orbite ellittiche, e dimostrò ciò con 3 leggi:
I. I pianeti
descrivono orbite ellittiche intorno al Sole, che è posto in uno dei due fuochi
dell'ellisse.
II. Il raggio
vettore, che congiunge il centro del pianeta col centro del Sole, spazza aree
uguali, in tempi uguali.
III. I
quadrati dei periodi di rivoluzione dei pianeti sono proporzionali ai cubi dei
semiassi maggiori delle loro orbite ellittiche:
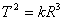
dove R è il semiasse maggiore
dell'orbita di un pianeta, k è una
costante di proporzionalità ricavabile dalla legge si gravitazione universale, T è il periodo di rivoluzione di quel
pianeta. Dopo aver dimostrato la forma ellittica dell'orbita, bisognava
dimostrare la natura della forza che fa mantenere ai pianeti un'orbita
ellittica costante, ciò avvenne grazie all'enunciazione della Legge di gravitazione universale di Newton
. Questo grazie ad osservazioni dirette dell'universo mediante un telescopio,
intuì che la forza di attrazione tra la Terra e la Luna è direttamente proporzionale al quadrato
della loro distanza, estendendo ciò a tutti i corpi dell'universo, si ottiene
che:
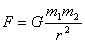
dove 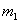 ed
ed 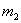 sono le masse di due
corpi qualsiasi, r è la distanza a
cui sono posti e G è una costante di
gravitazione universale il cui valore è
sono le masse di due
corpi qualsiasi, r è la distanza a
cui sono posti e G è una costante di
gravitazione universale il cui valore è 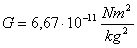 .
.
Ogni corpo
nell'universo è caratterizzato da una massa specifica e costante, il suo peso
invece è direttamente collegato all'intensità della forza peso cui il corpo è
sottoposto, proprio perché a seconda della massa dalla quale il corpo è
attratto, dalla legge di gravitazione universale si ricava che ogni corpo
celeste ha una propria accelerazione di gravità (g), che moltiplicata per la massa determina il peso del corpo ( P = mg ). Ad esempio, un sasso di
massa 1 kg,
sulla Terra che ha una g pari a 9,8 m/s² , il suo peso sarà P = 9,8 m/s²
1 kg = 9,8 N; lo stesso sasso di massa 1kg, su
Marte che ha g uguale a 3,76 m/s², il suo peso sarà pari a 3,76
N.
![]()
![]()
![]() ed
ed ![]() sono le masse di due
corpi qualsiasi, r è la distanza a
cui sono posti e G è una costante di
gravitazione universale il cui valore è
sono le masse di due
corpi qualsiasi, r è la distanza a
cui sono posti e G è una costante di
gravitazione universale il cui valore è ![]() .
.