|
|
| |
Vettore
Ente geometrico atto a descrivere grandezze fisiche e matematiche caratterizzate da un valore numerico o modulo, da una direzione e da un verso. (Sono vettori la velocità di un corpo, la sua accelerazione, tutte le forze, i momenti angolari, il gradiente di una funzione.)
Grandezza rappresentata graficamente con una freccia, il vettore è caratterizzato da modulo (intensità), direzione (retta su cui agisce) e verso (senso di percorrenza della retta stessa), ed esprime 727g62h una grande quantità di grandezze fisiche, come la velocità, l'accelerazione, le forze ecc. In termini matematicamente corretti, il vettore va definito come un ente geometrico che possiede una data legge di trasformazione rispetto a un cambiamento di sistema di riferimento. Si considerino all'uopo tutti i sistemi di coordinate ortogonali cartesiane nello spazio euclideo a tre dimensioni. Siano A, B due tali sistemi e xA, yA, zA xB yB, zB rispettivamente le coordinate cartesiane in A e in B. È noto che tra queste due terne di coordinate sussiste una legge di trasformazione del tipo:
xA=a+p11 xB+p12 yB+p13 zB
yA=b+p21 xB+p22 yB+p23 zB
zA=c+p31xB+p32 yB+p33 zB
dove a, b, c
sono le coordinate dell'origine di B nel sistema A e le pmn sono gli elementi di una matrice
ortogonale P. Un vettore v è definito
quando siano dati per ciascun sistema di riferimento A tre numeri reali ![]() (ma è facile generalizzare il concetto a un
anello qualsiasi), detti componenti del vettore, soddisfacenti alla legge di
trasformazione:
(ma è facile generalizzare il concetto a un
anello qualsiasi), detti componenti del vettore, soddisfacenti alla legge di
trasformazione:
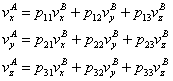
Dalle relazioni precedenti si può facilmente
verificare che l'inversione spaziale, definita dalla trasformazione x' = - x, y' = -y, z' = -z, induce un cambiamento di segno delle
componenti di v, cioè ![]() ;
un vettore che si comporta in questo modo rispetto all'inversione spaziale
viene detto vettore polare per
distinguerlo da un altro tipo di vettore, detto pseudovettore o vettore
assiale a che si trasforma come v rispetto alle rotazioni proprie (cioè
senza inversione), ma che è invariante rispetto all'inversione spaziale, cioè a' = a.
Esempi di vettori assiali sono il prodotto di uno pseudoscalare per un vettore
polare o il prodotto vettoriale di due vettori polari. L'importanza della
nozione di vettore risiede nel fatto che essa permette di esprimere proprietà
geometriche dello spazio euclideo e leggi fisiche in maniera indipendente da
ogni sistema di riferimento. Il concetto di vettore può essere semplicemente
generalizzato a spazi euclidei o riemanniani di dimensioni qualsiasi. Siano dati nello spazio euclideo un campo vettoriale v(P) e un campo scalare, s(P). Su di essi possono agire le
seguenti operazioni differenziali aventi un significato intrinseco:
;
un vettore che si comporta in questo modo rispetto all'inversione spaziale
viene detto vettore polare per
distinguerlo da un altro tipo di vettore, detto pseudovettore o vettore
assiale a che si trasforma come v rispetto alle rotazioni proprie (cioè
senza inversione), ma che è invariante rispetto all'inversione spaziale, cioè a' = a.
Esempi di vettori assiali sono il prodotto di uno pseudoscalare per un vettore
polare o il prodotto vettoriale di due vettori polari. L'importanza della
nozione di vettore risiede nel fatto che essa permette di esprimere proprietà
geometriche dello spazio euclideo e leggi fisiche in maniera indipendente da
ogni sistema di riferimento. Il concetto di vettore può essere semplicemente
generalizzato a spazi euclidei o riemanniani di dimensioni qualsiasi. Siano dati nello spazio euclideo un campo vettoriale v(P) e un campo scalare, s(P). Su di essi possono agire le
seguenti operazioni differenziali aventi un significato intrinseco:
Gradiente. Il campo vettoriale grad (s) ha per componenti
![]()
Il gradiente di una costante è nullo. Dati due punti P, P + dP molto vicini, il prodotto scalare (grad s, dP) dà l'incremento ds di s da P a P + dP.
b) Divergenza. La funzione
![]()
è un campo scalare.
c) Rotore. Esso è un campo pseudovettoriale definito formalmente dalla relazione rot v = grad
Identità differenziali. Esse sono:
rot (grad (s)) = 0, div (rot v) = 0.
Inoltre l'operatore di Laplace è definito da div (grad s) = s e dà di nuovo un campo scalare. Chiaramente si ha
![]()
Lo stesso operatore si può applicare a un campo vettoriale ottenendo un campo vettoriale. Sussiste l'identità:
rot (rot v) = grad (div v)
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025