|
|
| |
QUANTITÀ DI MOTO
La quantità di moto è una grandezza dinamica per un punto materiale; se il corpo è composto da più punti materiali, si introducono i sistemi.

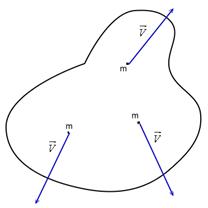
Per il secondo principio della dinamica, quando si
applica una forza a una massa ![]() , questa accelera modificando la su 545h79f a velocità iniziale e
quindi anche la sua quantità di moto.
, questa accelera modificando la su 545h79f a velocità iniziale e
quindi anche la sua quantità di moto.
![]()
A questo punto si può descrivere la quantità di moto come il prodotto di una forza per un intervallo di tempo, che prende anche il nome di IMPULSO.
|
Non tutte le forze che interagiscono con un corpo sono tali da modificare la sua quntità di moto. Infatti per il terzo principio della dinamica tutte le forze interne a un sistema si elidono tra loro; quindi le uniche in grado di modificare la quantità di moto di un sistema sono le forze esterne a questo. A questo punto si può definire che i sistemi isolati mantengono costante la loro quantità di moto. L'unico inconveniente è che che l'unico vero sistema isolato è l'universo, ma anche nei casi delle forze impulsive o di forze esterne relativamente molto piccole altri sistemi possono esser considerati isolati. |
|
La campana del grafico indica una forza impulsiva la cui intensità elevata e crescente, applicata in un intervallo di tempo brevissimo può cambiare notevolmente la quantità di moto di un corpo.
|
MODELLO STANDARD
interazione gravitazionale trascurabile
Nel modello standard c'è una netta divisione tra FERMIONI e BOSONI.
Analizzando i fermioni, possiamo dire che questi sono ulteriormente divisi a loro volta in QUANK e LEPTONI.
|
|
Up |
|
charm |
|
top |
|
( |
|
down |
strange |
bottom |
|
Quark (FED, FF)
Leptoni (FED)
|
|
Neutrino elettronico |
|
Neutrino muonico |
|
Neutrino tauonico |
|
elettrone |
muone |
tauone |
In natura vengono usate solo tre di tutte queste particelle, mentre delle altre non si sa nulla perché altamente instabili.
Tra gli intermediari delle particelle, i bosoni, se ne possono notare quattro differenti.
|
|
|
Diagramma di Faymman |
g (fotone)
w w
Z
CAMPO GRAVITAZIONALE
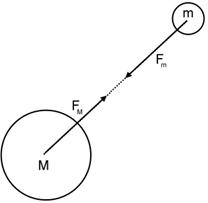 Secondo il terzo principio
della dinamica,
Secondo il terzo principio
della dinamica, ![]() .
.
Come afferma la legge di Newton, o più comunemente detta legge di gravitazione universale, il valore scalare della forza attrattiva che è esercitata dalle due masse è
![]()
Dove ![]() è uguale a
è uguale a ![]() .
.
Considerando come si calcola la forza peso seguendo
il secondo principio della dinamica, si può dimostrare che ![]() è solo
un'approssimazione della legge di Newton a altezza nulla.
è solo
un'approssimazione della legge di Newton a altezza nulla.
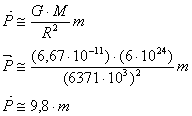
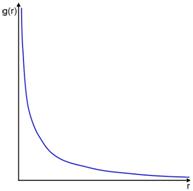 Quindi si può definire
l'accelerazione gravitazionale
Quindi si può definire
l'accelerazione gravitazionale ![]() come il campo
gravitazionale in funzione della distanza.
come il campo
gravitazionale in funzione della distanza.
Il campo gravitazionale ha raggio d'azione infinito, indipendentemente dai corpi (al contrario della forza gravitazionale che è dipendente da un secondo corpo).
A questo punto si può affermare che il campo gravitazionale è l'intermediario tra due corpi e inoltre possiede sia quantità di moto che energia.
![]() è conservativa.
è conservativa.
|
|
|
|
|
|
VELOCITÁ ORBITALE
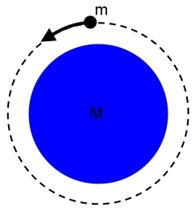

|
I Keplero |
I pianeti descrivono orbite ellittiche delle quali il Sole occupa uno dei due fuochi. |
|
II Keplero |
Il raggio vettore di un pianeta spazia aree uguali in tempi uguali. |
|
III Keplero |
Il quadrato dia tempi di rivoluzione è proporzionale al cubo del semiasse maggiore. |
VELOCITÁ ORBITALE
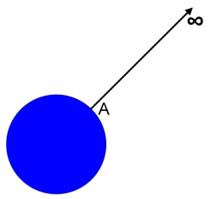
la velocità di fuga è la velocità che deve possedere un corpo per scappare fino all'infinito.

La
velocità massima alla quale un corpo può arrivare è quella della luce (![]() )
)
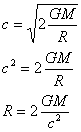
Raggio di Schwarzchild è il raggio che deve possedere un corpo in modo tale che neppure la luce sia in grado sia in grado di fuggire da questo; in pratica è il raggio che un corpo deve avere per diventare un buco nero.
MOMENTO DI UNA FORZA
Si è sempre definito che quando su un corpo ![]() questo rimane in
quiete, ma questa condizione non è sufficiente perché determina solamente che
l'oggetto non può traslare ma potrebbe sempre ruotare.
questo rimane in
quiete, ma questa condizione non è sufficiente perché determina solamente che
l'oggetto non può traslare ma potrebbe sempre ruotare.
Quindi un corpo per stare in quiete non deve né traslare né ruotare.
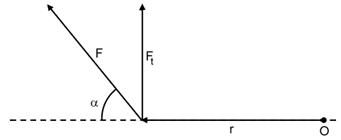 In una rotazione, maggiore è
la forza applicata e più efficace sarà il risultato;però se la retta d'azione è
passante per il polo, la rotazione sarà nulla.
In una rotazione, maggiore è
la forza applicata e più efficace sarà il risultato;però se la retta d'azione è
passante per il polo, la rotazione sarà nulla.
![]()
Influente sull'efficacia di una rotazione è anche la distanza tra il polo e il punto di applicazione di una forza.
![]()
Quindi si può definire il momento di una forza come il prodotto vettore tra il vettore posizione e una forza.
Poiché il momento è determinato da una sola forza e poiché su un corpo possono esser applicate più forze, un corpo si trova in una situazione di quiete solo se sia la sommatoria delle forze che dei momenti è nulla.
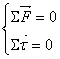
MOMENTO ANGOLARE
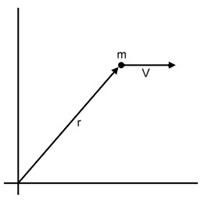 Il momento angolare è il
prodotto vettore tra il vettore posizione e la quantità di moto.
Il momento angolare è il
prodotto vettore tra il vettore posizione e la quantità di moto.
![]()
Se
la sommatoria delle forze applicate a un corpo non è nulla (![]() ), questa può esser considerata come la differenza della
quantità di moto in un arco di tempo.
), questa può esser considerata come la differenza della
quantità di moto in un arco di tempo.
![]()
Parallelamente,
se la sommatoria dei momenti delle forze non è nulla (![]() ),questa può esser considerata come la differenza del momento
angolare in un arco di tempo.
),questa può esser considerata come la differenza del momento
angolare in un arco di tempo.
![]()
![]() è il momento angolare
che possiede il corpo in un seguente istante di tempo tendente a 0, che è
quindi possibile scrivere come
è il momento angolare
che possiede il corpo in un seguente istante di tempo tendente a 0, che è
quindi possibile scrivere come ![]()
![]()
Essendo
![]() una quantità
infinitamente piccola (infinitesimo di ordine superiore), può esser trascurata.
una quantità
infinitamente piccola (infinitesimo di ordine superiore), può esser trascurata.
![]()
L'angolo
compreso tra il vettore velocità e il vettore quantità di moto è nullo, quindi
il loro prodotto vettore (![]() ) è a sua volta nullo.
) è a sua volta nullo.
![]()
Riassumendo, quando un corpo non si trova in una situazione di quiete
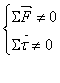
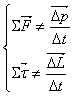
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025