CORSO DI BIOTECNOLOGIE - la capacità elettrica di un condensatore

  5 resistenze elettriche diverse;

  basetta per il cablaggio dei circuiti elettronici;

  pila dal valore nominale di 9 V;

  3 cavetti di collegamento con morsetti a coccodrillo alle estremità;

  carta millimetrata per la costruzione dei grafici;

  cavi con spinotti per il multimetro;

STRUMENTI DI MISURA

FASI DI ESECUZIONE DELL'ESPERIENZA

calcolo del valore nominale delle resistenze attraverso la decodificazione dei colori;

montaggio del circuito n° 1 per la misura del valore 949b14j reale delle resistenze;

montaggio del circuito n° 2, un partitore di tensione, per misurare la caduta del potenziale nel circuito cambiando di volta in volta la resistenza inserita nel circuito così da ottenere una serie di dati per la costruzione di un grafico (la batteria genera corrente continua, il multimetro va impostato sul fondo scala DCV);

costruzione del grafico con la variazione dell'inverso del potenziale in funzione delle resistenze, per il calcolo della resistenza interna del multimetro e del potenziale ai capi della batteria;

costruzione del circuito n° 3 per la carica del condensatore, esso impiega a caricarsi circa 10 secondi (collegare con le giuste polarità il condensatore in quanto polarizzato);

costruzione del circuito n° 4 per lo studio delle cadute di potenziale ai capi del condensatore in funzione del tempo, cioè durante la scarica;

stima delle cadute di potenziale ogni tre secondi fino al raccoglimento di 25 valori;

costruzione del grafico con la variazione del logaritmo naturale del potenziale in funzione del tempo, per il calcolo della capacità del condensatore e del potenziale ai suoi capi (il condensatore genera corrente continua, il multimetro va impostato sul fondo scala DCV);

IL CONDENSATORE E I CIRCUITI MONTATI DURANTE L'ESPERIENZA

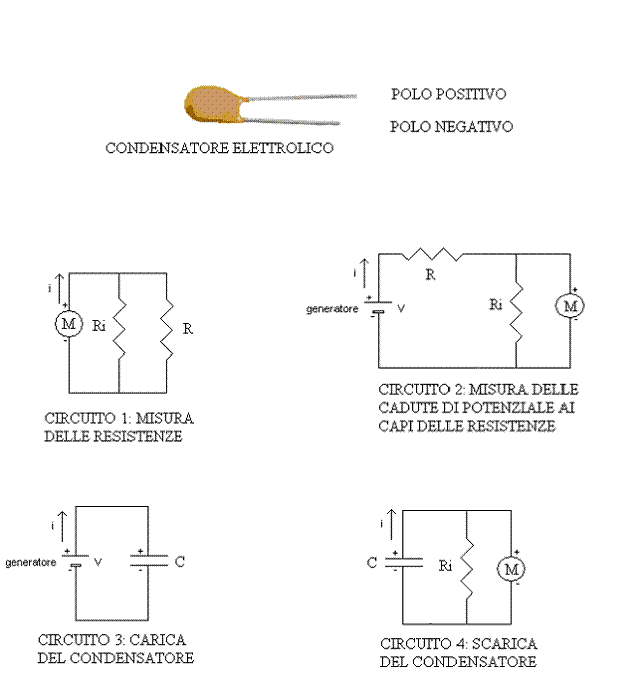
All'interno del quadrato tratteggiato è schematizzato il multimetro, rappresentato con la sua resistenza interna.

IL CONDENSATORE E IL CALCOLO DELLA SUA CAPACITÁ ELETTRICA

Lo scopo dell'esperienza è stato quello di determinare indirettamente la capacità di un condensatore elettrolitico.

Il condensatore è un dispositivo elettrico che permette di accumulare e conservare una quantità di energia potenziale elettrica. Esso è costituito da due conduttori laminari e paralleli, definiti armature, separati da un materiale isolante, cioè dielettrico. Se questo dispositivo è inserito in un circuito elettrico assieme ad un generatore di corrente, questo applicherà una differenza di potenziale, cioè un campo elettrico ai capi del condensatore che caricherà le piastre del condensatore con una carica proporzionale alla differenza di potenziale che genera il campo elettrico:

Q = C * ΔV

dove C è una costante caratteristica per ogni condensatore, definita capacità elettrica, che si misura in Farad: F. Questa costante esprime quindi la capacità che ha un conduttore di accumulare carica elettrica sulla sua superficie in funzione della differenza di potenziale applicata su di esso.

In base a questa relazione si nota che più la differenza di potenziale è alta più carica si depositerà sulle armature del condensatore.

Questa capacità è quindi calcolabile se si conosce la differenza di potenziale applicata e la carica che si è depositata sulle armature del condensatore.

Per caricare il condensatore c'è bisogno quindi di uno strumento che generi una differenza di potenziale, questa produrrà un campo elettrico all'interno del circuito che prenderà gli elettroni dal polo positivo del condensatore per trasferirli sull'armatura negativa. Questo processo durerà fintanto che le due armature si saranno caricate di una carica uguale e opposta tale che il condensatore abbia ai suoi capi una differenza di potenziale uguale a quella del generatore, a questo punto il passaggio di corrente all'interno del circuito si interromperà.

LA SCARICA DEL CONDENSATORE

Nella nostra esperienza non ci siamo avvalsi della relazione che lega la carica accumulata alla differenza di potenziale, per calcolare la capacità elettrica del nostro condensatore, ma abbiamo utilizzato la legge che descrive la scarica di un condensatore.

Se un condensatore carico è inserito in un circuito assieme ad un utilizzatore, cioè una resistenza, così da creare un circuito RC, esso assumerà la funzione di generatore in quanto comincerà a fornire corrente al circuito. La corrente sarà fornita fino a che le piastre del condensatore saranno scariche, in quanto gli elettroni che erano stati strappati dalla piastra positiva ritorneranno su di essa; a questo punto non ci sarà più una differenza di potenziale fra le piastre che possa determinare un flusso di cariche nel circuito. Prendendo come nullo il valore di una delle piastre, il potenziale dell'altra, che è uguale quindi alla differenza di potenziale, diminuirà nel tempo con un andamento esponenziale decrescente espresso dalla relazione:

V (t) = V₀ * e^-t/t t = R * C

dove V₀ è il potenziale del condensatore al tempo t = 0 s e t è la costante di tempo caratteristica del circuito RC in esame. Da questa legge deduciamo che se C aumenta t aumenterà e il condensatore impiegherà più tempo a scaricarsi, infatti se C è alta ci saranno più cariche sulle piastre del condensatore che dovranno essere fatte fluire nel circuito per scaricare il condensatore; se invece aumenta R le cariche del condensatore impiegheranno più tempo a percorrere il circuito determinando un allungamento del tempo di scarica.

Scrivendo la legge in forma logaritmica otteniamo una relazione che ci descrive l'andamento lineare decrescente del logaritmo del potenziale in funzione del tempo:

costruendo il grafico dell'andamento di lnV nel tempo, con i valori presi durante la scarica del condensatore, possiamo, tramite l'interpolazione dei dati, ricavarci i valori dell'intercetta e del coefficiente angolare della retta che meglio approssima l'andamento dei valori; e, attraverso questi, calcolarci il potenziale ai capi del condensatore, che sarà approssimativamente uguale a quello della batteria, e la capacità del condensatore:

C = lnV₀ V₀ = e^c

per applicare queste formule occorrerà conoscere il valore della resistenza inserita nel circuito RC. Siccome per misurare il potenziale abbiamo utilizzato un multimetro, che ha una sua resistenza interna molto elevata, non abbiamo dovuto inserire altre resistenze nel circuito. Inoltre dato l'elevato valore della resistenza del multimetro ci siamo permessi di trascurare la resistenza dei cavetti di collegamento che hanno una resistenza molto più bassa del multimetro, la quale dovrà essere quindi calcolata. È importante conoscere questo valore anche per la misura dei potenziali: in questa misura il multimetro è montato in parallelo così che attraverso esso non passa corrente, la quale deve passare solo attraverso l'utilizzatore. Ma perchè attraverso esso non passi corrente la sua resistenza deve essere elevata, idealmente infinita; siccome ciò non è possibile dobbiamo calcolare questo valore che, seppur in maniera minima, perturberà il passaggio di corrente e quindi le letture effettuate.

CALCOLO DELLA RESISTENZA INTERNA DEL MULTIMETRO

Per calcolare la resistenza interna del multimetro abbiamo dovuto trovare il modo di conoscere la differenza di potenziale ai suoi capi e di trovare una relazione che la legasse alla sua resistenza interna. Non potendo misurare direttamente il potenziale ai capi del multimetro, a causa della resistenza dei cavi che non è conosciuta, abbiamo costruito dei partitori di tensione con resistenze molto grandi in modo da poter trascurare quelle dei cavi.

In un partitore di tensione la differenza di potenziale totale è data da:

V₀ = (R + Ri) * I

dove R è la resistenza inserita nel circuito e Ri è la resistenza interna del voltometro; siccome ai capi della Ri c'è una differenza di potenziale V = Ri * I, possiamo dalla prima relazione scritta, ricavarci una legge che leghi il potenziale ai capi del multimetro alla resistenza inserita nel circuito, cambiata per ogni misura:

scrivendo la relazione in questo modo otteniamo un metodo per studiare l'andamento del potenziale all'interno del circuito; costruendo un grafico con questo andamento e ripetendo le operazioni di interpolazione, come sul primo grafico, possiamo ricavare il valore dell'intercetta e del coefficiente angolare della retta che meglio approssima l'andamento dei valori presi:

dal valore dell'intercetta possiamo ricavarci la tensione della pila, cioè quella esistente quando non ci sono altre resistenze inserite nel circuito; dal valore del coefficiente angolare ricaviamo il valore della resistenza interna se conosciamo la tensione della batteria.

VALORE DELLE RESISTENZE

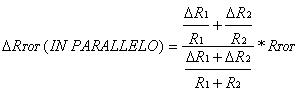
CADUTE DI POTENZIALE NEL CIRCUITO AL VARIARE DELLE RESISTENZE

²

VALORI PROVENIENTI DALL'INTERPOLAZIONE DEI VALORI DEL GRAFICO DELL'INVERSO DEL POTENZIALE, IN FUNZIONE DELLE RESISTENZE;

CALCOLO DELLA RESISTENZA DEL MULTIMETRO

retta a pendenza massima: c (0; 0.106) punto per il calcolo di m: (16230000; 0.281);

retta a pendenza minima:   c (0; 0.107) punto per il calcolo di m: (16230000; 0.277);

 

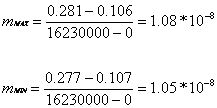
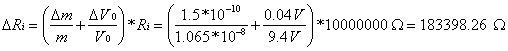
V₀ = (9.40 0.04) V

R_i = (10000000.00

CADUTE DI POTENZIALE NEL TEMPO

ERRORE SUL LOGARITMO NATURALE DEI POTENZIALI:

V

VlnV =   

V²

VALORI PROVENIENTI DALL'INTERPOLAZIONE DEI VALORI DEL GRAFICO DEL LOGARITMO NATURALE DEL POTENZIALE IN FUNZIONE DEL TEMPO;

CALCOLO DELLA CAPACITÁ DEL CONDENSATORE

retta a pendenza massima: c (0; 2.237) punto per il calcolo di m: (6; 2.210);

retta a pendenza minima:   c (0; 2.228) punto per il calcolo di m: (6; 2.203);

 

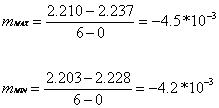
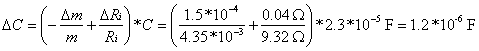
V₀ = (9.32 ± 0.04) V

C = (2.3*10^-5 10^-5) F = (23 ± 1) F

ANALISI DEI DATI E CONSIDERAZIONI PERSONALI

L'esperienza effettuata ci ha permesso di calcolare un valore, a nostro parere accettabile, per la capacità del condensatore. Possiamo affermare che è un buon valore innanzitutto perché questo presenta un'incertezza piccola e accettabile in quanto le misure sono state effettuate con uno strumento abbastanza preciso. In secondo luogo abbiamo potuto compiere diversi riscontri che hanno confermato le nostre ipotesi:

i grafici costruiti mostrano con un'approssimazione accettabile, gli andamenti ipotizzati sia per il logaritmo naturale dei potenziali durante la scarica, sia per l'inverso del potenziale al variare delle resistenze;

il valore del potenziale del generatore, calcolato per avere misure più precise, ricavato dal grafico dell'andamento dell'inverso del potenziale coincide, nei limiti dell'errore con quello nominale riportato sulla batteria;

il valore del potenziale del condensatore proveniente dallo studio del grafico per la scarica del condensatore, è approssimabile al potenziale del generatore con il quale dovrebbe in teoria coincidere a carica avvenuta.

STUDIO DELLA SCARICA:

Nel prelevare i dati per rappresentare la scarica del condensatore non abbiamo aspettato che il condensatore si scaricasse completamente: questo perché l'andamento del potenziale è lo stesso durante tutta la scarica, inoltre perché man mano che il potenziale tende a zero il multimetro non riesce più ad apprezzare le sue variazioni.

Questa stima di valori è stata preceduta da una carica e una scarica di prova, quest'operazione ci è stata utile per due motivi: abbiamo potuto impostare il giusto fondo scala e la giusta portata e abbiamo potuto osservare con quale velocità variava il potenziale così da poter fissare un giusto intervallo di tempo per prendere i valori del potenziale.

STUDIO DEI POTENZIALI AL VARIARE DELLE RESISTENZE:

Il circuito n° 2 è stato costruito sia con le resistenze forniteci sia con delle resistenze che abbiamo creato mettendo quelle date o in serie o in parallelo; questo per avere più valori da inserire nel grafico così da renderlo più preciso.

Un accorgimento preso nello studio di questo circuito è stato quello di aprirlo non appena si prendeva la misura di potenziale, ciò per non scaricare troppo la batteria.

Per ottenere misure precise abbiamo misurato con il multimetro il valore delle resistenze forniteci e di quelle create, infatti i valori riportati su queste non sono precisi, ma ci sono comunque stati utili per impostare la giusta portata per misurarli.