|
|
| |
Appunti delle lezioni di prof. Giuseppe Puggioni
a cura di M. Marras e B. Pettinelli
Se si ripartisce l’universo degli N studenti iscritti al I anno che hanno frequentato il Corso di Statistica in un dato anno accademico. in due categorie: A (studenti in sede) e B (studenti fuori sede o pendolari), si avranno due sub-universi composti rispettivamente da nA e da nB studenti per cui nA +nB=N.
La probabilità (p) di estrarre da N uno studente
residente è quindi ![]() e la probabilità (q)
di estrarre uno studente non residente è
e la probabilità (q)
di estrarre uno studente non residente è ![]() . Essendo
. Essendo ![]() e
e ![]() sarà p+q=1 in quanto
sarà p+q=1 in quanto ![]() . Ne consegue che essendo p+q=1 sarà q=1-p.
. Ne consegue che essendo p+q=1 sarà q=1-p.
Il fatto che p+q=1 sta ad indicare che se dagli N studenti se ne estrae uno, esso sarà certamente o della categoria A (in sede) o della categoria B (fuori sede o pendolare
Si supponga ora che l’universo degli studenti che hanno frequentato sia
composto da 50 individui di cui 25 della categoria A e 25 di quella B e si
voglia estrarre un gruppo di 5 studenti reinserendo dopo ogni estrazione
l’unità estratta. Ciò comporta che sia la numerosità dell’universo sia la sua
composizione secondo le due categorie A e B non si modificheranno nel corso
dell’estrazione dei 5 studenti che formeranno il gruppo che si vuole esaminare,
per cui la probabilità di estrarre ad ogni estrazione uno studente appartenente
alla categoria A sarà ![]() e quella di estrarre
uno studente appartenete alla categoria B
e quella di estrarre
uno studente appartenete alla categoria B ![]() .
.
È del tutto evidente che seguendo un tale modo di procedere:
a. il numero totale di gruppi che potranno essere
estratti sarà pari a ![]() Fra questi 32 gruppi,
essendo state estratte le singole unità una alla volta e quindi reinserite
prima di procedere all’estrazione successiva, è chiaro che vi saranno gruppi
composti dagli stessi studenti, ancorché estratti secondo differenti sequenze
di estrazione.
Fra questi 32 gruppi,
essendo state estratte le singole unità una alla volta e quindi reinserite
prima di procedere all’estrazione successiva, è chiaro che vi saranno gruppi
composti dagli stessi studenti, ancorché estratti secondo differenti sequenze
di estrazione.
b. . I 32 gruppi formeranno 6 insiemi ciascuno dei quali sarà composto da 0 studenti di tipo A e 5 di tipo B, da 1 studente di tipo A e 4 di tipo B, da 2 studenti di tipo A 313f52d e 3 di tipo B, e cosi via fino a 5 studenti di tipo A e 0 di tipo B. Da ciò discende che i cinque studenti estratti, qualunque essi siano, apparteranno certamente a uno di questi possibili gruppi.
La distribuzione della frequenza dei 6 gruppi possibili, ciascuno composto da 5 studenti secondo il numero di quelli appartenenti alla categoria A e alla categoria B, sarà data da:
1° gruppo: 0 studenti
di tipo A e 5 di tipo B = ![]()
2° gruppo: 1 studenti
di tipo A e 4 di tipo B = ![]()
3° gruppo: 2 studenti
di tipo A e 3 di tipo B = ![]()
4° gruppo: 3 studenti
di tipo A e 2 di tipo B = ![]()
5° gruppo: 4 studenti
di tipo A e 1 di tipo B = ![]()
6° gruppo: 5 studenti
di tipo A e 0 di tipo B = ![]()
Totale dei possibili gruppi 32
Da questa distribuzione si evince, ad esempio, che
l’evento 2 studenti di tipo A 313f52d e 3 di tipo B può realizzarsi in 10 modi diversi,
mentre l’evento che prevede che tutti e cinque gli studenti appartengano al
tipo A può verificarsi in un solo modo. Come si è già avuto occasione di
sottolineare si può osservare che il numero di gruppi che si possono realizzare
al variare di h, cioè del numero degli studenti di tipo A e quindi di quelli di
tipo B, essendo il gruppo composto da un numero dispari di studenti (5), cresce
fino ai valori di h 2 e 3 e cioè ![]() , per poi decrescere in modo simmetrico.
, per poi decrescere in modo simmetrico.
Volendo ora conoscere quale è la probabilità che si
verifichi ciascuno dei 6 possibili gruppi, ricordando quanto già si è avuto
modo illustrare a proposito della probabilità composta di eventi indipendenti,
facendo variare h da 0 a n questa sarà data da ![]() [1].
[1].
Essendo come già specificato p+q=1, applicando il
teorema della probabilità totale, sarà ![]() . In termini probabilistici ciò sta ad indicare, come per
altro già sottolineato, che è certo che si verificherà uno dei possibili
eventi rappresentando
. In termini probabilistici ciò sta ad indicare, come per
altro già sottolineato, che è certo che si verificherà uno dei possibili
eventi rappresentando ![]() tutto lo spazio campionario (Ω).
tutto lo spazio campionario (Ω).
La [1] prende il nome di distribuzione binomiale. Essa è una distribuzione teorica, discreta e finita.
È una distribuzione teorica in quanto fornisce quelle che teoricamente sono le probabilità che, dato n, si verifichino le varie possibili combinazioni di nA e di nB, è discreta in quanto h può assume solo valori discreti da 0 a n ed è finita essendo n finito.
Tornando al nostro esempio ipotetico in cui p e q sono
ambedue uguali a ![]() cioè 0,5, la
probabilità che hanno le singole
cioè 0,5, la
probabilità che hanno le singole ![]() , per h che assume i valori 0, 1 2, 3, 4 e 5, saranno date da :
, per h che assume i valori 0, 1 2, 3, 4 e 5, saranno date da :
![]() [probabilità che
tutti e cinque gli studenti non siano residenti]
[probabilità che
tutti e cinque gli studenti non siano residenti]
![]() [probabilità che si
abbia uno studente residente e quattro non residenti]
[probabilità che si
abbia uno studente residente e quattro non residenti]
![]() [probabilità che si
abbiano due studenti residenti e tre non residenti]
[probabilità che si
abbiano due studenti residenti e tre non residenti]
![]() [probabilità che si
abbiano tre studenti residenti e due non residenti]
[probabilità che si
abbiano tre studenti residenti e due non residenti]
![]() [probabilità che si
abbiano quattro studenti residenti e uno non residente]
[probabilità che si
abbiano quattro studenti residenti e uno non residente]
![]() [probabilità che
tutti e cinque gli studenti siano residenti]
[probabilità che
tutti e cinque gli studenti siano residenti]
Come la distribuzione di tutti i possibili
gruppi (campioni), anche la distribuzione di probabilità ottenuta è una
distribuzione simmetrica in quanto, essendo p=q, il prodotto ![]() per tutti i gruppi al
variare di h sarà sempre uguale a 0,55. In altri termini, per tutti
i valori di h da 0 fino a n, sarà sempre
per tutti i gruppi al
variare di h sarà sempre uguale a 0,55. In altri termini, per tutti
i valori di h da 0 fino a n, sarà sempre ![]() , per cui yh varierà solo al variare del valore di
, per cui yh varierà solo al variare del valore di
![]() .
.
Come per qualsiasi distribuzione anche la binomiale ammetterà una media e una varianza. Si dimostra, dimostrazione che stante il livello elementare di queste dispense non si ritiene di dover riportare, che esse sono, rispettivamente, date da:
m = np e s = npq
In riferimento al nostro esempio il numero medio di studenti residenti fra tutti i possibili gruppi sarebbe quindi di 2,5 (5 x 0,5) e s =5 x 0,5 x 0,5=1,25
La distribuzione binomiale per p=q gode delle seguenti proprietà:
è una distribuzione simmetrica con il massimo,
nel caso di n pari, in corrispondenza di ![]() , mentre nel caso di n dispari si avranno due massimi in
corrispondenza di
, mentre nel caso di n dispari si avranno due massimi in
corrispondenza di ![]() ;
;
a partire dal massimo o dai massimi, per i termini simmetrici, yh assumerà valori identici e decrescenti da entrambe le parti;
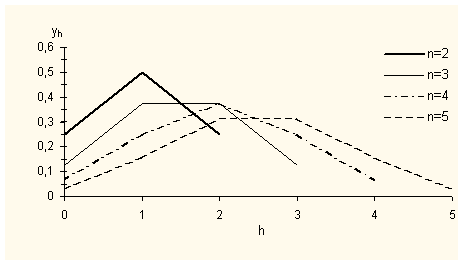
il massimo o i massimi (ovviamente per p costante) saranno sempre in corrispondenza dei valori di h indicati al punto 1, ma i valori di yh decrescono al crescere di n. Si avrà quindi una estensione della distribuzione in cui le yh, in riferimento ai valori estremi, assumeranno valori sempre più piccoli tendenti cioè a 0. In altri termini se si rappresentano in un diagramma i valori delle yh si può osservere che al crescere di n esso si spiana avvicinandosi sempre di più all’asse delle x, così come esemplificato nella Fig. 1[2];
Fig. 1 – Alcune distribuzioni binomiali per differenti n e p=q=0,5
Nel caso di p q, i valori delle yh danno luogo ad
una distribuzione asimmetrica il cui grado di asimmetria sarà tanto più
accentuato tanto maggiore sarà la diversità di p rispetto a q. Ciò significa
che, a parità di n, la forma della distribuzione dipende dai valori di p e di
q. Tornando al nostro ipotetico esempio se fra i 50 studenti i residenti
fossero 40 (gruppo A) e i non residenti 10 (gruppo B), per cui ![]() la nostra
distribuzione di probabilità sarebbe data da:
la nostra
distribuzione di probabilità sarebbe data da:
![]() [probabilità che
tutti e cinque gli studenti non siano residenti]
[probabilità che
tutti e cinque gli studenti non siano residenti]
![]() [probabilità che si
abbia uno studente residente e quattro non residenti]
[probabilità che si
abbia uno studente residente e quattro non residenti]
![]() [probabilità che si
abbiano due studenti residenti e tre non residenti]
[probabilità che si
abbiano due studenti residenti e tre non residenti]
![]() [probabilità che si
abbiano tre studenti residenti e due non residenti]
[probabilità che si
abbiano tre studenti residenti e due non residenti]
![]() [probabilità che si
abbiano quattro studenti residenti e uno non residente]
[probabilità che si
abbiano quattro studenti residenti e uno non residente]
![]() [probabilità che
tutti e cinque gli studenti siano residenti]
[probabilità che
tutti e cinque gli studenti siano residenti]
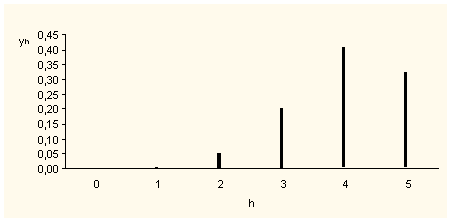
Come appare con tutta evidenza sia dai valori delle yh sia dalla Fig. 2, la distribuzione si caratterizza per una accentuata asimmetria negativa
Fig. 2 – Distribuzione binomiale per n=5, p=0,8 e q=0,2
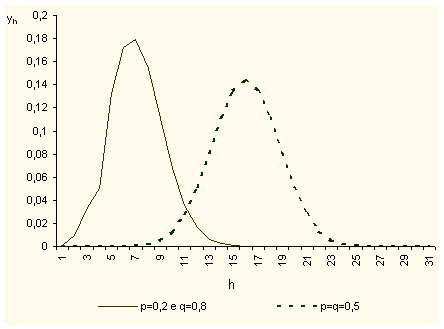
Si fa comunque presente che se p q, al crescere di n la distribuzione tende a caratterizzarsi come una distribuzione normale, con media e varianza date sempre dalla . Tale affermazione trova conferma nella Fig. 3 dove sono riportati i valori delle yh sempre nel caso di p 0,8 e q=0,2, ma per n=35. Dalla Fig. 3, infatti, si può notare che la distribuzione, a differenza del caso in cui n=5, si caratterizza per una asimmetria poco accentuata. In altri termini, tenendo costanti p e q, facendo aumentare n, anche nel caso di p q, la distribuzione tende sempre di più ad essere simmetrica e assimilabile alla distribuzione normale.
Da ciò discende che per n grande, situazione questa in cui sarebbe molto laborioso il calcolo delle yh, per determinare la probabilità che si verifichino le combinazioni non maggiori di un dato h o quelle relative a hi+1 - hi si può ricorre alla normale[3].
Per dare concretezza a quanto detto se, ad esempio, si
hanno 2000 studenti di cui 600 in possesso della maturità classica e 1400 in
possesso di un diverso diploma, per cui ![]() , e si estraggono a sorte 300 studenti, sarebbe laborioso
determinare la probabilità che si abbiano non meno di 35 studenti con la
maturità classica e 265 in possesso di un altro diploma di scuola secondaria. Per
la determinazione di tale probabilità si dovrebbe, infatti, calcolare le
probabilità per h da 0 a 35, che sarà data da:
, e si estraggono a sorte 300 studenti, sarebbe laborioso
determinare la probabilità che si abbiano non meno di 35 studenti con la
maturità classica e 265 in possesso di un altro diploma di scuola secondaria. Per
la determinazione di tale probabilità si dovrebbe, infatti, calcolare le
probabilità per h da 0 a 35, che sarà data da:
Fig. 3
2 - La distribuzione normale o distribuzione degli errori accidentali
Assai spesso osservando le distribuzioni di densità empiriche si può notare, come ad esempio nelle distribuzioni degli individui secondo l’altezza, che i casi estremi sono i più rari, mentre quelli centrali sono i più numerosi. Così se si eseguono numerose misure su di una medesima grandezza, a causa degli errori di natura accidentale che si possono commettere, è del tutto evidente che gli errori più piccoli saranno più frequenti di quelli più grandi. In altri termini si tratta di distribuzioni che partendo da valori piccolissimi o da 0, crescono fino a raggiungere un massimo e quindi diminuiscono fino a valori piccolissimi o a 0. In base a queste osservazioni, che si trovano, come ricorda il Leti, già accennate nel pensiero di alcuni filosofi dell’antica Grecia, prima de Moivre e successivamente, dopo oltre settanta anni, Gauss, che la chiamò, oltre che con il suo nome, curva degli errori accidentali, trovarono la funzione che poteva descrivere questi tipi di distribuzioni. Il nome di curva degli errori accidentali deriva dal fatto che, anche sperimentalmente, si è potuto verificare che le misure ripetute su di una stessa grandezza “si distribuiscono attorno ad un valore in modo che al crescere del valore assoluto dell’errore diminuisce la sua frequenza e che la frequenza di ciascun errore positivo è uguale a quella dell’errore negativo di pari valore assoluto”. Non può quindi che trattarsi di una curva campanulare simmetrica e il cui valore massimo si ha, in corrispondenza dell’errore 0 (cioè delle misure esatte) nell’asse delle x che dovrebbero registrare la massima frequenza.
L’equazione di questa curva è:
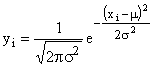 [1]
[1]
dove σ e μ, che sono i parametri della funzione, sono rispettivamente lo scostamento quadratico medio e la media aritmetica della distribuzione[5] e e (= 2,718181 . ) è la base dei logaritmi neperiani.
Fig. 4 – La curva normale
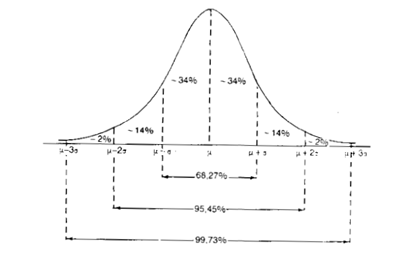
Figura ripresa da G. Leti, Statistica descrittiva
Alcune importanti caratteristiche della Curva normale:
l’ascissa del massimo, che coincide con la mediana e la moda, è μ;
essendo la ascissa del massimo uguale a μ per cui per xi = μ, sarà (xi – μ)2 = 0
e quindi e0 = 1, il
valore dell’ordinata del punto di massimo sarà uguale a 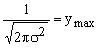 ;
;
è asintotica all’asse delle x, cioè quanto più ci si allontana dalla media, tanto più la curva si avvicina all’asse delle x; y sarà uguale a 0 solo per x uguale a +∞ e -∞;
le ascisse dei punti di flesso, nei punti cioè in corrispondenza dei quali la curva da concava diventa convessa, sono μ–σ e μ+σ (v. Fig. 4);
è simmetrica rispetto all’ordinata passante per xi = μ e cioè rispetto alla parallela all’asse y e passante per l’ascissa del punto di massimo (Fig.4). Questo è il motivo per cui necessariamente deve essere Me, = Mo = μ, come indicato al punto 1;
essendo le yi frequenze relative, l’area racchiusa dalla curva è uguale a 1 (v. numeratore della [1]);
l’area racchiusa dalla curva, dall’asse delle x e dalle due ordinate in corrispondenza di due punti xi e xh dà la frequenza relativa dei casi compresi nell’intervallo xi - -xh;
negli intervalli ; e ,, cade rispettivamente il 68,27%, il 95,45% e il 99,73% dei casi (v. Fig.4).
Essendo l’equazione della curva normale definita dai soli due parametri μ e σ, è del tutto evidente che, potendo ognuno di questi parametri assumere infiniti valori, nel piano esisterebbero infinito a due curve normali. Al variare di μ (che rappresenta il parametro di posizione) la curva si sposterà lungo l’asse delle x conservando la stessa forma (Fig.5), mentre al variare di σ (che rappresenta la dispersione) la curva assumerà una forma più appiattita se σ cresce, mentre se σ diminuisce, essa risulterà più ristretta (Fig. 6). Tale evidenza deriva dal fatto che all’interno degli intervalli di cui al punto 8 sopra indicato, dovrà essere sempre compreso lo stesso numero di casi. Se varieranno contemporaneamente sia μ che σ si avrà sia una traslazione sia un cambiamento di forma (Fig. 7).
Fig 5
B A
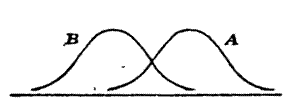
μA ≠ μB e σA = σB
Fig. 6
A B
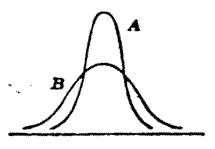
μA = μB e σA ≠ σB
Fig. 7
A B
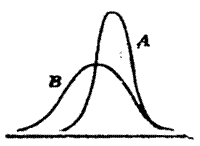
μA ≠ μB e σA ≠ σB
Nelle distribuzioni empiriche è pressoché impossibile avere una curva continua. Al massimo essa sarà data da un istogramma con le basi dei singoli rettangoli molto piccole (ad esempio la rappresentazione grafica delle altezze rappresentate non per centimetri, ma per millimetri). È comunque immaginabile, aumentando ovviamente il numero dei casi osservati, di ridurre sempre di più l’intervallo xi-xi+1,, fino a farlo tendere a 0, per cui tendendo a 0 anche le basi dei rettangoli dell’istogramma, la curva tenderà ad essere continua.
Da quanto detto risulta quindi che la Curva normale è una distribuzione teorica continua e illimitata in quanto copre tutto l’asse reale da +∞ a -∞. Questa ultima caratteristica, che ha senso solo sotto un profilo strettamente teorico, non è rilevante sul piano pratico in quanto, come si è avuto modo di sottolineare, già nell’intervallo μ ± 3σ è contenuto il 99,73% del totale dei casi[6].
Va subito precisato che non tutte le curve che assumono una forma campanulare, sono delle curve normali come quelle ad esempio riportate nelle Figg 8 e 9. Infatti si possono avere curve, che hanno la stessa media e lo stesso scostamento quadratico medio, che sono o più appuntite, dette ipernormali, (Fig. 8) o più appiattite, dette iponormali (Fig. 9).
Fig. 8
-2σ -σ μ +σ +2σ +3σ
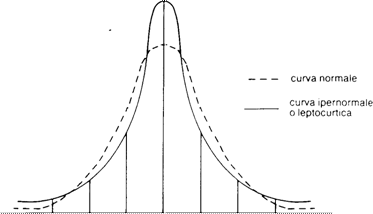
Fig. 9
-2σ -σ μ +σ +2σ +3σ
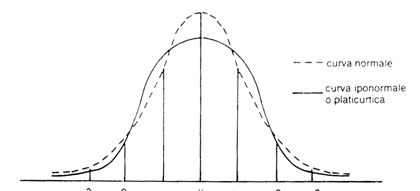
A questo punto, data una distribuzione empirica simmetrica e campanulare, il problema è quello di stabilire se si tratta di una curva normale oppure una ipernormale o iponormale e, in qusti ultimi due casi, misurare la sua anormalità (curtosi).
Nei casi concreti, nei quali quindi le distribuzioni sono rappresentate da curve campanulari “tendenzialmente” simmetriche, come sottolinea Leti, queste sono definite “da un insieme di punti discreto e limitato e non da una curva continua e illimitata. [Nel concreto] si cade poi nelle stesse inesattezze che sono state messe in luce a proposito delle misure di asimmetria: se una distribuzione è normale, necessariamente alcune caratteristiche (in numero finito) assumono determinati valori, ma non è detto che sia sufficiente affinché una curva sia normale che le caratteristiche assumano tali valori; lo stesso può dirsi per l’ipernormalità e l’iponormalità”.
Fatta questa premessa e tenuto conto anche di quanto già detto a proposito delle caratteristiche della curva normale, per decidere se una distribuzione è normale, dopo aver accertato che è simmetrica attraverso gli indici Sk (skewness di Peearson), b di Pearson e g di Fisher, che devono essere tutti uguali a 0[7], si deve verificare la sua normalità, e se questa non c’è, l’ipernormalità e l’iponormalità. A tal fine ci si deve accertare se sono soddisfatte questa condizioni:
1 - per gli intervalli:
a. x , p1 = 68,27%
b. x , p2 = 95,45%
c. x ; p2 = 99, 73%
Se si è in presenza di una distribuzione normale o molto prossima alla normale, dopo aver calcolato p1, p2, e p3 nella distribuzione empirica, si verifica se negli intorni e è racchiusa una identica percentuale di casi sopra indicata. In caso contrario se p1 > 68,27%, p2 < 95,45% e p3 > 99,73%, significa che la distribuzione è ipernormale; se invece p1 < 68,27%, p2 > 95,45% e p3 < 99,73%, significa che la distribuzione è generalmente iponormale.
2 - Se l’indice di eccesso di curtosi di Pearson b è uguale a 3: Cioè se:

Se b è maggiore di 3 la distribuzione è ipernormale, se è minore di 3 è iponormale e, ovviamente, se è uguale a 3 è normale. Posto g b -3, ne consegue che si avrà normalità se g = 0, ipernormalità se g > 0 e iponormalità se g <
3 - Se
il rapporto tra il doppio della varianza e il quadrato dello scostamento medio
semplice dalla media aritmetica (![]() ) è uguale a p (=3,14 . .). In termini analitici se
) è uguale a p (=3,14 . .). In termini analitici se
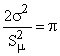
Se 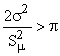 la distribuzione è
ipernormale, se invece
la distribuzione è
ipernormale, se invece 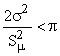 la distribuzione è
iponormale.
la distribuzione è
iponormale.
Così come, anche durante le lezioni, si è avuto modo di specificare, dovendo verificare se una data distribuzione possa ritenersi o meno normale, è opportuno calcolare più indicatori che ne misurano sia l’asimmetria che la curtosi. Ciò perché i dati forniti da questi indici non sempre sono concordi. Ne consegue che, solo osservando i valori di più indici, è possibile prendere una decisione circa la normalità o la non normalità di una data distribuzione empirica. (v. a questo proposito Leti a pagg. 614 e 615).
Va tenuto presente che essendo la normale una curva continua, in riferimento ad ogni singolo punto dell’asse delle x la corrispondente frequenza sarà uguale a 0, in quanto, passando dal discreto al continuo, la base dei rettangoli dell’istogramma tende a 0. Ne consegue, quindi, che è possibile determinare la frequenza dei casi solo in riferimento ad un intervallo ancorché piccolo: fino a xi; oppure xi - xi+1.
Sempre per il fatto che la curva normale è continua per la determinazione della frequenza fino a xi o da xi a xi+1 si dovrebbe calcolare l’integrale della sua funzione, che nel primo caso (frequenza cumulata fino a xi) sarà dato da:
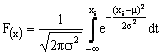 [2]
[2]
e nel secondo caso (frequenza da xi a xi+1) da:
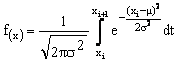
Per la determinazione dei valori della [2] o della [3] non è però necessario conoscere quelle nozioni di analisi matematica relative alla risoluzione degli integrali, in quanto, è sufficiente procedere alla standardizzazione delle xi[8]. In base ai valori di vi così ottenuti, i valori sia della [2] che della [3] sono ricavabili ricorrendo alla tavola degli integrali della curva normale standardizzata, come illustrato negli esempi.
Esempi di utilizzazione della tavola in cui sono riportate, in termini relativi, le aree sottese alla curva normale standardizzata oltre +vi e - vi.
1° Esempio
Rifacendoci alla Tab. 11 relativa alla distribuzione degli iscritti alla leva secondo la statura (v. Leti a pag. 614) da cui risulta che l’altezza media degli iscritti alla leva è pari a 172,73 cm e σ = 6,79, se si suppone che tale distribuzione sia normale e di conoscere di questa distribuzione solo μ e σ, la tavola della curva normale standardizzata ci consente di rispondere, ad esempio, a domande del tipo:
1 - quale è la percentuale degli iscritti alla leva che sono alti non più 163 cm?
2 - quale è la percentuale degli iscritti alla leva che hanno una altezza non inferiore a 173 cm e non superiore a 176 cm?
Nel primo caso si procede dapprima a trasformare 173
cm nel corrispondente punto v, nel seguente modo: ![]()
Attraverso la tavola della curva normale standardizzata in corrispondenza di v = 1,44 si legge che l’area sottesa dalla curva, cioè la frequenza relativa dei casi, oltre v = 1,44 è pari a 0,074934.
Questo dato, sempre che sia vera l’ipotesi che la distribuzione sia normale, ci dice che il 7,49% degli iscritti alla leva ha una statura non superiore a 163 cm.
N.B. Il risultato ottenuto deriva dal fatto che essendo la curva normale simmetrica, l’area oltre vi nella metà a destra della curva è uguale a quella fino allo stesso valore di vi nell’altra metà a sinistra
Nel secondo caso si procede in modo analogo: ![]() e
e ![]() . Sempre in base alla tavola della normale standardizzata, risultando
l’area sottesa alla curva oltre v1 pari a 0,4840061 e oltre v2
di 0,315614, ed essendo:
. Sempre in base alla tavola della normale standardizzata, risultando
l’area sottesa alla curva oltre v1 pari a 0,4840061 e oltre v2
di 0,315614, ed essendo:
si deduce, in base all’ipotesi iniziale di normalità della distribuzione, che il 16,8% degli individui ha una altezza compresa tra 173 e 176 cm.
2° Esempio
Se la pensione media è di 1500 € e σ = 300 € e supposto anche in questo caso che la distribuzione delle pensioni sia normale, si chiede quale è la percentuale di pensionati:
1 - che gode di una pensione mensile non inferiore a 1600 € e non superiore a 2000 €
2 - che percepisce una pensione mensile inferiore a 300 €
Si desidera sapere, inoltre, quale sia la classe di pensione intorno alla media che racchiude il 72% dei pensionati.
Nel primo caso essendo ![]() ;
; ![]() , dalla tavola della curva standardizzata si hanno in
riferimento a v1 e a v2 rispettivamente i seguenti valori
0,091759 e 0,047460. Essendo queste le frequenze relative oltre v1 e
v2, quelle comprese tra questi due punti della curva, saranno date
da 0,091759 - 0,047460 = 0,044299. Risulta, quindi, che la percentuale di
pensionati che percepiscono una pensione mensile compresa tra 1600 e 2000 € è
pari al 4,4%.
, dalla tavola della curva standardizzata si hanno in
riferimento a v1 e a v2 rispettivamente i seguenti valori
0,091759 e 0,047460. Essendo queste le frequenze relative oltre v1 e
v2, quelle comprese tra questi due punti della curva, saranno date
da 0,091759 - 0,047460 = 0,044299. Risulta, quindi, che la percentuale di
pensionati che percepiscono una pensione mensile compresa tra 1600 e 2000 € è
pari al 4,4%.
Per quanto attiene al secondo quesito essendo ![]() , dalla tavola si ricava che in corrispondenza di v = 4,0
l’area sottesa dalla curva (=frequenza relativa dei casi) è uguale a 0,000032,
evidenza questa che ci dice che solo il 3,2 per 100 mila pensionati gode di una
pensione inferiore a 300 €. Si fa notare che, come in questo caso, essendo la
curva simmetrica la frequenza oltre v è la stessa che è racchiusa fino a –v (v.
figura riportata in calce alla tavola delle aree sottese alla curva normale
standardizzata).
, dalla tavola si ricava che in corrispondenza di v = 4,0
l’area sottesa dalla curva (=frequenza relativa dei casi) è uguale a 0,000032,
evidenza questa che ci dice che solo il 3,2 per 100 mila pensionati gode di una
pensione inferiore a 300 €. Si fa notare che, come in questo caso, essendo la
curva simmetrica la frequenza oltre v è la stessa che è racchiusa fino a –v (v.
figura riportata in calce alla tavola delle aree sottese alla curva normale
standardizzata).
Per rispondere alla terza domanda con cui si chiede
quale sia l’intervallo entro cui si trova il 72% dei pensionati, è necessario identificare
quale sia il punto v in corrispondenza della metà della frequenza relativa 0,72
(= 0,36). Fornendo la tavola l’area oltre
v, il suo valore va ricercato in corrispondenza di 0,5 - 0,36 = 0,14. Dalla
tavola si ricava che approssimativamente[9]
in corrispondenza di tale area v è pari a 1,08. Essendo ![]() , μ = 1500 e σ = 300, l’intervallo intorno alla
media in cui si trova il 72% dei pensionati sarà dato da:
, μ = 1500 e σ = 300, l’intervallo intorno alla
media in cui si trova il 72% dei pensionati sarà dato da:
![]() e
e ![]()
per cui :
![]()
![]()
Il risultato ottenuto sta ad indicare che il 72% dei pensionati ha una pensione compresa tra un minimo di 1176 e 1824 €.
|
- vi 0 +vi Aree sottese alla curva normale standardizzata oltre ±vi |
||||||||||||
|
vi |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Si ricorda che il prodotto di potenze aventi per base la stessa base è uguale ad una potenza che ha per base la stessa base e per esponente la somma degli esponenti
La fig. 1 dovrebbe essere rappresentata con un diagramma ad aste, perché i valori di xh sono definiti solo per valori interi. Si è data continuità per meglio evidenziare le diverse distribuzioni.
Si fa presente che nei casi in cui p q, e p<0,1 (evento raro) e n>50, la distribuzione binomiale non tende ad approssimarsi alla normale, ma alla distribuzione di Poisson, distribuzione questa che non sarà trattata nell’ambito di questo corso
Dovendo determinare la probabilità di avere non meno di 35 studenti in possesso della maturità classica, questa, trattandosi di eventi incompatibili, sarà data dalla somma delle singole probabilità da h=0 a h=35.
Da ciò deriva che se una distribuzione è normale e se di questa si conoscono solo μ e σ è possibile ricostruire l’intera distribuzione
Il fatto che il suo campo di esistenza si estenda da +∞ a -∞ comporta che, in riferimento agli errori accidentali, teoricamente e seppure con una probabilità infinitamente piccola e tendente a 0 si dovrebbero poter osservare errori, sia in senso positivo che negativo, infinitamente grandi
Si ricorda che la standardizzazione di una distribuzione si ottiene
sostituendo alle xi le vi
(o come indicato in altri manuali zi ) date da ![]() . Si ricorda inoltre che così operando si trasforma una data
distribuzione, qualunque essa sia, in una distribuzione sempre dello stesso
tipo avente media uguale a 0 e σ uguale a 1. Così operando, essendo le
modalità del carattere espresse da puri numeri e non più secondo una data unità
di misura, è possibile confrontare distribuzioni secondo caratteri diversi,
come, ad esempio, le distribuzioni di una popolazione secondo i pesi e secondo
le altezze.
. Si ricorda inoltre che così operando si trasforma una data
distribuzione, qualunque essa sia, in una distribuzione sempre dello stesso
tipo avente media uguale a 0 e σ uguale a 1. Così operando, essendo le
modalità del carattere espresse da puri numeri e non più secondo una data unità
di misura, è possibile confrontare distribuzioni secondo caratteri diversi,
come, ad esempio, le distribuzioni di una popolazione secondo i pesi e secondo
le altezze.
L’approssimazione è dovuto al fatto che non sempre nella tavola si trova esattamente il valore cercato, valore che è compreso tra due valori consecutivi (l’area pari a 0,14 si trova in corrispondenza del punto compreso tra v =1,08 e v=1,09. Nel nostro caso è stato assunto v=1,08 in quanto l’area sottesa dalla curva oltre questo punto è la più prossima a 0,14. Per v=1,09 infatti essa sarebbe pari a 0,137857. Volendo avere con precisione il punto v in corrispondenza di 0,14 si dovrebbe procedere al suo calcolo per parti proporzionali. Si fa presente che i sofware attualmente disponibili consentono di avere con precisione sia quale è l’area sottesa dalla curva per qualsiasi valore di v sia quale è il valore di v per qualsiasi porzione di area.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025