|
|
| |
ANALISI DI CONTABILITA' MULTIPRODOTTO
Attraverso il modello matematico di impresa che abbiamo definito DIAGRAMMA DI REDDITIVITA' (il diagramma raramente viene disegnato in quanto la struttura di costo e ricavo di una impresa non viene rappresentata graficamente) nel caso MONOPRODOTTO con le curve rappresentate dal ricavo totale RT e dal costo totale CT, ciascuna avente una sua espresione analitica pari a:
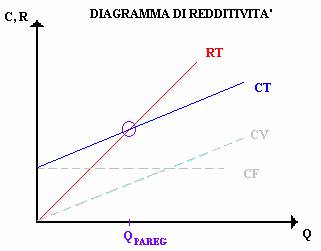 RT = p Q
RT = p Q
dove p rappresenta il prezzo mentre Q è il volume di produzione del prodotto.
CT = CV + CF = v Q + CF
dove v è il costo variabile unitario del prodotto, Q è il volume di produzione del prodotto, CV è il costo variabile del prodotto e CF è il costo fisso del prodotto.
Vediamo di capire come funziona questo modello, ossia qual è l'input 858j93i e l'output dell'impresa; l'input, cioè le variabili che possiamo controllare nell'impresa sono LE LEVE DI PRODUZIONE
LEVE DI PRODUZIONE:
In output avremo LA REDDITIVITA' misurabile attraverso
REDDITIVITA':
Il lavoro del manager è modificare le grandezze di input, ossia agisce sulle leve di produzione per migliorare o evitare che gli indicatori di redditività peggiorino molto. Ricordiamo che RO e MDCT sono variabili al variare del volume di produzione Q mentre mcu rimane costante al variare del volume di produzione Q per cui esso è una misura unitaria, intrinseca della redditività (se l'impresa preferisce una prospettiva a breve termine privilegia il risultato operativo, mentre a lungo termine potrebbe essere più importante mantenere alto il mcu perché se poi il volume di produzione aumenta perché aumenta la domanda e ci troveremo con una area degli utili maggiore se il MDCT è rimasto tale). A volte però bisogna decidere al di là del modello matematico osservando l'economia, il mercato, ecc.
Esiste la possibilità di trasformare i costi fissi CF in costi variabili CV e ciò significa abbassare la retta dei costi fissi CF per cui far scendere la retta dei costi totale CT ma aumentare la pendenza di CT; anche in questo caso a parità di volume di produzione e altri fattori; in questo punto il risultato operativo RO è lo stesso però al crescere o diminuire del volume di produzione Q diminuisce il mcu e il punto di pareggio QPAREG si sposta verso sinistra, l'area degli utili diventa più stretta; nei momenti di economia instabile, di crisi, si preferisce tale operazione perché pur diminuendo in generale la redditività si migliora il rischio cioè il punto di pareggio QPAREG si sposta e i profitti diminuiscono più lentamente mentre in momenti di economia più stabile è conveniente una struttura con molti costi fissi (sempre con il volume di produzione Q che aumenta) che è più redditizia.
Passiamo alla struttuta MULTIPRODOTTO e consideriamo l'esmpio di una falegnameria; il modello matematico non cambia ma varia la distinzione tra costi DIRETTI e INDIRETTI. Consideriamo un prodotto P1(ad esempio dei tavoli) caratterizzato dall'avere dei ricavi totali RT1, dei costi variabili CV1 e dei costi fissi CF1 e alla fine abbiamo il risultato operativo RO. Affianchiamo un prodotto P2(ad esempio delle sedie) e ci chiediamo come cambia la struttura di costi e ricavi in generale. Il ricavo totale lo possiamo distinguere dall'ammontare del ricavo di un prodotto da quello di un altro prodotto perché ciascun prodotto avrà un prezzo p1 e p2 con quantità di produzione che possiamo distinguerle in Q1 e Q2, quindi:
|
P1(tavoli) |
P2(sedie) |
|
RT1 = p1Q1 |
RT2 = p2Q2 |
|
|
|
|
|
|
Per cui avremo due
diagrammi di redditività per ciò che concerne la retta dei ricavi totali;
vediamo i costi variabili CV se possiamo distinguerli per ciascun prodotto(pensiamo
come costo variabile alle materie prime); ricordiamo che il costo variabile CV
è pari a vQ dove v è il costo variabile unitario e Q il il volume di produzione
e allo stesso modo il costo variabile unitario è pari a CUNITq dove costo
unitario; la quantità di produzione possiamo distiungurla in Q1 e Q2 (ad
esempio 100 tavoli al mese e 200 sedie al mese); per il costo unitario CUNIT
(pensiamo alla materia prima legno) esso sarà lo stesso per entrambi i prodotti
mentre per il consumo q esso sarà specifico per ogni prodotto(perchè, ad
esempio, saranno di più gli sprechi per la sedie oppure si deve lavorare di più
per la sedia); in generale v = ![]() se il prodotto è
costituito da più materie prime(se la sedia è formata da legno e metallosi deve
inserire il costo variabile unitario del legno e del metallo); in generale
possiamo distinguere i costi variabili unitario v perché ogni prodotto ha un
proprio consumo q di ciascuna materia prima quindi distinguiamo in CV1
e CV2 per cui(in un'impresa il parametro più difficile da misurare è
il consumo q di risorse variabile da prodotto a prodotto, ossia quanto legno
sta nella sedie e anche nella sedia e si effettua non solo pesando il legno ma
bisogna misurare la quantità di materia prima che viene scaricata dal magazzino
per sapere quanta quantita viene sprecata per produrre la sedia o il tavolo e
si ricava quanti Kg per tavolo o per sedia)
se il prodotto è
costituito da più materie prime(se la sedia è formata da legno e metallosi deve
inserire il costo variabile unitario del legno e del metallo); in generale
possiamo distinguere i costi variabili unitario v perché ogni prodotto ha un
proprio consumo q di ciascuna materia prima quindi distinguiamo in CV1
e CV2 per cui(in un'impresa il parametro più difficile da misurare è
il consumo q di risorse variabile da prodotto a prodotto, ossia quanto legno
sta nella sedie e anche nella sedia e si effettua non solo pesando il legno ma
bisogna misurare la quantità di materia prima che viene scaricata dal magazzino
per sapere quanta quantita viene sprecata per produrre la sedia o il tavolo e
si ricava quanti Kg per tavolo o per sedia)
|
P1 |
P2 |
|
RT1 = p1Q1 |
RT2 = p2Q2 |
|
CV1 = v1Q1 = CUNITq1Q1 |
CV2 = v2Q2 = CUNITq2Q2 |
|
|
|
Consideriamo adesso i costi fissi se possiamo separarli o meno. Ribadiamo il fatto che i costi variabili coincidono con i costi diretti CV = CDIRETTI mentre i costi fissi coincidono con i costi indiretti CF = CINDIRETTI per cui essendo i costi fissi di tipo indiretti essi non sono costi impiegati nel proceso produttivo, per cui non sono materie prime, lavoro, manodopera diretta, ma sono l'illuminazione, lo stipendio, l'affitto dello stabilimento ed altro. Ad esempio l'affitto dello stabilimento non possiamo dire che riguarda di più un prodotto invece che un altro quindi non possiamo operare un RIPARTIZIONE:
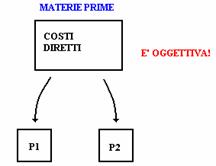
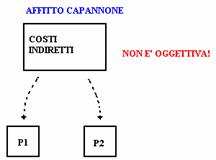
Se consideriamo dei costi diretti come le materie prime(è una risorsa, mentre P1 e P2 sono i prodotti), l'operazione di affermare che una parte del totale sono stati assorbiti dal prodotto P1 e la rimanente parte dal prodotto P2 si effettua in modo analitico perché si sa quanta materia prima è stata usata per un prodotto e per un altro per cui tale operazione è di misura OGGETTIVA. Al contrario se si vuole ripartire un costo indiretto, ad esempio l'affitto del capannone e lo si vuole ripartire fra i due prodotti, questa operazione è NON OGGETTIVA perché non esiste nessun modo oggettivo per capire quanto il prodotto ha assorbito; ad esempio si potrebbe ripartire a metà oppure il 70% al prodotto P1 perché costa di più oppure altro. In definitiva l'operazione di ripartizione dei costi indiretti è soggettiva; nell'analisi CVR diremo che i costi fissi sono dei costi COMUNI per cui non possiamo separarli fra i due prodotti ma vanno attribuiti all'intera azienda.
|
P1 |
P2 |
|
RT1 = p1Q1 |
RT2 = p2Q2 |
|
CV1 = v1Q1 = CUNITq1Q1 |
CV2 = v2Q2 = CUNITq2Q2 |
|
CFCOMUN |
|
In realtà esistono due tipi di costi fissi:
Vediamo come sarà la struttura di costo in termini di leve di produzione e in termini di misure di redditività. In termini di leve di produzione abbiamo qualche differenza nel senso che tre sono specifiche per ogni prodotto mentre una è comune (CF)
|
Prodotto P1 |
Prodotto P2 |
|
RT1 = p1Q1 |
RT2 = p2Q2 |
|
CV1 = v1Q1 = CUNITq1Q1 |
CV2 = v2Q2 = CUNITq2Q2 |
|
CFCOMUN |
|
|
LEVE DI PRODUZIONE |
|
|
p1 |
p2 |
|
v1 |
v2 |
|
CF |
|
|
Q1 |
Q2 |
In termini di misure di redditività(di profitto) abbiamo qualche differenza nel senso che due sono specifiche per ogni prodotto mentre una è comune (RO) perché i costi fissi sono comuni per cui esiste il risultato operativo dell'intera produzione e non un solo prodotto.
|
Prodotto P1 |
Prodotto P2 |
|
RT1 = p1Q1 |
RT2 = p2Q2 |
|
CV1 = v1Q1 = CUNITq1Q1 |
CV2 = v2Q2 = CUNITq2Q2 |
|
CFCOMUN |
|
|
MISURE DI REDDITIVITA' |
|
|
MDCT1 = RT1 - CV1 |
MDCT2 = RT2 - CV2 |
|
mcu1 = p1 - v1 |
mcu2 = p2 - v2 |
|
RO = RT1 + RT2 - CV1 - CV2 - CFCOMUN |
|
Quindi la misura di redditività potenziale(intrinseca, individuale) del singolo prodotto può essere misurata per ogni prodotto per cui è possibile confrontare la redditività intrinseca di ciascun prodotto. Alla domanda qual è il prodotto più redditizio possiamo rispondere sulla base delle misure di redditività: per confrontare più prodotti non possiamo usare il risultato operativo RO perché esso corrisponde all'utile complessivo di tutti i prodotti a fine semestre o trimestre od altro ma si deve usare o il margine di contribuzione totale MDCT o il margine di contribuzione unitario mcu; cioè formalmente
![]() i
i ![]() [1, n]: MDCTi = RTi - CVi =
(pi - vi)Qi = mcuiQi
[1, n]: MDCTi = RTi - CVi =
(pi - vi)Qi = mcuiQi
mcui = pi - vi
(per saper il costo variabile unitario, ad esempio degli spaghetti considero tutti i costi variabili del solo prodotto spaghetto e li divido per il volume di produzione della pasta per cui ad esempio il prezzo p è 1euro al kg mentre il costo variabile unitario è 0.60 euro al kg quindi il mcu degli spaghetti vale p - v 0.40 euro al kg, poi allo stesso modo calcolo il mcu dei sughi, poi quello dei biscotti e così via)
Noti i valori di MDCTi oppure mcui posso confrontarli: dal confronto verrà fuori che il prodotto più reditizio risulta quello che ha il mcu PIU'ALTO. Questa redditività, osservando il grafico, significa il prodotto che rende l'area degli utili più grande in quanto le rette sono più divergenti; ciò per quel che riguarda la redditività intrinseca ma non è detto che tale prodotto contribuisca positivamente all'utile e cioè se si produce secondo una quantità Q1 allora si ottiene un risultato operativo RO utile
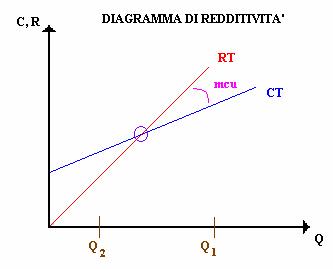 mentre se si produce secondo una quantità Q2 il risultato
sarà negativo; quindi per capire oltre alla redditività intrinseca anche la
redditività complessiva calcoliamo il margine di contribuzione totale MDCT di
tale prodotto; supponiamo Q pari a
mentre se si produce secondo una quantità Q2 il risultato
sarà negativo; quindi per capire oltre alla redditività intrinseca anche la
redditività complessiva calcoliamo il margine di contribuzione totale MDCT di
tale prodotto; supponiamo Q pari a
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026