 |  | |
|
| | |
|
| |
1. LE RELAZIONI FONDAMENTALI
Una delle più semplici ed efficaci descrizioni del funzionamento di un'impresa è quella che considera i legami tra i costi sostenuti, i volumi produttivi realizzati e i risultati economici conseguiti. Sebbene le relazioni tra queste grandezze siano, in realtà, piuttosto complesse, esse possono essere convenientemente presentate sotto forma lineare. Detta, infatti, Q la quantità di prodotto finito realizzata, in un determinato periodo di tempo, da una qualsiasi impresa i costi di produzione possono essere espressi come una funzione lineare di Q:
Costi di produzione = CF + cvu * Q
dove:
Anche i ricavi di vendita possono essere espressi come funzione lineare della quantità prodotta:
Ricavi di vendita = p * Q
dove p è il prezzo di vendita di un'unità di prodotto finito.
Ne discende che il profitto conseguito dall'impresa, cioè la differenza tra i ricavi di vendita e i costi di produzione, diventa anch'esso funzione lineare della quantità prodotta:
Profitto = p * Q - cvu * Q - CF
e raccogliendo i fattori comuni:
Profitto = (p - cvu) * Q - CF
La differenza (p - cvu) è chiamata margine di contribuzione unitario (mcu).
Il margine di contribuzione unitario rappresenta il beneficio economico netto che ogni singola vendita apporta all'impresa; questa differenza è, innanzitutto, destinata alla copertura dei costi fissi, di quei costi, cioè, che l'impresa dovrà sostenere in ogni caso, indipendentemente dalla produzione realizzata. Solamente dopo aver coperto tutti i costi fissi questi margini si trasformano in profitti effettivi.
Il prodotto mcu * Q è anche detto margine di contribuzione totale (MCT).
Possiamo così riscrivere la (1) nella forma seguente:
Profitto = MCT - CF
Sovente, la maggior parte se non la totalità dei costi fissi è costituita da sunk cost, cioè da quote di costi già sostenuti dall'impresa per realizzare investimenti in risorse prive di costo opportunità, cioè di valore di realizzo sul mercato o di valore utile in altri impieghi. Pur trattandosi di costi in senso contabile, queste quote di 'costi affondati' non assumono rilevanza sotto il profilo finanziario, essendo già stati sostenuti. In tal caso, l'intero margine di contribuzione rappresenta, per l'impresa, un cash flow che gli economisti chiamano quasi-rendita.
2. LE APPLICAZIONI PRATICHE
L'equazione (1) costituisce il punto di partenza dell'analisi costi/volumi/risultati. L'analisi offre risposte a domande di questo tipo:
a) quale livello minimo di vendite garantirà all'impresa almeno un risultato economico non negativo?
b) dato un obiettivo di profitto pari a U, per quale livello di produzione (e vendit 939d39j a) sarà possibile raggiungerlo?
c) dato un livello produttivo pari a Q, per quale prezzo di vendita sarà possibile ottenere almeno un risultato economico non negativo?
Consideriamole una per una.
a) Il punto di pareggio
Il problema è quello, classico, di determinazione del cd. punto di pareggio o break-even point (BEP), di quel livello di vendite, cioè, che consente all'impresa, attraverso la realizzazione dei margini di contribuzione, l'integrale copertura dei costi fissi.
Posto nella (1) il profitto pari a zero,
mcu * Q - CF = 0
e risolvendo per Q, otteniamo:
Quantità di pareggio =
DETERMINAZIONE DEL BREAK-EVEN POINT
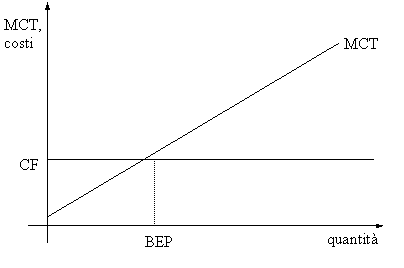
Se invece ci interessa conoscere il livello dei ricavi (fatturato) necessario a conseguire il pareggio economico è sufficiente moltiplicare entrambi i membri della (2) per il prezzo:
Fatturato di pareggio
dove il rapporto esprime la frazione del prezzo di vendita che, una volta coperti i costi variabili, è destinata alla copertura dei costi fissi e alla realizzazione di un profitto. Si tratta di un valore compreso tra 0 (quando p = cvu) e 1 (quando cvu = 0). Come vedremo, il rapporto in oggetto costituisce un indicatore fondamentale per descrivere la struttura dei costi di un'impresa.
DETERMINAZIONE GRAFICA DEL FATTURATO DI PAREGGIO
(1) con evidenziazione dei profitti (area compresa tra la retta F e la retta CT)
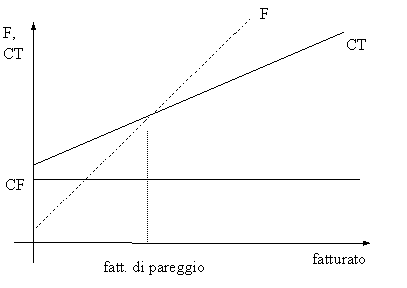
DETERMINAZIONE GRAFICA DEL FATTURATO DI PAREGGIO
(2) con evidenziazione dei margini di contribuzione (area compresa tra la retta F e la retta CV)
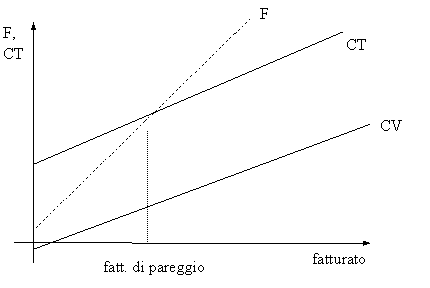
Può essere interessante, in molti casi, mettere a confronto le vendite previste (sulla base, ad esempio, delle risultanze di una ricerca di mercato) con le vendite che assicurerebbero all'impresa almeno il pareggio economico. Si ottiene così una misura del rischio intrinseco a queste previsioni, chiamata 'margine di sicurezza':
margine di sicurezza
Così, un margine di sicurezza di 0,30 sta ad indicare che le vendite possono essere fino al 30% inferiori rispetto al valore previsto senza che ciò comporti per l'impresa il conseguimento di una perdita.
Esiste una accezione 'finanziaria' del break-even, che viene calcolata considerando soltanto i costi cd. out-of-pocket, cioè quelli che comporteranno un esborso di denaro. Non rientrano in questa categoria le voci di ammortamento e di accantonamento ai fondi.
In pratica, queste analisi finanziarie risultano più efficaci, come vedremo nel capitolo ottavo, utilizzando le tecniche di financial planning.
Il BEP può infine essere espresso in relazione alla capacità produttiva (CP) dell'impresa. In tal caso esso assume il significato di load factor, cioè di fattore di 'sfruttamento' della capacità disponibile:
load factor 
b) Target di profitto
La domanda b) è sostanzialmente una variante della a): dato un obiettivo di profitto pari a U, per quale livello di produzione (e vendit 939d39j a) sarà possibile raggiungerlo?
Per rispondere è sufficiente inserire nella (1) il valore obiettivo di profitto U al numeratore e risolvere l'equazione per Q:
Q =
c) Il prezzo di equilibrio
Dato un livello produttivo pari a Q, per quale prezzo di vendita sarà possibile ottenere almeno un risultato economico non negativo?
In tal caso occorre esplicitare dalla (1) il prezzo (p) anziché la quantità (Q):
prezzo di equilibrio = cvu +
La (3) ci dice che il prezzo minimo praticabile da un'impresa che voglia conseguire almeno il pareggio economico è pari al costo medio di produzione, cioè alla somma del costo variabile unitario con il costo fisso unitario.
Al crescere delle quantità prodotte, riducendosi i costi medi, l'impresa potrà praticare prezzi più bassi. Questo fenomeno è noto con il nome di economie di volume produttivo.
La condizione (3) rappresenta una condizione di equilibrio per l'impresa nel medio-lungo termine. Nel breve termine, l'impresa può anche trovare conveniente praticare - temporaneamente - prezzi inferiori. Le ragioni sono molteplici, per esempio:
In tutti questi casi, il prezzo sarà accettabile dall'impresa se - secondo la logica marginalistica - apporta un beneficio netto all'impresa. Tale beneficio è costituito dal margine di contribuzione unitario (p - cvu), cui vanno tolte eventuali quote di costi fissi che - rispetto a quella vendita - rappresentano dei costi opportunità.
3. I LIMITI DEL MODELLO
Le ipotesi che stanno alla base dell'analisi di break-even sono alquanto riduttive e ne riducono il grado di realismo. Di seguito segnaliamo alcune delle limitazioni maggiori dell'analisi in questione:
4. L'ANALISI COSTI-VOLUMI-RISULTATI FATTA SUI BILANCI
Il bilancio ed in particolare il conto economico forniscono utili informazioni per comprendere i meccanismi di produzione del valore di un'impresa. In mancanza di informazioni più dettagliate, l'analisi costi-volumi-risultati può dunque essere condotta a partire dal bilancio, ma con opportuni accorgimenti. Manca infatti in questo documento - in linea generale - l'indicazione delle quantità prodotte e vendute dall'impresa così come la specificazione dei prezzi unitari e dei costi unitari. Vi è poi il problema delle variazioni di prodotti, che non consentono di identificare in modo agevole il costo della produzione venduta.
I passi da seguire per l'analisi di break-even sono i seguenti:
Fatturato di
pareggio = 
Suggeriamo di non considerare tra i costi fissi gli oneri finanziari poiché trattasi di costi che variano in relazione al livello di indebitamento, mentre rispetto alle quantità prodotte non sono né fissi né variabili. Le imposte sul reddito vanno escluse dall'analisi perché non sono costi. In definitiva, è conveniente riferire la condizione di pareggio economico al reddito operativo (EBIT nella versione anglosassone - earnings before interests and taxes). Tuttavia non è raro includere anche gli oneri finanziari tra i costi fissi, e riferire il pareggio economico al reddito prima delle imposte.
Esempio. L'impresa Alfa Spa - conti economici per gli anni 1996 e 1997
|
|
|
|
|
|
|
|
|
Ricavi di vendita |
|
|
|
(-) Costi operativi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Risultato operativo |
|
|
|
(-) Oneri finanziari |
|
|
|
Risultato ante-imposte |
|
|
|
Imposte sul reddito (50%) |
|
|
|
Risultato netto |
|
|
Dopo avere identificato i costi fissi ed i costi variabili, si determini il fatturato di pareggio dell'impresa Delta.
Soluzione.
Le voci di costo da consumi di materie prime a salari (inclusi) sono costi variabili. Sono costi fissi tutte le altre voci, eccetto le quote di accantonamento al fondo TFR che sono da considerarsi in parte fisse ed in parte variabili. Considereremo tra i costi fissi gli oneri finanziari.
CF = 52.900
CVT = 137.646
MCT = F - CVT = 189.000 - 137.646 = 51.356
Fatturato di
pareggio =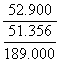 
= 194.682
Si tratta di un valore compreso tra il fatturato del 1996 e del 1997. Effettivamente, l'impresa ha conseguito una perdita nel 1997 e un utile nel 1996.
Si noti che l'impresa Delta ha un unico fatturato di pareggio. Il fatturato di pareggio indica infatti una condizione strutturale dell'impresa, definibile in funzione della sua 'struttura' di costi fissi e variabili e della sua redditività operativa. Se non mutano queste condizioni strutturali, non muta nemmeno il fatturato di pareggio (almeno in termini reali, cioè al netto di variazioni del livello dei prezzi-costo e dei prezzi-ricavo).
Se da un anno all'altro muta il suo grado di integrazione verticale, se migliorano i margini di contribuzione attraverso un contenimento dei costi di produzione, se aumenta il grado di differenziazione dei prodotti e quindi la misura del premium price, ecc. muterà anche la condizione strutturale di pareggio economico.
5. L'ANALISI DELLE LEVE
Se confrontiamo le equazioni del profitto (1) di diverse imprese, notiamo che queste non sono ugualmente sensibili alle variazioni nella quantità Q. In altri termini, ci sono imprese, pur appartenenti allo stesso settore di attività economica, il cui profitto si accresce fortemente in seguito ad un aumento nelle quantità, mentre ci sono altre imprese il cui profitto cresce meno che proporzionalmente. Tutto questo ha a che fare con il livello dei margini unitari di contribuzione: l'impresa con i più alti margini unitari beneficierà maggiormente di ogni aumento delle vendite. Si dirà allora che l'impresa ha un'elevata leva operativa.
La leva operativa è il parametro che misura l'elasticità dei profitti d'impresa alle variazioni dei volumi di produzione/vendita. Essa è misurata dal rapporto tra le variazioni incrementali del profitto e della quantità:
leva operativa =
e con opportune semplificazioni:
=
leva operativa =
Ad esempio, avere una leva operativa pari a 3 significa che una variazione del 10% (in + o in -) nelle vendite produce una variazione del 30% (nello stesso senso) nel profitto.
Oltre alla leva operativa (o dei volumi) è possibile calcolare anche la sensibilità del profitto a variazioni nei costi e a variazioni nei prezzi:
leva dei prezzi =
leva degli acquisti = 
Dall'analisi congiunta di questi parametri l'impresa è in grado di stabilire se sia più opportuno, sotto il profilo della convenienza economica, dar corso ad una strategia di aumento della quota di mercato (per sfruttare la leva operativa), di razionalizzazione interna (per sfruttare la leva dei costi) o di differenziazione competitiva (per ottenere un cd. premium price e sfruttare la leva dei prezzi).
Si noti che la leva dei prezzi è il reciproco del ROS (return on sales).
Esempio. Si consideri il seguente conto economico:
|
Fatturato |
|
|
Costi d'acquisto |
|
|
Margine di contribuzione |
|
|
Costi del personale (fissi) |
|
|
Ammortamenti |
|
|
Reddito operativo |
|
|
Oneri finanziari |
|
|
Reddito netto |
|
Le leve corrispondenti sono le seguenti:
|
|
Rispetto al reddito operativo |
Rispetto al reddito netto |
|
Leva dei prezzi |
|
|
|
Leva operativa |
|
|
|
Leva degli acquisti |
|
|
Per raddoppiare il reddito netto l'impresa potrà scegliere - rispettivamente - di:
aumentare i prezzi del 4%;
aumentare le vendite in quantità del 13,3%
ridurre i costi di acquisto del 5,7%
Il forte impatto sul reddito delle variazioni nei costi di acquisto è segnaletico dell'importanza di questa area gestionale nell'economia delle imprese (cfr. il capitolo sesto).
Esempio. Per un'impresa che intenda massimizzare il profitto, quale delle due opzioni seguenti sarà preferibile? (NB: assumiamo che la variazione delle vendite non influenzi in alcun modo il prezzo e che la variazione del prezzo non influenzi in alcun modo le vendite)
aumentare le vendite del 20%;
aumentare i prezzi del 20%;
entrambe le opzioni hanno lo stesso effetto sul profitto.
Soluzione. Essendo la leva dei prezzi sempre più elevata della leva operativa, la massimizzazione del profitto sarà, a parità di condizioni, sempre più agevole attraverso la manovra dei prezzi. In effetti, è sufficiente considerare che, per ottenere lo stesso incremento di fatturato, manovrando le quantità dovremo anche sostenere dei costi incrementali di produzione.
Specularmente, se l'obiettivo dell'impresa è quello, in una fase recessiva del mercato, di minimizzare le perdite, sarà più conveniente agire - a prescindere ovviamente da considerazioni di natura competitiva (necessità di conservare le quote di mercato) - sulle quantità prima che sui prezzi.
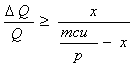
Spesso l'impresa subisce le variazioni del prezzo di
mercato ed è costretta a salvaguardare il risultato economico attraverso la
manovra delle quantità. In presenza di una caduta del prezzo di mercato,
l'aumento delle quantità dovrà essere almeno pari a:
dove x è la riduzione percentuale del prezzo imposta dal mercato.
In caso di aumento del prezzo di vendita, per mantenere invariato il risultato economico l'impresa dovrà evitare (a causa dell'elasticità della domanda ai prezzi) di subire una riduzione delle vendite (in quantità) superiore a:
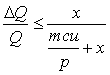
Dove x è l'aumento percentuale dei prezzi.
6. LA STRUTTURA DEI COSTI
Di significato simile alla leva operativa è l'elasticità dei costi totali alle variazioni di quantità. Essa ci indica di quanto variano (in %) i costi totali dell'impresa in conseguenza ad ogni variazione (%) nelle quantità prodotte. Si tratta quindi di una misura strettamente dipendente dalla natura dei costi dell'impresa, ed in particolare dalla maggiore o minore presenza di costi variabili.
elasticità dei costi =
=
=
elasticità dei costi =
L'elasticità dei costi assume valori compresi tra 0 (assenza di costi variabili) e 1 (assenza di costi fissi). Un valore pari a 0,80 significa che una variazione del 10% nei volumi produttivi comporta una variazione dell'8% nei costi totali.
Di significato equivalente è l'indice di elasticità dei costi misurato attraverso il rapporto tra costi variabili e costi fissi:
elasticità
dei costi = 
Esempio. I legami tra parametri. Consideriamo i seguenti valori per i parametri considerati:
leva dei prezzi = 25;
leva operativa = 10;
Quale sarà il corrispondente valore dell'elasticità dei costi?
Soluzione.
Fatto 100 il fatturato, data la leva dei prezzi, il profitto sarà pari a 4. Il MCT sarà allora pari a 40. I costi totali ammontano a 96, i costi variabili totali sono pari a 60 (F - MCT). Il grado di elasticità dei costi è quindi:
elasticità
dei costi =
= 0,625
Si consideri ora la seguente tabella, che rappresenta le previsioni di vendita per l'anno successivo e i dati di costo e ricavo di tre imprese appartenenti allo stesso settore di attività (i valori sono puramente indicativi):
|
|
impresa A |
impresa B |
impresa C |
|
prezzo |
|
|
|
|
costo variabile unitario |
|
|
|
|
margine unitario di contribuzione |
|
|
|
|
costi fissi |
|
|
|
|
vendite previste (unità) |
|
|
|
Le tre imprese producono lo stesso prodotto, che mettono in commercio allo stesso prezzo. Esse prevedono inoltre di collocare sul mercato lo stesso volume produttivo.
Diversa è invece la struttura produttiva che le tre imprese hanno posto in essere per poter operare: l'impresa C presenta un livello di costi fissi quattro volte più elevato dell'impresa A; i suoi costi variabili unitari di produzione sono invece sensibilmente inferiori a B e ad A. Ciò riflette la scelta di C di ricorrere il meno possibile a fornitori esterni.
Diverso è - in definitiva - il grado di integrazione verticale di queste imprese.
Un metodo per misurare il grado di integrazione verticale è il seguente:
Grado di integrazione verticale = 
dove VGP è il valore globale della produzione e VA è il valore aggiunto.
Una versione più approssimativa del parametro è la seguente:
Grado di integrazione verticale = 
=
Tornando alla tabella precedente, un confronto tra le tre imprese relativamente all'impatto del diverso grado di integrazione produttiva sulla loro struttura di costi può essere condotto utilizzando i parametri introdotti nel capitolo quarto:
|
|
impresa A |
impresa B |
impresa C |
|
profitto |
|
|
|
|
quantità di pareggio |
|
|
|
|
margine di sicurezza |
|
|
|
|
leva operativa |
|
|
|
|
elasticità dei costi |
|
|
|
Come si può osservare, le tre imprese prevedono di realizzare lo stesso profitto, ma presentano valori sensibilmente diversi nei parametri impiegati.
L'impresa A raggiungerà più presto il punto di pareggio, e potrà contare su un margine di sicurezza più elevato, il che la mette al riparo dalle conseguenze di possibili errori di previsione. In tal senso, essa è meno rischiosa delle altre due imprese. Per contro, è l'impresa C ad avere il valore di leva operativa più elevato. Essa potrà quindi beneficiare maggiormente di variazioni aumentative nelle vendite, anche se subirà i maggiori contraccolpi in caso di vendite inferiori alle previsioni. L'elasticità dei costi è massima per A, mentre C presenta una struttura di costi piuttosto 'rigida'.
In definitiva, A è la tipica impresa poco integrata, che cerca la massima flessibilità alle oscillazioni del mercato; C è invece la tradizionale impresa fortemente integrata, che ha uno spiccato orientamento alla crescita.
Un esempio di impresa con elevata leva operativa (del tipo C) è una società per l'esercizio della telefonia mobile. Il costo marginale di produzione del servizio di connettività è pressoché nullo. Elevatissimi sono invece gli investimenti (e quindi i costi fissi) nelle infrastrutture. Data la forte componente 'sunk' dei costi fissi, possiamo considerare l'intero fatturato realizzato come un flusso di cassa netto. Le stesse considerazioni possono essere fatte per una società concessionaria di autostrade.
STRUTTURE DI COSTO A CONFRONTO
quantità prodotta
7. IMPRESE MULTI-PRODOTTO E ANALISI COSTI/VOLUMI/RISULTATI
Il terreno ideale per l'applicazione dell'analisi costi/volumi/risultati è costituito dall'insieme delle imprese mono-prodotto e mono-business, quelle imprese, cioè, che realizzano un'unica produzione che collocano su un'unico mercato.
Anche in presenza di produzioni diversificate, l'analisi mantiene la sua efficacia se, all'interno dell'impresa, è possibile isolare nettamente le parti di essa (stabilimenti, reparti, linee produttive) nelle quali viene svolta la particolare produzione oggetto dell'analisi.
In realtà, molte imprese industriali, anche se non diversificate, realizzano produzioni congiunte, cioè producono le diverse varianti di uno stesso tipo di prodotto utilizzando le stesse linee produttive e, a volte, perfino le stesse macchine (cd. macchine flessibili). E' il caso dei produttori automobilistici o dei produttori di elettrodomestici, che offrono al mercato una ampia varietà di modelli diversi per colore, forma, prestazioni.
In questi casi, non avrebbe ovviamente molto senso calcolarsi il punto di pareggio per ogni variante di prodotto, per due ordini di ragioni:
Tuttavia, l'analisi sopra presentata può realizzarsi, pur perdendo parte della sua efficacia, con riferimento ad un 'prodotto medio', venduto ad un 'prezzo medio'.
Evidentemente, questo artificio non può essere accettato nel caso di imprese commerciali, come un supermercato od un grande magazzino. Non è infatti possibile parlare di prodotto medio quando l'assortimento offerto al pubblico comprende, ad esempio, prodotti per l'igiene personale, prodotti alimentari e articoli casalinghi.
In questi casi, ci soccorre il particolare meccanismo attraverso il quale queste imprese formano i prezzi di vendita. Si tratta del cd. metodo della percentuale di ricarico: il prezzo di vendita è cioè determinato 'caricando' sul costo di acquisto una determinata percentuale di questo costo. Ad esempio, se questa percentuale è pari al 30%, fatto 100 il costo di acquisto, il prezzo di vendita sarà pari a 130. La percentuale è ovviamente fissata in modo tale da consentire il recupero dei costi fissi e ottenere un congruo utile.
Si noti che per le imprese commerciali il costo variabile unitario corrisponde al costo di acquisto. Il prezzo di vendita può essere espresso nei termini seguenti:
prezzo = cvu (1 + x)
dove x è la percentuale di ricarico.
Se nella equazione del fatturato di pareggio sostituiamo il prezzo otteniamo:
fatturato di pareggio =
che è indipendente dal prezzo e dal costo di acquisto di un qualsiasi prodotto.
Esempio - L'impresa commerciale Alfa opera, con 10 punti di vendita, nel comparto della distribuzione de-specializzata. Essa intende aprire un nuovo punto di vendita al dettaglio. I costi fissi dell'operazione sono i seguenti:
-affitto locali: 30.000.000 annui;
-costi del personale: 150.000.000 annui;
-spese di acquisto delle attrezzature (scaffalature, mobili d'ufficio, registratori di cassa): 400.000.000; vita utile: 4 anni;
I costi variabili sono rappresentati dai costi di acquisto delle merci in assortimento. L'impresa definisce i prezzi con il metodo della percentuale di ricarico.
a) se la percentuale di ricarico viene fissata al 25%, quale fatturato annuo minimo garantirà il pareggio economico, cioè la copertura dei costi fissi e variabili?
b) le previsioni medie di vendita sono soggette ad una incertezza pari al 30% (in + o in -). Quale sarà, sulla base del fatturato di pareggio sopra determinato, il volume minimo previsto di vendita che dovrebbe garantire un'apertura senza rischi del punto di vendita?
c) l'impresa vuole ottenere dal nuovo punto di vendita un utile annuo di Lit. 300.000.000. Le previsioni di vendita sono di Lit. 2.000.000.000. Quale sarà la minima percentuale di ricarico praticabile?
d) a partire dai dati di cui al punto precedente, se l'impresa volesse incrementare gli utili annui del 30%, quale dovrebbe essere il necessario incremento del fatturato?
Soluzione
a) dalla equazione (6) otteniamo:
fatturato di pareggio =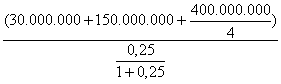 
= 1.400.000.000
b) a partire dalla formula del margine di sicurezza si ottiene:
margine di sicurezza =
fatturato minimo previsto =
c) si tenga presente che l'equazione del profitto per imprese che formano i prezzi col metodo della percentuale di ricarico è la seguente:
profitto = * Fatturato - CF
applicandola al caso in esame otteniamo:
x = 40,8%
d) calcoliamo ora la leva operativa:
leva operativa =
leva operativa =
quindi, per ottenere un aumento del 30% del profitto sarà necessario un incremento del fatturato del 15,5% circa (%), cioè pari a Lit. 310.000.000.
Esempio - L'impresa Gamma gestisce una catena di supermercati nel nord-est del Paese. I punti di vendita sono complessivamente 12. Il fatturato previsto per l'anno 1997 in ogni punto di vendita è pari a 2500 milioni di lire.
I costi fissi di ogni punto di vendita (spese per il personale, affitto locali) sono pari a 200 milioni di lire annui. I prezzi di vendita sono definiti, su tutti i prodotti e in tutti i supermercati, sulla base di una percentuale di ricarico del 25% sul costo di acquisto.
Tenendo conto che le spese generali (amministrazione, oneri finanziari, costi di struttura) che gravano complessivamente sull'impresa Gamma sono pari a 3 miliardi di lire, si determini:
a) l'utile netto previsto per il 1997;
b) il fatturato di break-even dei punti di vendita;
c) la percentuale di ricarico necessaria a realizzare un reddito operativo, a livello di punto di vendita, di Lit. 500.000.000.
Soluzione.
a) utile netto = * 2.500.000.000 * 12 - (200.000.000 * 12) - 3.000.000.000 = Lit. 600.000.000
b) fatturato di break-even = = Lit. 1.000.000.000
c) 500.000.000 = 2.500.000.000 * - 200.000.000
percentuale di ricarico = 39%
Conto economico e percentuale di ricarico.
La percentuale di ricarico praticata da un'impresa può anche essere desunta dal conto economico. Dalla:
Otteniamo:
e infine:
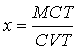
8. COSTI DI INVENDUTO VS. COSTI DI MANCATE VENDITE
Di fronte ad una domanda incerta e non perfettamente prevedibile, uno dei tipici dilemmi della gestione delle imprese consiste nella valutazione se sia preferibile correre il rischio di realizzare una produzione (o un volume di acquisti, se si tratta di un'impresa commerciale) eccedente la domanda effettiva o inferiore a quest'ultima. La questione si pone con particolare gravità in presenza di produzioni a forte deperibilità (come, ad esempio, molte produzioni alimentari) e/o elevato tasso di obsolescenza (come, ad esempio, l'abbigliamento di 'moda').
Nel caso di domanda superiore alla produzione (mancate vendite), l'impresa sopporta una perdita di margini di contribuzione pari al prodotto tra il margine unitario e la minor produzione realizzata. Nel caso invece di una domanda inferiore alla produzione, l'impresa consegue interamente i margini di contribuzione ma deve sopportare anche i costi della produzione eccedente.
Domanda eccedente la produzione = mancate vendite
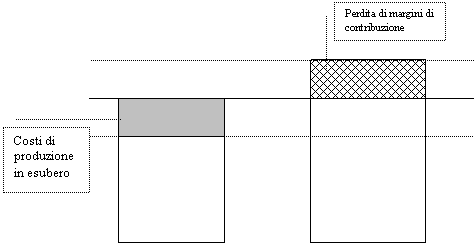
Costi variabili di produzione vs. margini unitari di contribuzione: è questo dunque il dilemma tra invenduto e mancate vendite. Imprese con alti margini e bassi costi variabili (come molte imprese di servizi: un albergo, un vettore aereo) preferiranno correre il rischio dell'invenduto. Viceversa, imprese con bassi margini e alti costi marginali (come le imprese commerciali o le imprese industriali a basso grado di integrazione verticale) preferiranno correre il rischio del sottoscorta.
Non bisogna però dimenticare che le mancate vendite hanno anche delle implicazioni sotto il profilo della customer satisfaction. La mancata disponibilità del prodotto abbassa il livello di servizio offerto con il pericolo di perdere il cliente a vantaggio dei concorrenti.
Diverso è invece il caso di mancata disponibilità (cd. sottoscorta) di materie prime e/o di semilavorati. In tali casi, l'eventuale blocco della produzione non comporta automaticamente una perdita di vendite, se l'impresa può contare su un adeguata disponibilità di prodotti finiti in magazzino.
Esempio.
Consideriamo una situazione decisionale di breve periodo, dove l'epoca 0 identifica il momento delle decisioni di produzione, mentre l'epoca 1 coincide con la vendita della produzione realizzata.
Com'è logico attendersi, le decisioni di produzione sono assunte sulla base delle previsioni di domanda. L'impresa sa di correre il rischio di "sbagliare" le previsioni, tuttavia - non potendo dar corso ad una produzione su commessa - deve stabilire in anticipo la quantità di produzione.
I dirigenti preposti alla previsione della domanda concordano su un livello "atteso" della stessa di 100 unità; essi sono però consapevoli - trattandosi di stime fortemente aleatorie - di correre il rischio che la domanda effettiva sia, all'epoca 1, anche sensibilmente diversa da quella stimata all'epoca 0. In particolare, l'impresa ritiene ugualmente probabile un errore per difetto e per eccesso fino ad un massimo del 20%.
La direzione commerciale fa presente che - al fine di garantire un adeguato servizio alla clientela - occorre assolutamente evitare il fenomeno delle "mancate vendite". Sarebbe quindi opportuno 'gonfiare' un po' la produzione per limitare questo rischio.
Dal canto loro, i responsabili della produzione sostengono che data l'elevata deperibilità del prodotto finito, sarebbe auspicabile evitare il fenomeno dell'"invenduto". L'impresa si troverebbe altrimenti ad aver sostenuto dei costi di produzione non più recuperabili con i prezzi di vendita.
Chi ha ragione?
Soluzione.
Cerchiamo innanzitutto di quantificare i massimi costi di "invenduto" e di "mancate vendite" nel caso specifico.
Se la domanda effettiva è pari a 120 unità, l'impresa - avendo limitato la sua produzione a 100 unità - conseguirà un profitto pari a:
profitto = 100 * (p - cvp) - CF
Se la produzione fosse stata di 120 unità, il profitto dell'impresa sarebbe stato pari a:
= 120 * (p - cvp) - CF
Il costo delle "mancate vendite" è dunque pari a:
(a) costo delle mancate vendite = 20 * (p - cvp) = 20 * mcu
Se invece la domanda effettiva è pari a 80 unità l'impresa conseguirà un profitto di:
profitto = 80 * p - 100 * cvp - CF
Se la stima iniziale fosse stata corretta, il profitto conseguito sarebbe stato superiore:
= 80 * (p - cvp) - CF
La differenza tra il profitto conseguito e quello massimo conseguibile, dato quel livello di domanda, sarà quindi pari a:
(b) costo dell'invenduto = 20 * cvp
La chiave del problema sta dunque nel confronto tra margine di contribuzione unitario (mcu) e costi variabili unitari di produzione (cvp). Se i margini sono superiori ai costi di produzione allora le mancate vendite peseranno più dell'invenduto. Se i margini sono inferiori ai costi, invece, sarà opportuno evitare l'invenduto.
In definitiva, se il rapporto mcu/p è maggiore di 0,5 avranno ragione gli uomini della direzione commerciale a chiedere di 'gonfiare' un po' la produzione. Se invece il rapporto è inferiore a 0,5 sarà meglio seguire le indicazioni della direzione di produzione e limitare la produzione (o gli acquisti, se si tratta di un'impresa commerciale).
Una produzione eccedente la domanda non si trasforma automaticamente in un costo di invenduto. Se il prodotto è immagazzinabile, l'impresa potrà conservare la produzione eccedente e 'smaltirla' gradualmente, incorrendo in un semplice costo di immobilizzo di capitale nelle scorte:
Costo unitario di immobilizzo = costo del prodotto a scorta (cvp) x costo di mantenimento % (i) x tempo necessario per la vendita
Sovente però il prodotto eccedente che viene messo a scorta per la successiva rivendita viene a perdere progressivamente il suo valore, per effetto dell'obsolescenza. E' il caso, ad esempio, di prodotti a forte contenuto tecnologico, come i personal computer, o di prodotti a forte componente 'moda', come l'abbigliamento. In tal caso, l'impresa dovrà velocizzare il tempo di vendita attraverso vendite promozionali o altre forme di sconto sui prezzi. Il costo dell'obsolescenza sarà così determinato:
Costo di obsolescenza = cvp + costo unitario di immobilizzo - prezzo residuo di realizzo
9. ESERCIZI SVOLTI
Esercizio 1 - L'impresa Alfa opera nel settore dell'elettronica di consumo. Uno dei suoi 5 stabilimenti è dedicato alla produzione di radiosveglie. Ciascuna unità prodotta è venduta per $66; i costi fissi a livello di stabilimento comprendono gli ammortamenti degli impianti e dei macchinari, le spese di manutenzione ordinaria, il costo del personale direttivo e di quello addetto alla supervisione, i canoni di leasing e l'affitto di alcuni capannoni. Per una produzione fino a 200.000 unità annue i costi fissi annui ammontano a $1.950.000. I costi variabili di produzione (costi della manodopera diretta, costi di energia, consumi di materie prime e di componenti) sono pari a $20 per unità, cui si aggiungono $7 di spese di vendita (provvigioni alla rete di vendita).
a) qual è il profitto o la perdita annua dell'azienda in corrispondenza a 40.000 unità vendute?
b) qual è il punto di pareggio?
c) qual è il grado di leva operativa a 40.000 e a 60.000 unità?
d) che cosa accade al punto di pareggio se il prezzo di vendita sale a 78 $?
e) che cosa accade al punto di pareggio se il prezzo di vendita sale a 78 $, ma i costi variabili salgono a 39$ l'unità?
Soluzione:
a) dalla equazione del profitto (1) otteniamo:
profitto (perdita) = $(66 - 27) * 40.000 - $1.950.000 = ($390.000)
b) dalla (2) otteniamo:
Q = 
= 50.000
c) dalla (4) si ottiene:
leva operativa = = valore negativo (non significativo)
leva operativa = 
= 6
d) dalla (2) si ottiene:
Q = 
= 38.240
e) sempre dalla (2) otteniamo:
Q = 
= 50.000
Esercizio 2 - L'impresa Gamma opera nel settore degli alimenti per l'infanzia. Essa sta valutando l'opportunità di lanciare un nuovo prodotto per la prima colazione. Il ciclo di vita del nuovo prodotto è stimato in 5 anni. Le spese di ricerca e sviluppo, già appositamente sostenute, ammontano a $500.000. Per la produzione l'impresa potrebbe utilizzare i macchinari già in sua dotazione, che attualmente sono parzialmente inutilizzati, per mancanza di impieghi alternativi. La quota di costi fissi imputabile è stimata in $1.200.000 annui. La vendita del nuovo prodotto sarebbe invece assicurata attraverso il potenziamento della rete di vendita dell'impresa, per un costo fisso incrementale di $300.000 annui. I costi variabili di produzione e commercializzazione sono pari a $50 per unità. La quantità che ci si attende di produrre e vendere è di 70.000 unità annue. Il prezzo di vendita prevedibile, tenuto conto del prezzo dei prodotti concorrenti, è di $70.
a) E' conveniente il lancio del nuovo prodotto?
b) Quale può considerarsi la quantità di pareggio per l'impresa?
Soluzione:
a) Per valutare la convenienza economica del lancio del nuovo prodotto è necessario isolare in modo preciso gli effetti economici (costi e ricavi) che si produrranno a partire dal lancio da quegli effetti economici che si realizzerebbero comunque o che si sono già realizzati. Si tratta cioè di applicare la logica incrementale. Sotto tale profilo, i costi fissi di produzione non rappresentano un costo incrementale, poiché l'impresa li sosterrebbe comunque. Né questi costi rappresentano un costo opportunità, poiché non sembrano esserci, allo stato attuale, altre forme di sfruttamento della capacità produttiva inutilizzata. Per quanto concerne invece le spese di ricerca e sviluppo, esse sono già state sostenute, quindi la scelta se lanciare o meno il nuovo prodotto non ne può più modificare l'entità. Gli unici costi che appaiono effettivamente 'incrementali' sono i costi fissi di vendita e i costi variabili di produzione.
Applicando la (1) otteniamo quindi:
profitto 'incrementale' = $(70 - 50) * 70.000 - $300.000 = $1.100.000
che è un risultato abbondantemente positivo.
Si noti che se avessimo imputato anche i costi non incrementali avremmo ottenuto un risultato nettamente sfavorevole al lancio:
perdita 'imputabile' = $(70 - 50) * 70.000 - $(300.000 + 1.200.000 +
b) I ragionamenti appena condotti non escludono che, una volta deciso il lancio del nuovo prodotto, l'impresa possa voler recuperare tutti i costi 'imputabili' all'operazione, anche se non incrementali. Nel nostro caso, sarà possibile 'azzerare' la perdita sopra evidenziata attraverso un aumento del prezzo o delle quantità vendute:
Quantità di pareggio =
Prezzo di equilibrio = cvu + = $73 circa
Commento
L'esempio si rivela particolarmente indicato, oltre che a presentare un'applicazione di analisi costi-volumi-risultati, ad introdurre il tema delle valutazioni economiche (cfr. il capitolo successivo).
Soltanto i costi che hanno natura incrementale (che conseguono cioè dalla decisione) possono essere considerati nel 'bilancio' della decisione. Non hanno questa natura i costi di R&S ( si tratta di sunk cost) e i costi in capacità produttiva inutilizzata (si tratta di costi non incrementali, poiché si dovrebbero comunque sostenere, anche in ipotesi di non lancio del nuovo prodotto).
Come si può notare, vi sono dei costi tipicamente fissi (quelli da sostenere per il potenziamento della rete di vendita) che nella valutazione di questa decisione sono considerati costi incrementali. Il criterio di 'fissità' dei costi fa infatti riferimento al loro comportamento di fronte a variazioni dei livelli di produzione/vendita. Ai fini decisionali, invece, un costo è incrementale o non incrementale. Ci possono essere costi fissi incrementali così come costi variabili non incrementali (come i costi di produzione degli altri prodotti dell'impresa in questione).
La convenienza economica di una decisione non è una caratteristica intrinseca ad essa ma muta in funzione del momento storico in cui viene valutata: ad esempio, prima dell'investimento in R&S la convenienza del lancio è minore di quella valutata dopo l'investimento, poiché il costo relativo è diventato 'affondato' e quindi, per definizione, non incrementale.
La convenienza economica di una decisione muta inoltre in funzione del contesto. Se l'impresa non avesse già avuto a disposizione dei macchinari privi di costo opportunità avrebbe dovuto procurarseli, 'caricando' sulla decisione il relativo costo.
Esercizio 3 - L'impresa Beta opera come sub-fornitore certificato di un grande produttore automobilistico, a cui vende sedili per auto. I rapporti con il committente sono regolati da contratti annuali cd. 'aperti', che cioè non specificano preventivamente le quantità. Tuttavia, il sub-fornitore ritiene di poter ragionevolmente attendersi dall'acquirente richieste per 60 mila unità per il presente esercizio. Tenuto conto dell'incertezza che grava su queste previsioni, e volendo ridurre il più possibile i rischi, l'impresa Beta vuole garantirsi un margine di sicurezza del 25%.
I costi fissi industriali e le spese generali ammontano a Lit. 3 miliardi, mentre i costi variabili industriali unitari ammontano a Lit. 150.000. L'impresa non sostiene altri costi.
a) a quale prezzo di vendita dovrà offrire al committente la propria produzione?
b) quale sarà il livello di profitto realizzato in corrispondenza del livello previsto di vendite (60 mila unità)? e la leva operativa?
c) di quanto dovranno aumentare le vendite (in %), rispetto al livello previsto, perché il profitto cresca di una percentuale pari al 10%?
Soluzione:
a) Per avere un margine di sicurezza del 25% l'impresa deve realizzare il break-even ad un livello di vendite pari al 25% in meno di quelle previste, cioè ad un livello di 45.000 unità. In corrispondenza a questo volume di vendite, il prezzo minimo compatibile col pareggio economico sarà:
prezzo minimo = 150.000 +
b) dall'equazione del profitto:
profitto = (216.667 - 150.000) * 60.000 - 3.000.000.000 = 1.000.000.000
leva operativa =
c) Con una leva operativa pari a 4, sarà sufficiente un aumento del 2,5% delle vendite per ottenere una crescita del 10% del profitto.
Esercizio 4 - L'impresa Beta produce circuiti stampati. Essa è fornitore esclusivo, di tipo OEM (Original Equipment Manufacturing), di un importante produttore di apparecchiature per il videonoleggio. I suoi costi fissi annui ammontano a $1.000.000. I costi variabili unitari ammontano a $20. Il fabbisogno previsto dell'acquirente è pari a 15.000 unità. Se l'impresa vuole assicurarsi un margine di sicurezza del 50%, a quale prezzo dovrà vendere i propri prodotti? Quale sarà il livello di leva operativa in corrispondenza alla domanda prevista?
Soluzione.
Avere un margine di sicurezza del 50% significa avere un BEP pari a:
vendite previste - margine di sicurezza (50%) = 15.000 - (0,50 * 15.000) = 7.500
prezzo minimo = cvu +
leva operativa = mcu *
10. ESERCIZI DA SVOLGERE
1. Con riferimento alle due seguenti imprese:
|
|
impresa A |
impresa B |
|
prezzo |
|
|
|
costo variabile unitario |
|
|
|
costi fissi |
|
|
|
unità vendute |
|
|
Si indichi quale di esse presenta il livello più elevato dei seguenti parametri:
|
(barrare la casella corretta) |
A |
B |
uguale |
|
leva operativa |
|
|
|
|
elasticità dei costi |
|
|
|
|
break-even point |
|
|
|
|
risultato economico |
|
|
|
|
leva dei prezzi |
|
|
|
|
margine di sicurezza |
|
|
|
|
leva degli acquisti |
|
|
|
|
margine unitario di contribuzione |
|
|
|
|
costi medi unitari |
|
|
|
|
fatturato |
|
|
|
2. Un'impresa del settore della sedia - fortemente integrata verticalmente - intende avviare un rapporto di fornitura con la Verniciatura Sole Srl, chiudendo il reparto di verniciatura interno. Qual è l'impatto di una simile decisione su:
|
(barrare la casella corretta) |
cresce |
nessun impatto |
si riduce |
impatto incerto |
|
break-even point |
|
|
|
|
|
elasticità dei costi |
|
|
|
|
|
fatturato |
|
|
|
|
|
fatturato di pareggio |
|
|
|
|
|
grado di integrazione verticale |
|
|
|
|
|
leva degli acquisti |
|
|
|
|
|
leva dei prezzi |
|
|
|
|
|
leva operativa |
|
|
|
|
|
livello dei costi fissi |
|
|
|
|
|
margine di sicurezza |
|
|
|
|
|
margine unitario di contribuzione |
|
|
|
|
|
mcu/p |
|
|
|
|
|
quota di mercato |
|
|
|
|
3. Stabilire la verità/falsità delle seguenti proposizioni:
|
|
Vero |
Falso |
|
La leva operativa cresce al crescere dell'elasticità dei costi ai volumi produttivi |
|
|
|
La leva dei prezzi può essere inferiore alla leva operativa |
|
|
|
Il ricorso ai fornitori può ridurre l'elasticità dei costi |
|
|
|
Il ricorso all'opzione buy può aumentare il punto di pareggio |
|
|
|
A parità di margine di sicurezza, di leva operativa, di quantità vendute, di costi fissi, due imprese hanno lo stesso profitto |
|
|
|
Più alto il rapporto mcu/p più alto il grado di integrazione verticale |
|
|
|
Più basso il rapporto mcu/p maggiore la leva operativa |
|
|
|
Le decisioni make/buy sono ininfluenti sui costi dell'impresa |
|
|
|
La leva operativa e la leva degli acquisti crescono assieme |
|
|
|
La leva degli acquisti non può essere superiore alla leva operativa |
|
|
|
Due imprese con lo stesso margine di sicurezza hanno lo stesso profitto |
|
|
|
Le economie di volume sono la conseguenza degli aumenti di capacità produttiva |
|
|
|
Le economie di apprendimento aumentano al crescere della produzione cumulata |
|
|
|
Le economie di volume non dipendono dal grado di integrazione verticale |
|
|
4. A fronte di una previsione di vendite di 60 mila unità per il presente esercizio, l'impresa Beta vuole garantirsi un margine di sicurezza del 25%. I costi fissi industriali e le spese generali ammontano a 3 miliardi, mentre i costi variabili industriali-commerciali unitari ammontano a Lit. 150.000. L'impresa non sostiene altri costi.
A quale prezzo di vendita dovrà collocare sul mercato la propria produzione?
Quale sarà il livello di profitto realizzato in corrispondenza del livello previsto di vendite (60 mila unità)? E la leva operativa?
Di quanto dovranno aumentare le vendite (in %), rispetto al livello previsto, perché il profitto cresca di una percentuale pari al 10%?
5. L'impresa Beta sostiene annualmente costi fissi per $1.000.000. I costi variabili unitari ammontano a $20. La domanda prevista è pari a 15.000 unità. Se l'impresa vuole assicurarsi un margine di sicurezza del 50%, a quale prezzo dovrà vendere i propri prodotti? Quale sarà il livello di leva operativa in corrispondenza alla domanda prevista?
6. L'impresa Gamma sta valutando l'opportunità di lanciare un nuovo prodotto. I costi fissi su base annua sono stimati pari a 12.000 $. I costi variabili sono pari a 50 $ per unità. La quantità che ci si attende di produrre e vendere è di 700 unità annue. In corrispondenza di quale prezzo una quantità di 700 unità rappresenta il punto di pareggio?
7. L'impresa Alfa sostiene costi fissi per Lit. 30.000.000 annui. L'impresa definisce i prezzi con il metodo della percentuale di ricarico (33,3 % sui costi variabili unitari). L'impresa si è prefissata un obiettivo di profitto di Lit. 20.000.000.
8. L'impresa Beta sostiene costi fissi per Lit. 15.000.000 annui. L'impresa definisce i prezzi con il metodo cd. della percentuale di ricarico (33,3% sui costi variabili unitari).
a) Per quale livello di fatturato sarà realizzato il pareggio economico?
b) Sulla base dei dati di cui sopra, per quale livello di fatturato sarà possibile raggiungere un obiettivo di profitto di Lit. 10.000.000?
c) Si calcolino gli indici di leva operativa e di elasticità dei costi in corrispondenza al livello di fatturato di cui al punto b).
9. L'impresa Delta presenta, in corrispondenza dell'attuale livello di prezzo (600 per unità), un grado di leva operativa pari a 5. L'impresa definisce i prezzi col metodo della percentuale di ricarico. Tale percentuale è pari al 50%. I costi fissi ammontano a lire 10.000.000. Si determini la quantità prodotta/venduta e il reddito corrispondente.
10. L'impresa Alfa sostiene costi fissi per lire 20.000.000 annue. La quantità prodotta e venduta è pari a 10.000 unità. Il prezzo è determinato col metodo della percentuale di ricarico sui costi variabili unitari; tale percentuale è fissata al 33,3%. Quale prezzo di vendita deve fissare se vuole garantirsi un margine di sicurezza del 25%? Si calcoli altresì la leva operativa e l'elasticità dei costi in corrispondenza al livello di vendite previste.
11. L'impresa commerciale Alfa pratica dei prezzi di vendita col metodo della percentuale di ricarico sui costi d'acquisto. I suoi costi fissi ammontano a $100.000; il fatturato di break-even è pari a $1.000.000. Si determini la percentuale di ricarico.
12. L'impresa Delta realizza il break-even per un fatturato pari a lire 1.000.000.000. I prezzi sono determinati con il metodo della percentuale di ricarico sui costi variabili (tale percentuale è fissata al 50%). Qual è il grado di leva operativa in corrispondenza di un fatturato pari a 1.200.000.000?
13. Per un'impresa che intenda minimizzare le perdite, quale delle due opzioni seguenti sarà preferibile?
|
diminuire le quantità vendute del 2%, a parità di prezzo |
|
|
diminuire i prezzi del 2%, a parità di quantità vendute |
|
|
entrambe le opzioni hanno lo stesso effetto sul profitto |
|
14. Per un'impresa che intenda minimizzare le perdite, quale delle due opzioni seguenti sarà preferibile? Si tenga presente che, nel caso considerato, la leva dei prezzi è pari a 25; la leva operativa è pari a 10; la leva degli acquisti è pari a 12.
|
diminuire le quantità vendute del 5%, a parità di prezzo |
|
|
diminuire i prezzi del 2%, a parità di quantità vendute |
|
|
entrambe le opzioni hanno lo stesso effetto sul profitto |
|
Può trattarsi, a seconda del settore industriale, di automobili, frigoriferi, capi di abbigliamento, circuiti elettronici, ecc.
Si pensi, ad esempio, ai costi del personale, ai canoni di locazione dei capannoni, alle rate di rimborso dei prestiti.
Rientrano in questa categoria i costi delle materie prime, i costi dei semilavorati e dei componenti impiegati per realizzare il prodotto finito, i costi delle lavorazioni esterne, i costi della manodopera diretta, i costi dell'energia, ecc.
Per un esempio di ragionamento marginalistico nella definizione del prezzo nei rapporti tra acquirenti e fornitori, cfr. il seguito
Si potrebbe osservare che in entrambi i casi (invenduto o sottoscorta) l'impresa subisce una perdita di margini di contribuzione:
avendo fatto affidamento 'a priori' su questi margini, se la produzione resta poi invenduta;
avendo riscontrato questa perdita soltanto 'a posteriori', nel caso di domanda superiore alle attese (mancate vendite).
Ma, pur quantitativamente identica, si tratta di una perdita 'qualitativamente' diversa:
i margini persi con l'invenduto sono margini su cui erroneamente l'impresa aveva conto (a causa degli errori di previsione); sono margini che - alla prova dei fatti - non erano ottenibili e sui quali non ha senso avere rimpianti;
i margini persi con le mancate vendite sono invece margini 'persi' effettivamente, se non altro perché sono stati probabilmente guadagnati da un concorrente.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024
