Elementi di Matematica Finanziaria - CAPITALIZZAZIONE SEMPLICE

Si indica con t il tempo di impiego del capitale, vale a dire il tempo trascorso il quale il creditore o mutuante riceve in restituzione la somma prestata e il compenso dovuto.

Quindi I e C sono lettere che denotano somme di denaro, mentre t indica un intervallo di tempo(generalmente espresso in anni 515c26f , o mesi , o giorni).

L'interesse è direttamente proporzionale tanto al capitale quanto al tempo di impiego.

La legge dell'interesse semplice è la seguente:

I=C*i*t

Il tasso si esprime usualmente in percentuale: anziché dire, ad esempio, che si ha un tasso dello 0,07 annuo, si dice che si ha un tasso del 7%(infatti: 0,07=7/100).

Il tasso è sempre riferito ad un periodo di tempo, generalmente l'anno.

Il tempo t di impiego del capitale deve essere misurato rispetto alla stessa unità di tempo a cui è riferito il tasso, e cioè in anni se il tasso è annuo, in semestri se il tasso è semestrale, e così via.

Rappresentazione grafica dell'interesse semplice:

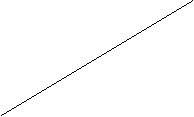
I I=C*i*t

0 t

Se ho due tassi ,ovvero i1 e i2 e so che i1<i2 allora graficamente avrò:

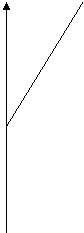
I I=C*i2*t

I=C*i1*t

0 t

Esempio:

Calcolare a quanto ammonta l'interesse sul capitale di un milione , dopo 9 mesi, se il tasso è del :

a)   

b)    5% semestrale

c) 1,25% mensile.

Soluzione:

a)

C=1000.000; t=9/12(=3/4); i=0,07

Da notare che il tasso è annuo dunque anche il tempo deve essere espresso in anni ovvero 9 mesi sono 9 dodicesimi di anno e in un anno vi sono 12 mesi dunque 9/12.

Da cui: I=C*i*t I=1.000.000*0,07*9/12=52.500

b)

C=1000.000; t=9/6; i=0,05

Da notare che il tasso è semestrale dunque anche il tempo deve essere espresso in semestri e in un anno vi sono 2 semestri dunque 12 mesi diviso 2 semestri significa 6(oppure più semplicemente un semestre è formato da 6 mesi), quindi 9 mesi sono equivalenti a 9 mesi su 6 mesi ovvero su un semestre.

Da cui: I=C*i*t I=1.000.000*0,05*9/6=75.000

c)

C=1000.000; t=9/1; i=0,0125

Da notare che il tasso è mensile e in un anno vi sono 12 mesi dunque 12 mesi diviso i mesi che vi sono in un anno e si ottiene 1 che non è altro che il denominatore della frazione che indica il tempo.

Da cui:I=C*i*t I=1.000.000*0,0125*9=112.500

FORMULE INVERSE:

La nostra formula di capitalizzazione semplice e diretta è la seguente:

I=C*i*t

Quindi si hanno quattro grandezze economiche che sono l'interesse, il capitale, il tasso di interesse e infine il tempo di impiego del capitale.

Conoscendo almeno tre di queste quattro grandezze sono in grado di determinare la grandezza mancante:

quindi se sono dati:

a)    I,i,t posso determinare C che è uguale a : C=I/(i*t)

b)    I,C,i posso determinare t che è uguale a: t=I/(C*i)

c) I,C,t posso determinare i che è uguale a: i=I/(C*t)

Esempio:

i dati sono i seguenti:

C=1.000.000; t=9/12; i=0,08; I=60.000

I=C*i*t I=1.000.000*9/12*0,08= 60.000

C=I/(i*t) C= 60.000/(0,08*9/12)=60.000/0,06=1.000.000

T= I/(C*i)=60.000/(1.000.000*0,08)=60.000/80.000=0,75anni devo moltiplicare 0,75 per i giorni che vi sono in un anno(analogamente se avessi un tasso semestrale dovrei moltiplicare il risultato per i giorni che vi sono in un semestre) 0,75*365=274 giorni circa.

I=(tasso)=I/(C*t)=60.000/(1.000.000*9/12)=60.000/750.000=0,08 se voglio trasformare il tasso in percentuale devo solo moltiplicare per 100

Il MONTANTE , si indica con M, ed è  dato dalla somma del capitale e dell'interesse.

Dunque il montante si può esprimere nel seguente modo:

M=C+I

Abbiamo visto che l'interesse I si trova con la seguente formula:

I=C*i*t

Allora il montante si può scrivere come:

M=C+C*i*t

Mettendo in evidenza il capitale allora si giunge alla formula corretta della capitalizzazione semplice ovvero:

M=C*(1+i*t)

RAPPRESENTAZIONE GRAFICA DEL MONTANTE:

è da notare che a differenza dell'interesse la nostra retta non parte dall'origine degli assi e questo perché nel calcolo del montante si addiziona l'interesse, che è variabile è che dipende sia dal tempo di impiego del capitale sia dal tasso d'interesse, a qualcosa di fisso che è rappresentato dal nostro capitale.

Quindi , dal punto di vista analitico l'intersezione della retta con le ordinate non è altro che il nostro capitale di partenza.

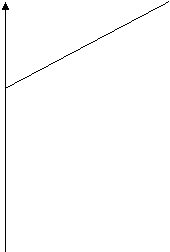
M M=C*(1+i*t)

C

0 t

Esempio:

Si impiegano L. 927.000 al tasso del 10,25% per 8 mesi.

Si determini il montante.

N.B.: quando nulla viene detto il tasso d'interesse si intende in anni, dunque non vi è nessuna manipolazione da fare relativamente al tempo.

Da ricordare in ogni caso che sempre tasso d'interesse e tempo viaggiano parallelamente.

C=927.000

I(tasso)=10,25/100=0,1025

T=8/12

M=C*(1+i*t)

M=927.000*(1+0,1025*8/12)

M=927.000*(1+0,0683333333)

M=927.000*(1,0683333333)

M=990.345

FORMULE INVERSE:

data la formula del montante ovvero:

M=C*(1+i*t)

Posso determinare:

I= M-C

A questo punto , determinato I ovvero l'interesse, so che lo stesso si determina con la formula seguente:

I=C*i*t

Dunque le formule inverse, per determinare il tempo, il tasso d'interesse, il capitale, sono identiche a quelle viste in precedenza.

INTERESSE ANTICIPATO E POSTICIPATO:

Quando una persona affida un incarico ad un'altra offrendole una ricompensa, può darla prima che quest'ultima abbia svolto l'incarico oppure dopo che la richiesta sia stata soddisfatta.

Nel primo caso si dice che il compenso è anticipato, nel secondo che è posticipato.

In genere l'interesse è posticipato: ad esempio se presto 1.000 al 7% per un anno, trascorso l'anno ricevo 1.000  più l'interesse.

In alcuni casi, tuttavia, l'interesse  viene anticipato.

Se ad esempio , presto 1000 come nel caso precedente, posso ricevere subito 70 di interesse. Cioè in pratica, do al debitore solo 930, passato un anno, egli mi darà 1000.

A parità di tasso l'interesse posticipato conviene al debitore, quello anticipato al creditore.

In generale il creditore preferirà avere un interesse anticipato in modo da poter usufruire della differenza tra quanto dovuto e quanto effettivamente dato per investimenti più redditizi , mentre il debitore è più favorevole a corrispondere un interesse posticipato in quanto otterrà un maggiore quantitativo di denaro subito e non dovrà preoccuparsi della restituzione del denaro più l'interesse fino alla scadenza.

Esempio:

un BOT annuo è offerto a L.89 per ogni L.100 di valore nominale.

Qual è il suo rendimento?

Soluzione:

affermare che il BOT è offerto a L.89 per ogni L.100 di valore nominale significa che il risparmiatore presta allo Stato, ad esempio, L.8.900.000 e riceve , dopo un anno, L.10.000.000.

si può dire che il BOT rende l'11% anticipato: il risparmiatore presta L.100, riceve subito L.11 d'interesse(per cui versa L.89) e, alla scadenza, gli vengono restituite L.100.

dalla legge sull'interesse ovvero:

I=C*i*t

Allora abbiamo che :

11=89*i*1

da cui ricaviamo il tasso d'interesse come i=I/(C*t) i=11/(89*1) i=11/89=0,1236

quindi sappiamo che dal punto di vista del creditore egli otterrà l'11% anticipato oppure il 12,36% posticipato: sembrerebbe convenire l'interesse posticipato, ma potrebbero esservi delle forme di investimento più redditizie per il creditore  che facciano in modo che la differenza 12,36%-11%=1,36% espressa sotto forma di capitale versato in difetto alla sottoscrizione dei BOT sia più redditizia ad esempio grazie alla sottoscrizione di azioni o obbligazioni o altri titoli di Stato o quote di fondi comuni, etc...

CAPITALIZZAZIONE COMPOSTA:

Si dice periodo di capitalizzazione l'intervallo di tempo trascorso il quale l'interesse viene aggiunto al capitale e diventa fruttifero(cioè produce a sua volta un interesse).

Supponendo il tempo di impiego =1 la legge sul montante vista in precedenza ovvero:

M=C*(1+i*t)

Diviene la seguente:

M=C*(1+i*1)

M=C*(1+i)

quest'ultima formula ci dice a quanto ammonta il capitale più gli interesse dopo 1 anno(t=1) dunque per avere una formula generalizzata sulla capitalizzazione composta basta aggiungere la variabile anni.

Così la formula per la determinazione del montante in regime di capitalizzazione composta risulta essere:

M=C*(1+i)^t

Dove t deve essere un numero intero positivo ovvero deve appartenere a Z+, e dove t rappresenta i periodi di capitalizzazione(più periodi allora si parla di capitalizzazione composta: capitalizzazione composta ci si riferisce ad un impiego o investimento a m/l termine e non a breve termine, come per la capitalizzazione semplice).

Esempio:

calcolare il montante di L. 100.000.000 impiegate ad interesse composto al tasso del 7% per 5 anni.

Allora i dati che ho sono:

C=100.000.000

I=(tasso)=7/100=0,07(annuo)

T=5 anni

Allora applicando la seguente:

M=C*(1+i)^t

M=100.000.000*(1+0,07)^5

M=100.000.000*(1,07)^5

M=100.000.000*(1,402551731)

M=140.255.173

Esempio:

calcolare il montante di L.1000 impiegate per 5 anni al 2,3% trimestrale con capitalizzazione trimestrale.

I dati che ho sono:

C=1.000

I=(tasso)=0,023 trimestrale

T=(in trimestri)=20(in 5 anni vi sono 20 trimestri)

M=C*(1+i)^t

M=1.000*(1,023)^20

M=1.576

Esempio:

calcolare il montante di L. 1.000 impiegate allo 0,9% mensile, con capitalizzazione mensile, per 100 anni:

i dati che ho sono:

C=1.000

I(tasso)=0,009 mensile

T=100 anni

In 100 anni vi sono 1200 mesi dunque:

M=1.000*(1,009)^1200

M=46.708.883

Nel caso in cui si abbia un tempo di capitalizzazione non intero ovvero non appartenente a Z+ bensì appartenente a Q+ ovvero numeri razionali positivi la legge della capitalizzazione composta passa da:

M=C*(1+i)^t

A:

M=C*(1+i)^t*(1+i*f)

Esempio:

Calcolare il montante di L. 1.700.000 impiegate al 9% per un periodo di 5 anni e 4 mesi.

I dati che abbiamo sono:

C=1.700.000

I=(tasso)=0,09 annuo

T=5 anni e 4 mesi: quindi 5 numero intero positivo(ovvero nella formula è t) e 4 numero, riferito all'anno(in quanto il tasso è annuo) diviene 4/12 dunque numero razionale positivo(nella formula è f).

Allora:

M=C*(1+i)^t*(1+i*f)

M=1.700.000*(1+0,09)^5*(1+0,09*4/12)

M=1.700.000*(1,538623955)*(1+0,03)

M=1.700.000*(1,538623955)*(1,03)

M=1.700.000*(1,584782674)

M=2.694.130

In generale , grazie all'uso delle tavole finanziarie si possono affrontare i problemi inversi che genera la capitalizzazione composta ovvero la determinazione di:

tasso d'interesse;

tempo d'impiego del capitale;

determinazione del capitale.

Partendo dalla formula della capitalizzazione composta ovvero:

M=C*(1+i)^t

Determino:

1)il tasso come:

(1+i)^t=M/C

1+i= sr(tempo)M/C

i=sr(tempo)M/C -1

2)il tempo come:

t=(logM - Log C)/Log(1+i)

3)il capitale come:

C= M/(1+i)^t

C=M*(1+i)^-t

LO SCONTO COMMERCIALE:

Dire somma scontata S o valore attuale V è equivalente in generale.

Si dice sconto e si indica con S la differenza tra C e V.

S=C-V

Per determinare il valore della somma scontata allora si applica una formula analoga a quella per determinare l'interesse in capitalizzazione semplice dunque:

S=C*i*t

E quindi:

V=C - S

Quindi:

V=C - S= C- C*i*t

E raccogliendo una C si ottiene la legge dello sconto commerciale:

V=C*(1-i*t)

Nello sconto commerciale si esprime il tempo c.d. commerciale che impone che un anno sia formato da 360 giorni.

Esempio:

si sconta presso una banca una cambiale da L. 2.000.000 , esigibile tra 25 giorni.

Quanto si riceve se il tasso è del 18,75%?

I dati che ho sono:

C=2.000.000

i(tasso)=0,1875 annuo;

t =25 giorni(in un anno, perché il tasso è annuo significa 25/360)

allora:

V=C*(1-i*t)

V=2.000.000*(1-0,1875*25/360)

V=2.000.000*(1-0,0130208333)

V=2.000.000*(0,9869791667)

V=1.973.958

quindi il valore attuale è di 1.973.958 e lo sconto effettuato è:

S=C-V

LO SCONTO RAZIONALE O SEMPLICE:

Per determinare con la legge di sconto razionale il valore attuale di un capitale C esigibile al tempo t si calcola la somma che, impiegata ad interesse semplice al tasso fissato i, produce nel periodo t un montante pari a C.

Allora:

C=V*(1+i*t)

Da cui:

V=C/(1+i*t)

Da cui lo sconto S =

S= V*i*t

Quindi la risoluzione degli esercizi inerenti allo sconto razionale, dunque la determinazione del valore attuale e dello sconto sono risolvibili grazie a queste poche formule, valendo tutto quanto detto in regime di capitalizzazione semplice e in particolar modo stando attenti al tasso e al tempo che devono sempre viaggiare paralleli e , nel caso dello sconto commerciale al fatto che i gioni che formano un anno in tale regime sono 360 e non 365 o 366.

A parità di tempo, capitale e tasso lo sconto razionale è minore dello sconto commerciale e quindi il valore attuale calcolato con la legge di sconto razionale è maggiore di quello che si ottiene con lo sconto commerciale: quindi per il risparmiatore conviene lo sconto razionale o semplice in quanto lo sconto sarà minore e lo stesso risparmiatore otterrà maggiore liquidità da un operazione di sconto razionale piuttosto che da un operazione di scontyo commerciale, quest'ultima più conveninete alle imprese commerciali che daranno al risparmiatore minore liquidità , lucrando maggiormente da un operazione di sconto commerciale rispetto all'applicazione dello sconto razionale(la differenza si ha non solo nei giorni che sono minori ma anche nei tassi di sconto che risultano in media essere maggiori, sempre rispetto allo sconto razionale).

Esempio:

si scontano effetti per 2.000.000, esigibili tra 25 giorni.

Quanto si riceve se il tasso è del 18,75% applicando lo sconto razionale o semplice?

I dati che ho sono:

C=2.000.000

I=(tasso)=,01875

T=25/360.

V= C/(1+i*t)=2.000.000/(1+0,1875*25/360)=2.000.000/1,013=1.974.300

S= C-V=2.000.000 - 1.974.300=25700

Confrontando i dati con il medesimo esercizio risolto però applicando lo sconto commerciale si nota che in questo caso il valore attuale è maggiore e lo sconto è minore.

LO SCONTO COMPOSTO:

Si potrebbe dire che come lo sconto semplice è analogo alla capitalizzazione semplice  anche lo sconto composto ha delle analogie alla capitalizzazione composta.

Le formule sono le seguenti:

C=V*-(1+i)^t

Da cui:

V=C/(1+i)^t

Ovvero:

V=C*(1+i)^-t

Lo sconto non è altro che C - V

Ovvero:

S= C-V=C-C(1+i)^-t=C*[1-(1+i)^-t]

Ovvero:

S=C*[1-(1+i)^-t]

Nel caso di operazioni di sconto composto il ragionamento è analogo a quello delle operazioni di capitalizzazione composta, dunque vale tutto quanto già ricordato su tasso, tempo,etc..

Esempio:

cedo il diritto a riscuotere L.7.500.000 fra 8 anni, convenendo il tasso del 12% e la legge di sconto composto.

Quale somma ricevo?

I dati che ho sono:

C=7.500.000

I(tasso)=0,12

T=8 anni

Allora:

V=C*(1+i)^-t

V=7.500.000*(1+0,12)^-8

V=7.500.000*(1,12)^-8

V=7.500.000*(0,403883228)

V=3.029.124

se il tempo è una frazione ci si comporta analogamente a come ci si comportava in regime di capitalizzazione composta ovvero:

V=C*(1+i)^-(t+f)

Dove t è il tempo intero(numero intero positivo o appartenente a Z+) e f è il numero razionale(numero razionale positivo o appartenente a Q+).