 |  | |
|
| | |
|
| |
TEORIA DEI SEGNALI
SEGNALI CERTI
GRANDEZZE ASSOCIATE AI SEGNALI (energia, potenza, media, mutua energia e potenza, invarianza per traslazione, durata convenzionale di un segnale)
SPAZI
VETTORIALI DI SEGNALI (prodotto scalare=mutua energia o potenza, segnali
ortogonali e paralleli, somme di se 414f51e gnali (Ex+y=Ex+Ey+2Re[Exy]),
basi ortogonali ed ortonormali, coordinate, norma di un segnale
, teorema di Parseval Ex,Px= |xk|2 ed Exy,Pxy= xkyk*)
SERIE E TRASFORMATA DI FOURIER (teorema di Parseval, trasformate di alcune funzioni, proprietà delle trasformate (vedi dopo), integrazione e derivazione dei segnali di energia).
CONVOLUZIONE TRA 2 SEGNALI (la trasformata è il prodotto delle trasformate, calcolo della convoluzione, proprietà: commutatività, durata T=Tx+Ty, traslazione nel tempo c(t-tx-ty)).
CORRELAZIONE PER SEGNALI DI ENERGIA (proprietà: Rxy(0)=Exy, Rxy(t)=R yx t), |Rxx(t)|<|Rxx(0)|, la trasformata dell' autocorrelazione X(f) , della mutua correlazione è X(f)Y (f) ( spettro di densità di mutua energia), invarianza per traslazioni)
CORRELAZIONE PER SEGNALI DI POTENZA: proprietà: Rxy(0)=Pxy, Rxy(t)=R yx t |Rxx(t)|<|Rxx(0)|, segnali periodici Rxy(t xk*ykej2pft F[Rxy(t)]=spettro di densità di potenza, Rxx(t) è dello stesso periodo e precisamente Rxx(t)=1/T Rgg(t-kT)
ANALISI ARMONICA GENERALIZZATA (unificazione di segnali di energia e di potenza attraverso la Rxy(t) e Sx(f), proprietà della densità spettrale Sxy(f): Sx(f)=Ex o Px, è reale, non negativa e pari, Rxy=x(t) y (-t) (o Ryx a seconda di come lo si definisce) ,
SISTEMI LINEARI:
Proprietà: sovrapposizione degli effetti ( sistema lineare), permanenza (o stazionarietà), causalità, stabilità, istantaneità (o mancanza di memoria).
Risposta
impulsiva h(t,t) cioè y(t)=T[x(t)]=
(dimostrazione) (ipotesi di stazionarietà h(t t y(t)=x(t)*y(t), causalità
, stabilità h(t) è al quadrato sommabile F[h(t)]).
funzione di trasferimento H(f)=M(f)ejj(f) (risposta in ampiezza e fase): (risposta ad un segnale armonico,sinusoidale e periodico, conseguenze dell'ipotesi di causalità sulla H(f), esempi di calcolo di H(f), H(f) nei circuiti, sistemi in serie Heq=H1 H2, in parallelo Heq=H1+H2, retroazione Heq=H1/(1-H1 H2), distorsione lineare, filtri).
Legame tra Rxx dell'ingresso e Ryy dell'uscita Ryx(t)=Rxx(t)*h(t jhh t)=h(t)*h*(-t)=funzione di autosistema, Ryy(t)=Rxx(t jhh t Sy(f)=Sx(f) H(f)
SISTEMI NON LINEARI (non si può definire h(t), aggiungono componenti frequenziali, esempi di dispositivi non lineari)
MODULAZIONE SU PORTANTI SINUSOIDALI A(t)cosy(t)=A(t)cos[2pf0t+j(t)]:
Inviluppo A(t), fase istantanea y(t) e frequenza istantanea y'(t)/2p; deviazione istantanea di fase e frequenza. In generale il segnale modulato è un passabanda, descrizione delle tre modulazioni.
Inviluppo complesso 
=A(t)ejj(t), segnale zx(t)=
e loro interpretazione ( Zx(f)=2X+(f) e 
=Zx(f+f0) con x+(t)=segnale
analitico), x+(t) si ottiene da x(t) tramite 
(x+(t)=
), x(t)=Re[zx(t)]
trasformata di hilbert: 
è un filtro HH(f)=-jsgn(f), proprietà (sono
4), è responsabile della soppressione della
parte di spettro di X(f) a frequenze negative (serve per calcolare x+(t)
in funzione di x(t)).
componenti analogiche di bassa
frequenza xc(t)+jxs(t)=: legame diretto e inverso con x(t) e (in particolare x(t)=xc(t)cos2pfxt-xs(t)sen2pfxt=doppia modulazione),
sono le antitrasf. delle parti pari e dispari di .
Interpretazione grafica di e zx(t).
Considerazioni energetiche: ( , , , <Xc Xs>=0,
).
Demodulazione in ampiezza (demodulatore normale e coerente).
Modulazione SSBs
CAMPIONAMENTO DEI SEGNALI: xc(t)= x(tk)d(t-tk) (Lo spettro del segnale campionato è Xc(f)= =Fc X(f kFc)=infinite repliche a distanza Fc dello spettro X(f), condizione di Nyquist, teorema del campionamento x(t)= x(kTc)senc(pFct kp) detto anche interpolazione del 1o ordine, campionamento con tenuta, campionamento di segnali passa-banda).
TEORIA DELLA PROBABILITA'
DEFINIZIONI: Esperimento, evento, spazio campione, probabilità di un'evento(approccio frequentistico, classico, assiomatico), 3 assiomi: P(A) 0, P(S)=1, A B P(A B)=P(A)+P(B)
PROBABILITA'
CONDIZIONATA: def. 
, A e B statisticamente indipendenti se P(B|A)=P(B) P(A,B)=P(A)P(B), teorema della probabilità totale P(M)= P(M|Ai)P(Ai), teorema di bayes.
VARIABILI ALEATORIE:
Distribuzione di probabilità Fx(x) per def. è P(x x), def. della densità di probabilità come la derivata di Fx(x
v.aleatorie discrete:
v.binomiale
(numero di successi su n prove) fx(x)=
mx=np
v.di
poisson (n°di successi su n
prove con p 0
e np l)
fx(x)=
mx=l
2 v.gaussiana
fx(x)=
v.aleatorie continue
v.uniforme fx(x)=
v.di cauchy fx(x)=
5 v.di rice fx(x)=
(con I0=
=funzione di Bessel)
6 v.esponenziale monolatera: fx(x)=le-lxu-1(x)
(m=1/l s l ),
bilatera: fx(x)=
(m=0 s l
7 v.gamma fx(x)=
con 
=(b-1)!
(per b=1
si ottiene l'espon.monolatera) invece per b=n=intero
si ottiene la v.di erlang
mentre per b=n/2
e a=1/2
si ottiene la v.chi-quadro.
composizione
di var. aleat. (h=g(x)
assume g(x1) con la prob. con cui x
assume x1: es. h x )
localmente, per f.monotone si ha: fh(y)=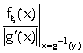
,per operazioni lineari h=ax+b: fh(y)= 
momenti E[xn]
e E[(x m)n]
m1=valor medio, m2=valore quadratico medio, m m s =varianza
=m2 m2,
se fx(x)
pari
m2n+1=0 e m2n+1=0,
mediana e moda, mn=
e mn=
, skewness (simmetria) e kurtosis (gaussianità).
funzione caratteristica C(u)=
=E[ejux]
(è un'antitr.di Fourier, fx(x)=
), caso discreto C(u)= Pkejuk,
Cx(0)=1
(cond.di normalizzazione), f.caratteristiche di variabili aleatorie particolari
(cauchy e gaussiana), proprietà: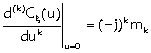 
e 
.
VARIABILI ALEATORIE BIDIMENSIONALI
Def distribuzione congiunta Fxh(x,y), distr.marginale Fxh(x,+ ), densità congiunta, densità marginale.
Per eventi indipendenti (vedi probabilità condizionata) Fxh(x,y)=Fx(x)Fh(y) e, derivando, vale anche fxh(x,y)=fx(x)fh(y).
Variabili aleatorie congiuntamente gaussiane (le densità marginali sono gaussiane).
Momento congiunto mij=E[xihj],
m. centrale congiunto mij=E[(x mx)i(h my)j],
m11=E[xh]=correlazione, m =Cov(x h)=covarianza, r=
=coefficiente di correlazione r r h ax+b
con a>0, r incorrelate,
E[x h ortogonali,
x h
indipendenti
incorrelate (" "
vale per le congiuntamente gaussiane), cov(x h)=corr(x h mxmy.
TRASFORMAZIONI DI VAR. ALEAT. BIDIMENSIONALI
Composizioni di due
variabili in una: w x h
(+caso gaussiano), w xh w x h w=
, w=max(x h w=min(x h
Doppia trasformazione 
, teorema fwz(w,z)=
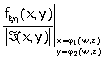
linearità del momento e[ ]: se h=g(x E[h g(x)fx(x)dx, e se w=g(x h E[w g(x,y)fxh(x,y)dxdy, da ciò si dimostra che E[ax+bh]=aE[x]+bE[h
VARIABILI ALEATORIE CONDIZIONATE: def.analoga alla probabilità condizionata Fx|B(x|B)=P(x x,B)/P(B),
B="h y" Fx(x|h y) e fx(x|h y) che è la derivata
B="h=y"="y h y+dy" Fx(x|y) e fx(x|y)
Proprietà analoghe alla probabilità condizionata.
VARIABILI ALEATORIE N-DIMENSIONALI: matrici R, C e M, proprietà R - MTM = C
TEOREMA LIMITE CENTRALE
PROCESSI ALEATORI
DEFINIZIONI(Tempo/stato-continui e discreti, statistiche=distribuzioni e densità del n ordine)
PROPRIETA'
Del 1°ordine: valor medio mx(t)= xf(x,t)dx=E[X(t)], Potenza Px(t)=E[X2(t)], varianza m (t)=sx (t)=Px(t) mx2(t).
Del 2°ordine:autocorrelazione Rxx(t1,t2)=E[X(t1)X(t2)], (potenza Px(t)=E[X2(t)]=Rxx(t,t)), autocovarianza Cxx(t1,t2)=Rxx(t1,t2) m(t1)m(t2), (varianza sx (t)=Px(t) mx2(t)= Cxx(t,t)).
In generale per le statistiche di ordine n: Momento mhk(t1,t2)=E[X1hX2k], Momento centrale mhk(t1,t2)= =E[(X1 m1)h(X2 m2)k]
Per le mutue statistiche del 2°ordine: Mutua Correlazione Rxy(t1,t2)=E[X(t1)Y(t2)],Mutua Covarianza Cxy(t1,t2)=. , Coefficiente di Correlazione rxy(t1,t2)=Cxy(t1,t2)/sx(t1)sy(t2), (stesse proprietà del rxy delle var. aleatorie).
ESTENSIONE AI PROCESSI COMPLESSI: Rxx(t1,t2)=E[X1X2*]=Rxx*(t2,t1),Px(t)=E[|X(t)|2],Cxx(t1,t2)=Rxx(t1,t2) m(t1)m*(t2) (analogamente Rxy e Cxy)
PROCESSI STAZIONARI
SSS se f.di densità dipende dalle n-1 tn-tn-1, . ,t2-t1, proprietà: stazionarietà di grado n stazionarietà di grado 1.n-1, SSS di grado 1 mx,s x,Px,mx=cost. , SSS di grado 2 Rxx(t), Cxx(t)=Rxx(t mx2
SSL se mx(t)=cost. e Rxx(t1,t2)=Rxx(t
Rxx(0)=Px=Rxx(t,t)=Px(t), Cxx(0)=sx =Cxx(t,t) un processo SSL ha una potenza fissa
Estensione ai proc. complessi Rxx(t)=E[X(t)X (t-t)], Cxx(t)=Rxx(t |mx|2 (analogia coi segnali certi).
Proc. congiuntamente SSL se Rxy(t), processi mutuamente ortogonali se Rxy(0)=0, incorrelati se Rxy(t
Altre
proprietà: 
(non vale sempre), Ryx(t)=Rxy*(-t),
Cyx(t)=Cxy*(-t),
Z(t)=X(t)+Y(t) è SSL se lo sono X(t) e Y(t), Pz=Px+Py+Pxy+Pyx
ESEMPI DI PROCESSI ALEATORI
proc. normale(gaussiano): X(t) congiuntamente gaussiane per ogni t1.tn, completamente determinato da mx(t) e Cxx(t1,t2), unico caso in cui SSL SSS (dimostrazione).
proc. bianco: Cxx(t)=Rxx(t)=kd t), mx=0, X(ti) e X(tj) sono incorrelate per ogni ti tj perché C(ti,tj)=0, Px=R(t,t)=R(0)=+ sx , passaggio in un sistema lineare Cyy(t)=kjhh t
proc. armonico: X(t)=Acos(2pf0t+q) con q uniforme in [0,2p] con A e q indipendenti; è SSL.
proc. di poisson: (pag 290)
segnale telegrafico: X(t)=1 se in (0,t) cadono 2n punti e -1 se cadono 2n+1 punti distribuiti secondo Poisson di parametro l=intensità dei punti.
onda pam non stazionaria
TRANSITO DEI PROCESSI ALEATORI NEI SISTEMI T[x(t,xi)]=y(t,xi
Sistemi (lineari e non) istantanei: Y(t)=g[X(t)] (per le v.al. era h=g(x)), per l'istantaneità del sistema, si può calcolare fY(y,t) in funz.di fX(x,t) analogamente alle v.al. (vedi composizione), my(t)=E[Y(t)]=E= = g(x)fX(x,t)dx, Ryy(t1,t2)=E[Y(t1)Y(t2)]=E[g[X(t1)]g[X(t2)]]= g(x1)g(x2)fX1X2(x1,x2,t1,t2)dx1dx2, X(t) SSS di ordine n Y(t) è SSS dello stesso ordine, mentre X(t) SSL Y(t) SSL, esempio del quadratore.
Sistemi
lineari e permanenti: Y(t)=X(t) h(t)
(operano solo sulla t quindi le v.al.sono come dei coefficienti) X(t) gaussiano
Y(t) gaussiano, my(t)=mx(t) h(t)=g[mx(t)]
se SSL
my=mxH(0), Rxy(t1,t2)=Rxx(t1,t2) h(t2)
(=g[Rxx] considerando come variabile t2), Ryy(t1,t2)=Rxx(t1,t2) h(t1) h(t2),
se X(t) è SSL, nel caso complesso, si ha Rxy(t)=Rxx(t h t)
e Ryy(t)=Rxx(t h(t h t
Y(t) è SSL e X(t) e Y(t) sono congiuntamente SSL, (si ragiona analogam. per Cyy).
SPETTRO DI UN PROCESSO SSL :
Scxx(f)=F[Cxx(t)] (spettro di densità di covarianza)
Sxx(f)=F[Rxx(t F[Cxx(t)+mx2]=Scxx(f)+mx2d(f) (=PX(f) spettro di densità di potenza), (1) Sxx(f) 0, (2) Sxx(f) è reale perché Rxx(t)=R xx t P(f)df=Rxx(0)=Px=E[X2(t)].
Sxy(f)=Sx(f)H (f), Sy(f)=Sx(f)|H(f)|2 Py=Ryy(0)= Sx(f)|H(f)|2df.
PROCESSI CICLOSTAZIONARI: def CSSS: fX1..Xn(x1.xn,t1.tn)=fX1..Xn(x1.xn,t1+kT,.,tn+kT), def CSSL: mx(t)=mx(t+kT) e Rxx(t1,t2)=Rxx(t1+kT,t2+kT), teorema 1 (Y(t)=X(t-q)): CSSS SSS e CSSL SSL (applicazione al proc. armonico e all'onda p.a.m.)
PROCESSI ERGODICI IN MEDIA: medie delle f. membro m(k)=m(i)=mx(t)=mx
I cond.nec.e suff.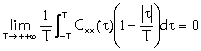 
II cond.suff. |Cxx(t)|dt<+
III cond.suff. 
teorema di slutsky
PROCESSI ERGODICI IN CORRELAZIONE: le ri(t) sono tutte uguali a Rxx(t
PROCESSI ERGODICI IN DISTRIBUZIONE:
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
