Serie di Fourier

tecnica

Serie di Fourier :

Se f(x) è una funzione continua a tratti nell'intervallo [0,2p] e pensata ripetuta periodicamente la si può rappresentare tramite la serie di Fourier:

Per il teorema dell'espressione dei coefficienti si ha:

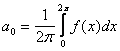
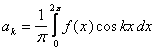
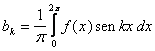
Scrivere la serie di Fourier per la funzione periodica di periodo 2p, che nel tratto [-p p definita da

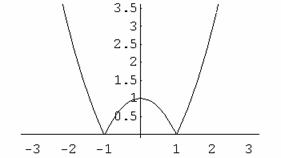
Essendo f(x) una funzione pari, la serie di Fourier relativa ad essa risulterà costituita da soli coseni.

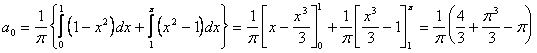
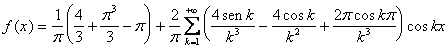
Essendo la funzione derivabile in tutti i punti dell'intervallo, si ha sempre la convergenza ad f(x).
Scrivere la serie di Fourier per la funzione:

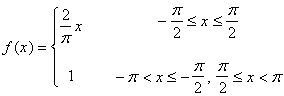
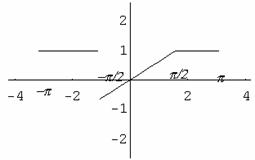
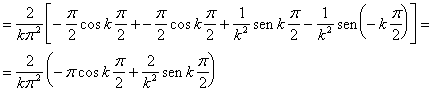
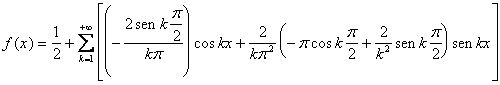
Si scriva la serie di Fourier relativa alla funzione di periodo 2p, così definita e se ne calcoli la somma per x=0 e per x=p

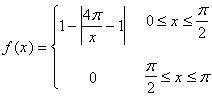
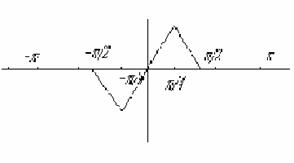
La funzione è dispari quindi la serie di Fourier risulterà costituita da soli seni:

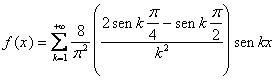
La serie, limitatamente all'intervallo [-p p], converge ad f(x), ed ha come somma per x=0 il valore 0 , e nel punto x=p ancora il valore 0.
Si scriva la serie di Fourier relativa alla funzione di periodo 2p, così definita:

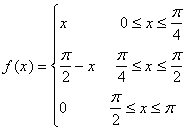
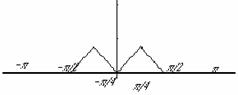
La funzione è pari, quindi la serie di Fourier ad essa relativa avrà solo coseni:

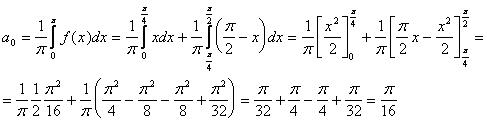
La serie, limitatamente all'intervallo [-p p] converge ad f(x).

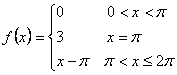
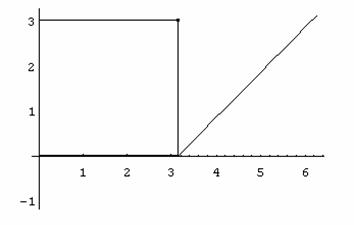
La funzione , non essendo

nè pari nè dispari, si scriverà come

serie di Fourier avente sia seni

che coseni. Dunque la serie

si scriverà sotto la forma

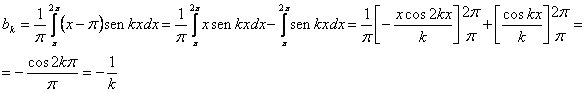
La serie può essere dunque scritta come:

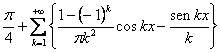
La serie converge per qualunque valore di x, perché la è derivabile in tutti i punti di continuità, e nei punti che sono singolari, ha derivata a destra e a sinistra .

Converge ad nei punti di continuità ossia nell'intervallo

mentre converge a nei punti ; converge a 0 nel punto

Serie di Taylor :

Dare una stima del numero "e" con otto cifre decimali esatte

Scrivere lo sviluppo in serie di MacLaurin per la funzione

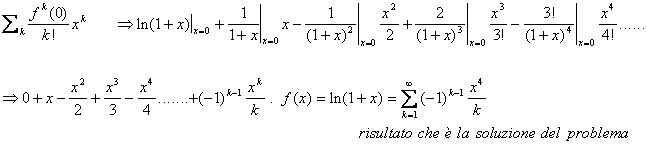
Fornire una stima di sen0.5 con un errore non superiore ad un millesimo

Per dare una stima di questo numero posso usufruire dello sviluppo della funzione seno

in serie di MacLaurin calcolata in x=0,5

sen x=

Scrivendo   il resto 2n+1-esimo e imponendolo minore di 0,001 si ottiene una valutazione del

resto non superiore ad un millesimo :

si ha nella formulazione di Lagrange (-1) trattandosi di angoli

molto piccoli (si ricordi che ) la funzione coseno è approssimabile senza errori

significativi a 1. Si conclude che:

Calcolare la derivata ottava nel punto x=0 per la funzione:

Problemi di convergenza di serie :

1) Studiare la convergenza puntuale ed uniforme nelle seguenti serie:

Si tratta di una serie geometrica di ragione q=

Essa converge se <1;ovvero se: con la condizione di realtà:

; ; ; ;;

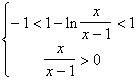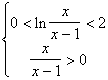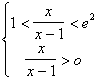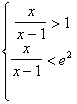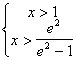La serie risulta convergente nell'aperto 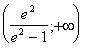  ;divergente per altri valori di x che rendono reale il logaritmo.

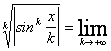
Essendo il limite minore di 1 la serie e' assolutamente convergente in modo indipendente da X; si ha anche convergenza uniforme.