Approccio exergetico ed exergia

essendo T la temperatura alla quale è disponibile l' energia in questione e T_a una temperatura qualsivoglia di riferimento: per comodità la minima del processo, oppure quella ambiente.

Il concetto di exergia trova prevalente applicazione nello studio dei bilanci energetici degli impianti motori a flusso continuo di fluido.

Gli scambi di calore, negli impianti in argomento, avvengono sempre a pressione praticamente costante (in generatori di vapore, condensatori, scambiatori, rigeneratori, ecc.) e pertanto le acquisizioni o cessioni di calore da parte di un fluido sono acquisizioni o cessioni di entalpia.

L' exergia W connessa con l' energia termica Q scambiata assunta T_u quale temperatura di riferimento, vale, in termini differenziali, per la precedente definizione:

dove è detto fattore di Carnot.

Conseguentemente in una trasformazione che conduca il fluido dallo stato a ad un generico stato b:

e con riferimento all' unità di massa:

W_ab = Q_ab - T_a(S_b - S_a) = i_ab - T_a(S_b - S_a)

trasformazione a pressione costante.

Il contenuto exergetico acquisito durante il riscaldamento isobaro a-b è dunque pari al lavoro complessivamente ottenibile facendo espandere il fluido stesso isoentropicamente dallo stato b raggiunto fino alla temperatura T_a e riconducendolo poi allo stato iniziale per via isoterma.

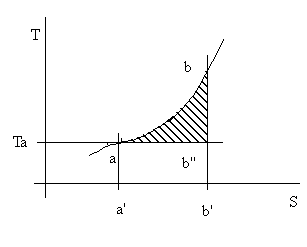
figura 4.1

Con riferimento alla figura 4.1:

Q_ab = area aa'bb';

T_a(S_b - S_a) = area a'ab''b';

exergia acquisita dal fluido: area abb'.

Ogni scambio di calore, che necessariamente avviene da un fluido più caldo ad un fluido più freddo (in pratica con salti di temperatura spesso rilevanti, per ridurre la superificie di scambio) si produce una degradazione dell' energia e cioè una riduzione della frazione utilizzabile. Valutiamo l' abbassamento di exergia in un caso semplice. Consideriamo lo scambio di calore elementare dQ da un gas ad un vapore rispettivamente alle temperature attuali T_g e T_v

( con _Tv > T_g). La variazione di entalpia del sistema che accompagna tale scambio è:

da cui:

e la corrispondente perdita di energia utilizzabile risulta:

Da questa espressione si può determinare la perdita di energia utilizzabile W, ad es. mediante un calcolo alle differenze finite, valutando ad ogni passo il valore attuale di T_g e T_v.

La stessa espressione finale è determinabile con la definizione dell' exergia W vista in precedenza:

dW = dQ

dove:

dW è l' incremento di exergia del sistema;

dQ è fornita dal mio sistema al fluido.

W = W_v + W_g =

= W_vf - W_vi + W_{gf -} W_gi

= _v Q_gv + _g Q_vg

= -(_{g - v})Q_gv

Il segno meno nell' ultimo membro è dovuto al fatto che si tratta di una perdita di energia.

Nel nostro caso:

dW = _gdQ_g + _vdQ_v =

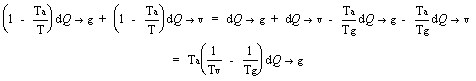
Siccome la parentesi è negativa mentre dQ_{g è positivo segue che dW < 0 cioè si ha una perdita di exergia.}

In conclusione, utilizzando il concetto di exergia è possibile stendere il bilancio di un impianto in forma termodinamicamente più significativa di quanto può essere derivato dalla considerazione della prima equivalenza tra calore e lavoro, e cioè dal solo I principio.