|
|
| |
I mercati finanziari
Le obbligazioni sono un contratto in cui un soggetto si impegna, dopo un lasso di tempo, a restituire il capitale a lui prestato, garantendo anche un certo interesse a scadenze prefissate.
Le obbligazioni zero coupon sono titoli che non pagano cedole (ad es.: compro a 20 e fra 30 anni mi rimborsano 100).
Le obbligazioni console, al contrario, non rimborsano ma garantiscono un interesse fisso (ad es.: pagando 100, non si avrà mai diritto al rimborso, bensì ad un interesse annuo di 4).
Rischi delle obbligazioni: 1. di default/di insolvenza/bancarotta (dipende dalla solvibilità dell’emittente): è il rischio che il titolo non venga rimborsato totalmente come pattuito 2. evoluzioni del prezzo di mercato 3. La maturità/durata (breve/medio/lungo) 4. tasso di rendimento (può essere fisso o variabile; Il tasso forward è il tasso di interesse futuro ch 848b15i e il mercato si aspetta oggi) 5. valuta (es.: €/$ etc.)
Nota: La relazione tra rendimento e maturità genera .
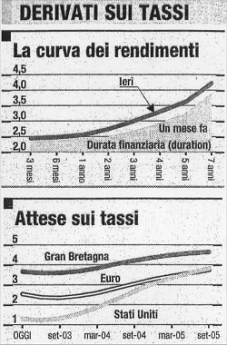
. La curva dei rendimenti (elaborazione relativa ai prezzi dei futures su tassi a breve termine, pubblicata ogni giorno su “Il sole 24 ore”)
Rt > rt => rt ↑ => Ptitoli a breve ↓. Al contrario, se la curva fosse negativamente inclinata, i mercati finanziari si aspetterebbero che i tassi di interesse a breve diminuiranno.
Modello semplificato: immaginiamo di avere a che fare con due tipi di BOT: scadenza ad un periodo oppure 2 periodi.
(Ricordiamo che i BOT non hanno cedola, ma soltanto un rimborso facciale, ad es.: 100, ed un prezzo d’acquisto inferiore ad esso, ad es.: 98: alla scadenza si ritireranno 100/100 dopo averli pagati 98/100).
Supponiamo anche che non esista incertezza nei mercati, per cui il futuro sia certo.
L’operatore che ha esigenze di liquidità a breve ha di fronte a sé una scelta tra due opzioni: comprare un titolo a breve (1 periodo) oppure un comprare un titolo a medio/lungo (2 periodi) per poi rivenderlo a breve.
Dati:
Rt = tasso d’interesse annuo sul titolo con durata 2 periodi
rt = “ “ “ “ “ “ “ 1 periodo
P1t = prezzi al tempo t del titolo a breve (1 periodo)
P2t = “ “ “ “ “ “ “ lungo (2 periodi)
Ht = rendimento ottenuto detenendo per 1 periodo un titolo di durata 2 periodi.
![]() 1 rimborso alla scadenza (base unitaria)
1 rimborso alla scadenza (base unitaria)
1 + rt ≡ -----
![]() P1t
prezzo d’acquisto (ad es.: 0,98)
P1t
prezzo d’acquisto (ad es.: 0,98)
Ne consegue:
P1t+1 = 1 / (1 + rt+1)
P2t = 1 / (1 + Rt
P1t+1 1 / (1 + rt+1) (1+Rt)2 poichè “R“ e “r“ sono entrambi numeri “piccoli“ allora
1 + Ht ≡ ------ sostituendo: ----- ----- ------- = ------------- possiamo fare una “approssimazione logaritmica“ e soste-
P2t 1 / (1 + rt)2 1 + rt+1 nere quanto segue : Ht ≈ 2 Rt – rt+1
rt = Ht
rt = 2 Rt – rt+1
Rt = (rt + rt+1) / 2
Sottraendo da entrambi i lati rt giungiamo ad un’importante conclusione:

![]() rt+1
= E = aspettativa
rt+1
= E = aspettativa
rt+1 – rt
Rt – rt = --------- ovvero: la differenza tra i tassi è uguale alla loro media.
2 Questa equazione potrebbe essere rilevante ai fini dell’esame (ecco perché è importante) J
se rt > Ht => P1t ↑ => rt ↓ => la curva dei rendimenti sarà crescente!
Se il tasso degli investimenti a lungo termine è superiore rispetto a quelli a breve, questo potrebbe indurci a pensare (erroneamente) che convenga comprare dei titoli a lungo (con tasso superiore) per poi rivenderli a breve.
In realtà non è così semplice, visto che, dopo un periodo soltanto, si potrà incassare un valore inferiore rispetto a quello del rimborso finale. Poiché abbiamo ipotizzato la certezza dei mercati, la scelta sarà totalmente indifferente: il rimborso inferiore compenserà il tasso superiore.
Le azioni
Sono quote rappresentative del capitale proprio della società, attribuendo al proprietario dell’azione la qualifica di socio o azionista. Il valore di mercato delle azioni dipende da molti fattori, in particolare dalle aspettative di crescita della società e dalle variazioni del mercato: (Pt+1 + dt) / Pt (d = dividendo, P = prezzo t = tempo).
Il prezzo di un titolo, inoltre, varia inversamente al tasso di interesse nominale corrente.
Se le azioni scendono significa che, al P di ieri, c’era un eccesso di offerta ed il prezzo dovrà scendere fino a tornare al punto di equilibrio con la domanda. Esempio:
|
Ultimo Prezzo: 12,67 |
Quantità per le quali si è disposti a vendere/comprare |
|
Denaro (P al quale vengono domandate le azioni): 12,65 |
|
|
Lettera (P al quale vengono offerte le azioni): 12,68 |
|
Le holding (le scatole cinesi)
Società A (1.000 € capitale sociale) emette capitale => Società B acquisisce il 50%+1 delle azioni di A => Società C acquisisce il 50%+1 delle azioni di B.
Le società B e C sono holding. La società C controlla sia B sia A, ma con un capitale di soltanto 251 €.
La società C acquista un bene a 100 e lo rivende ad A a 1.000, per trasferire gli utili da A a C ed eludere gli interessi dei piccoli azionisti (azionariato diffuso: Mkt che è, comunque proprietario di 749 € su 1.000!).
Il mercato azionario
Con le azioni non c’è obbligo di rimborso del capitale.
Es: se compro 100 e vendo a 110
NOTA BENE: (Pt+1 + Dt+1) / Pt ≡ 1 + Ht dove Ht è il rendimento ottenuto e D è il dividendo, Pt+1 il capital gain.
Le aspettative sul prezzo delle azioni
Gli esiti aggregati dipendono dalle aspettative aggregate. Le opinioni comuni tendono spesso a non realizzarsi: se tutti pensassero che certe azioni potranno salire in futuro, è probabile che le abbiano già comprate tutte, per cui in futuro non potranno che scendere.
Et (1 + Ht) = 1 + r r è costante per semplificazione.
“La mia
aspettativa oggi, riguardo alla mia aspettativa di domani per dopodomani, è
uguale alla mia aspettativa oggi per dopodomani.” Iterando questo
ragionamento all’infinito giungiamo alla formula del “NOTA BENE”.
Con una previsione
perfetta (perfect forsight) le aspettative si realizzano sempre (ex post). In
un mondo stocastico, però, la previsione non è mai perfetta. L’aspettativa
razionale, invece, è una situazione nella quale tutta l’informazione
disponibile è usata per avvicinarsi il più possibile alla realtà, senza
commettere errori sistematici (ovvero imparando dai propri errori).
![]() Et [(Pt+1 + Dt+1) / Pt
] = 1 + r
Et [(Pt+1 + Dt+1) / Pt
] = 1 + r
1/ Pt * E [Pt+1 + Dt+1] = 1 + r
poiché l’aspettativa di una somma è la somma delle aspettative .
![]()
Pt = [1 / (1 + r)] * Et (Pt + 1) + [1 / (1+ r)] * Et (Dt+1)
Ma se è vero al tempo t assumiamo allora che sia vera anche al tempo t+1.
![]() Per cui consegue che = Et+1(Pt+2). (Bootstrap di equilibrio: il
valore di una variabile non dipende da altre variabili, ma dal valore attuale
della variabile stessa).
Per cui consegue che = Et+1(Pt+2). (Bootstrap di equilibrio: il
valore di una variabile non dipende da altre variabili, ma dal valore attuale
della variabile stessa).
Questo è vero a meno che non giungano altre informazioni aggiuntive che costituiscono una SORPRESA che modificherà le aspettative: la teoria dei mercati efficienti sostiene, appunto, che un mercato è considerato efficiente se il Prezzo riflette tutta l’informazione disponibile e rilevante, oppure se tutte le variazioni di Prezzi sono esogene e prive di inerzia. In un mercato efficiente il valore delle azioni dipende esclusivamente dal sopraggiungere di nuove informazioni sui dividendi futuri. questa parte è denominata Bt
Ovvero: Valore
fondamentale + Termine di bolla (Bt) = Prezzo delle azioni
![]()
 NOTA BENE
NOTA BENE
![]()
![]() ∞ 1 J
Et * Pt + T
∞ 1 J
Et * Pt + T
Pt = ------- * Dt+1 + lim
J=1 1 + r T ∞ (1 + r) T
Secondo la finanza classica Bt = 0, quindi Pt dipende dal valore attuale della somma dei dividendi attesi scontati (e da r).
Questo significa, in poche parole, che il valore FONDAMENTALE di un’impresa dipende esclusivamente dalla sua capacità di generare profitti. Da ciò deriva la teoria del “Buy & Hold” (compra e detieni), che sostiene che non abbia senso vendere le azioni perché il loro rendimento è certo (l’informazione non è costosa, gli agenti sono totalmente razionali e le variabili passate non influenzano quelle future).
Gli elementi empirici che hanno messo in crisi questa teoria sono stati i “crash” dei mercati (ad es.: il crash dell’Ottobre ’87, quando non ci fu nessuna notizia, ex ante, che fosse in grado di spiegare perché, nel giro di poche ore, il mercato fosse collassato).
Secondo la finanza moderna, infatti, Bt è un cosiddetto termine di bolla, per cui il P delle azioni può salire in maniera eccessiva (overshooting) rispetto al loro valore fondamentale (reale), generando una reazione anch’essa eccessiva (overreaction).
LA BOLLA SPECULATIVA (riguarda una speculazione sulle aspettative dei Prezzi e non più sui dividendi).
Essa è possibile innanzitutto poiché il prezzo delle azioni non ha tetto: se esistesse, nessuno comprerebbe le azioni perché, ragionando all’indietro, la dinamica di bolla morirebbe (la bolla scoppierebbe) sul nascere.
Nessuno riterrà conveniente comprare al tempo t9, sapendo che al tempo t10 si giungerà al tetto massimo (oltre il quale non si potranno generare profitti). Ma, sapendo che al tempo t9 le azioni saranno vendute, non verranno comprate neppure al tempo t8 e così via.
Molti economisti sostengono che il prezzo delle azioni non è sempre uguale al loro valore fondamentale, ma che a volte esse sono sopra o sottovalutate, e che una sopravalutazione, prima o poi deve cessare e generare un tracollo (scoppio).
Questo accade anche se la condizione di arbitraggio (che sostiene non esista profitto a rischio nullo) è soddisfatta.
Le bolle speculative razionali
Il prezzo delle azioni potrebbe aumentare semplicemente perché gli operatori se lo aspettano. Essi continuano a comportarsi razionalmente, pur essendo coscienti di trovarsi in presenza di una bolla speculativa.
Le fads
Il prezzo delle azioni potrebbe aumentare anche soltanto per il fatto che sono già aumentate in passato.
Queste deviazioni dal loro valore fondamentale sono denominate fads (mode).
Lo scoppio della bolla speculativa e la curva IS-LM
Esempio: il Nasdaq, dopo il boom delle speculazioni su internet, ha subito un ridimensionamento in negativo.
IS1 = anni del boom di internet
IS2 = scoppio della bolla
LM2 = Greenspan (direttore della “Federal Reserve”) per contrastare lo scoppio e mantenere costante Y (E0 = E2) ha abbassato la LM abbassando il tasso di sconto: ha aumentato l’offerta di moneta e ha spostato la Ms verso destra.



 LM2
LM2
 i0 E0
i0 E0
![]()
i2 E2 IS IS1
IS2
![]() Y
Y
![]()

|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025