Variabile statistica funzione di un'altra

tecnica

LEZIONE #2

Variabile statistica funzione di un'altra

Nella pratica puo' essere utile, nota la distribuzione di una caratteristica in una popolazione, ricavare quella di un'altra caratteristica  funzione della prima, senza ricorrere ad una ulteriore indagine sulla popolazione.

Esempi di variabili satistiche funzioni di un'altra li abbiamo implicitamente introdotti quando abbiamo calcolato la varianza della X, parlando della variabile scarto V=X-m_X e del suo quadrato V²=(X-m_X)². Usiamo la variabile V² calcoliamone la distribuzione di frequenza.

Data una trasformazione tra variabili statistiche occorre in primo luogo ricavare i valori argomentali della nuova distribuzione, quindi riordinarli e calcolarne le frequenze ricavandole da quelle della X.

Sia, ad esempio

i valori argomentali della variabile scarto e del suo  quadrato , essendo m_X=3 saranno:

Che, ordinati in ordine crescente saranno:

Per concludere la trasformazione, calcoliamo le frequenze relative della variabile V². Il valore argomentale 0 si presenta quando X assume il valore argomentale 3, come si vede dalla tabella di trasformazione dei valori argomentali. La frequenza relativa del valore 3 nella popolazione e dunque del valore 0 sara' la stessa, pari cioe' a 1/5. Il vaore argomentale 1, invece, si presenta sia quando X assume il valore 2 che quando assume il valore 4. La frequenza allora di 1 sara' pari alla frequenza di 2 piu' la frequenza di 4, pari cioe' a 1/5+1/5=2/5. Analogamente la frequenza del valore 4 sara' pari a 2/5.

Detto v_i²  l'iesimo valore argomentale della variabile V e f_i' la corrispondente frequenza relativa, questa si ottiene sommando le frequenze relative dei valori argomentali della X che si trasformano in v_i².

In seguito indicheremo la trasformazione tra le variabili statistiche X e Y, lineare o non lineare che sia, come Y=g(X).

L'operatore media M

Data una variabile statistica monodimensionale (la caratteristica e' una sola) si puo' definire l'operatore media M_X[ ], come quell'operatore che applicato ad X o a una funzione di X ne restituisce la media pesata con le frequenze relative di X

la media di X e' dunque l'operatore media applicato a X

la varianza di X e' ottenuta applicando l'operatore media alla funzione di X , g(X)=(X-m_X)²

Teorema della media

Sia Y=g(X). La media di Y si ottiene applicando l'operatore media M_Y alla variabile Y, ovvero facendo la media pesata sulle frequenze di Y. Cio' presuppone il calcolo di tali frequenze a partire da quelle della variabile X. Il teorema della media ci permette di calcolare la media di Y senza calcolarne le frequenze per tale teorema infatti

Il teorema si dimostra facilmente nel caso di trasformazioni di variabili statistiche.

Sia

Sia Y=g(X)=(X-m_X)², trasformazione non lineare. I valori argomentali della variabile Y in corrispondenza ai valori crescenti della X, con le rispettive frequenze sono:

Se ci fermassimo a questo stadio della trasformazione, ovvero non riordinassimo i valori argomentali della variabile Y, ne calcoleremmo la media nel seguente modo:

m_Y = 4

= g(x₁) f₁+ g(x₂) f₂ + g(x₃) f₃ + g(x₄) f₄ +g(x₅) f₅=

dopo il riordino, essendo g(x₁)=g(x₅) e g(x₂)=g(x₄), si ha

e la media viene calcolata come:

m_Y= 0 0.4=g(x₃)f'₁+g(x₂)f'₂+g(x₁)f'₃

che tornando indietro nella trasformazione si dimostra essere  pari alla media calcolata prima del riordino, infatti

g(x₃)f'₁+g(x₂)f'₂+g(x₁)f'₃= g(x₃)f₃+g(x₂)(f₂+f₄)+g(x₁)(f₁+f₅)=

= g(x₃)f₃+g(x₂)f₂+ g(x₂)f₄+g(x₁)f₁+ g(x₁)f₅= g(x₃)f₃+g(x₂)f₂+ g(x₄)f₄+g(x₁)f₁+ g(x₅)f₅

Altre proprieta' dell'operatore media

L'operatore media e' lineare, ovvero, in una dimensione,

M_X=aM_X+b

Infatti:

Se  a g(x_{i )} b   " x_i

a M_X[g(X)] b

Infatti:

In particolare se x_i allora M_X[X]

Se x_i 0 & M_X[X]=0

allora la variabile statistica assume solo il valore 0 con frequenza relativa1
Infatti da , poiche'
si ricava necessariamente che se necessariamente  ; poiche' almeno una delle f_i e' diversa da zero, essendo , tale frequenza sara' in corrispondenza del valore x_i=0, e assumera' il valore 1.

Se g(x_i) h(x_i)    " x_i

M_X[g(X)] M_X[h(X)]

La varianza e il teorema di Tchebychev.

La varianza delle variabile statistica X , come abbiamo gia' visto, e' data da:

In base alla prima delle propireta' dell'operatore media,

Vale inoltre il seguente teorema (Tchebycev):

La frequenza relativa degli x_i  per cui , ovvero dei valori argomentali di X compresi nell'intervallo [(m_X-ls_X), (m_X+ls_X)], e' maggiore di

Quindi la frequenza relativa dei valori argomentali compresi nell'intervallo [(m_X-3s_X), (m_X+3s_X)] e' sempre maggiore di 0.89, qualunque si la distribuzione di frequenza.

Dimostrazione

Sia h(x_i)=(x_i-m_X)², insieme di punti giacenti su una parabola con concavita' verso l'alto e vertice in (m_X,0).

Costruiamo una funzione di X, g(X) che sia minore di h per qualunque valore di x_i.

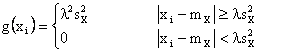
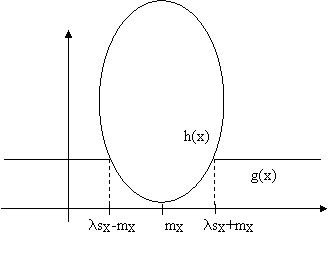
Per le proprieta' della media

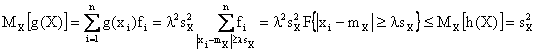
ovvero