Corso di laurea in Ingegneria Meccanica I

Fisica II

Laboratorio di fisica

Studio delle oscillazioni forzate in un circuito RCL

Indice

Nozioni sui circuiti RCL.......... ..... ...... .......... ..... ...... ...................... 2

Esperienza:misura di C e L.......... ..... ...... .......... ..... ...... .................. 6

Calcolo dell'errore.......... ..... ...... .......... ..... ...... ............................. 7

Modalità di esecuzione.......... ..... ...... .......... ..... ...... ....................... 8

Calcoli per determinare i valori di L, C e dell'errore.......... ..... ...... ...........

Commenti ed osservazioni.......... ..... ...... .......... ..... ...... ................ 11

Nozioni sui circuiti RCL

Consideriamo il circuito RCL indicato in fig.1:

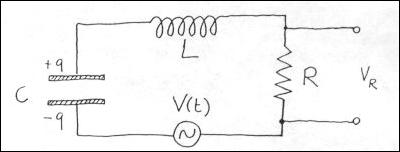
fig.1

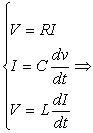
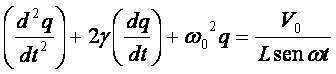
in cui:

troviamo la soluzione:

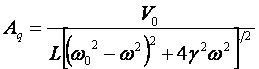
che sostituendo nella (1):

e:

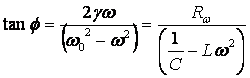
Così possiamo fare delle considerazioni:

ad una sollecitazione sinusoidale l'oscillatore armonico risponde con uno spostamento sinusoidale: la pulsazione non è quella propria w bensì quella voluta w , impressa dall'esterno; lo spostamento è sfasato rispetto alla forza; la risposta dell'oscillatore non è la stessa qualunque sia w : ampiezza e fase dipendono dal valore di w; A_q e f non dipendono dalle condizioni iniziali; soltanto le costanti a e b della parte transitoria sono legate allo stato iniziale del sistema.

In fig.2 è rappresentata la funzione A_q(w) per 4 diversi valori di resistenza del circuito crescenti da A_q1 a A_q4:

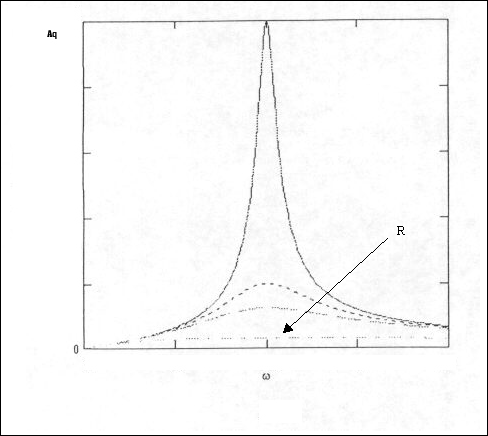
fig.2

Nel nostro caso quella che viene misurata è la tensione ai capi del resistore quindi calcolando l'andamento della corrente nel circuito:

In cui l'ampiezza della corrente è data da A_i= wA_q

Possiamo scrivere la (2) come:

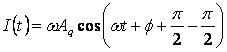
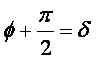
In cui :

E per le formule degli angoli associati otteniamo:

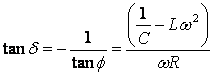
Infine la d.d.p ai capi della resistenza R sarà:

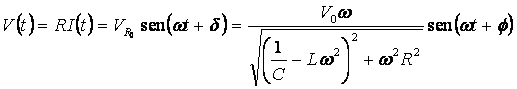
Ponendo:

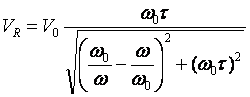
Si ha:

Posto w w = y il massimo si ha per 2(1/y-y)(-1/y²-1)=0

Quindi per y=1, w w , nel qual caso si ha V_R/V₀=1

Esperienza: misura di C ed L

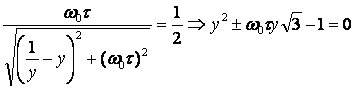
Si studia ora per quali valori di w si ha un dimezzamento dell'ampiezza. Dev'essere:

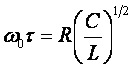
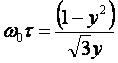
da qui:

E' possibile verificare che i due valori di w t ricavati dai due valori di y sono coincidenti:

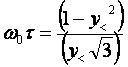
Dalla misura della frequenza in cui c'è il massimo dell'ampiezza si ottiene w e dalla y_< o y_> ( o la media di entrambe) si ottiene w t da cui supposta nota R si ricavano L e C:

Calcolo dell'errore

Utilizziamo le derivate parziali per calcolare l'errore:

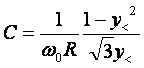
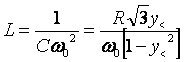
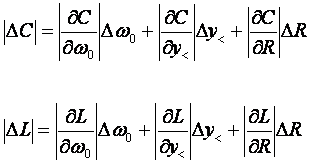
Si considerano nulli gli errori sulla resistenza variabile e quindi il calcolo dell'errore si riduce a:

Modalità di esecuzione

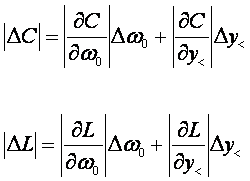
Vediamo ora da più vicino come si posizionano le manopole dell'oscilloscopio e come si ottengono i dati necessari alla risoluzione del problema.

Prima di tutto bisogna settare lo strumento in questo modo :

- Mode  Auto

- Coupling AC

- Source    Vert.

- CH 1 e CH 2  AC ( o DC )

Successivamente si seleziona GRD in entrambi i canali e si tara lo strumento posizionando sullo schermo i segnali coincidenti all'asse dei tempi (in realtà questa posizione non è fissa ma risulta di comodo, specie all'inizio ).

- Si riporta lo strumento nelle condizioni di partenza e si eseguono le misurazioni.

- Si selezionano un valore di L, uno ci C e uno di R. Si valutano:

la frequenza di risonanza per cui i due segnali risultano in fase

la frequenza di dimezzamento, ricordando che esisteranno due frequenze di dimezzamento e che ci serviranno per la determinazione dei valori effettivi di C e L

la variazione di frequenza che corrisponde ad una tacca. Anche in questo caso 

bisognerà provare prima in un senso e poi nell'altro, considerando infine (per esempio) il valore maggiore tra quelli trovati. Questa misura servirà a valutare l'incertezza sui dati ottenuti.

Calcoli per determinare i valori di L, C e dell'errore

Richiamando ora le formule per il calcolo di L e C ed i dati ricavati dall'oscilloscopio procediamo col determinare i valori necessari per l'esperienza:

Dati w

w^I

w^II

Frequenza di dimezzamento y_< y_>

y^I=16.1 y^II=17.8

Range di lavoro=100K

Le precedenti misure si riferiscono tutte al frequenzimetro, quindi vanno tutte misurate in Hz.

Resistenza=990 Ohm

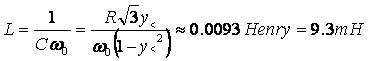
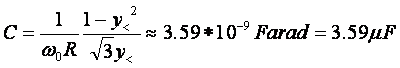
Calcoliamo l'errore attraverso le derivate parziali:

Commenti ed osservazioni.

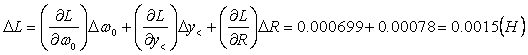
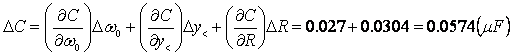
- Per ciò che concerne il frequenzimetro e il generatore di forma d'onda è bene accertarsi prima di iniziare la prova che:

la forma d'onda selezionata sia sinusoidale

l'ordine di grandezza selezionato sia 100K oppure 10K in quanto questo risulta essere il range migliore per l'esecuzione delle misurazioni

l'amplitude del frequenzimetro sia posta in posizione massima

si operi con valori di resistenza alti (990 ohm nel nostro caso)

si consideri inoltre che il valore letto sul frequenzimetro è una frequenza espressa in Hz, per trovare la pulsazione bisogna rifarsi alla relazione: w pf

(Es. se leggiamo sul frequenzimetro 27,5 Hz la nostra pulsazione sarà uguale a 27,5*2*3,14 ).

- Bisognerà poi porre attenzione nell'esprimere i valori dell'induttanza in Henry e quelli della capacità in Farad.

Siccome però un Farad è una capacità molto elevata useremo dei sottomultipli in particolare il mF (nanofarad) mentre al posto dell'Henry useremo i mH (millihenry).

- L'esperienza risulta riuscita in quanto siamo partiti con valori di L pari a 10 mH e C pari a 3,3 mF che abbiamo trovato come verifica alla fine dei nostri conti.

Inoltre per calcolare Dw e Dy_< si può valutare sull'oscilloscopio che l'intervallo Dy_< produce in ampiezza un intervallo DV_R pari ad una tacca dell'asse verticale dell'oscilloscopio nella scala corrente. Quindi risulta possibile minimizzare l'errore amplificando opportunamente la scala verticale prima di effettuare la misura.