MECCANICA STATISTICA QUANTISTICA

ENSEMBLE CANONICO

Per un sistema che possa scambiare con l'ambiente soltanto energia la media di una grandezza a associata ad un sistema di Hamiltoniana H e a contatto con un ambiente a temperatura T è data dalla seguente relazione che definisce la media statistica quantistica della grandezza a

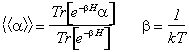
Tale risultato si può giustificare assumendo che il sistema in interazione con l'ambiente evolva nel tempo dall'uno all'altro autostato dell'energia passando in ciascuno stato un eguale tempo t . Dopo un tempo Mt la media temporale di a sarà espressa in termini del numero delle volte m_k   che il sistema ha visitato l'autostato E_k e del valor medio della grandezza a su tale autostato.

L'ipotesi ergodica asserisce che l'insieme degli concide per grandi M con l'insieme dei modi con cui si possono distribuire M oggetti in certi livelli energetici E_k con il vincolo di una energia media fissata. Si ipotizza cioè che ciascuno insieme degli corrisponda ad una possibile evoluzione del sistema. Per tempi abbastanza lunghi la media è praticamente coincidente con quella associata all'insieme degli m_k che si realizza nel maggior numero di modi. Si può infatti pensare di suddividere il tempo di media in n intervalli eguali ognuno dei quali abbastanza lungo perché la media su tale intervallo non dipenda dalla lunghezza dell'intervallo e l'energia media sia costante. Se l'insieme degli ^l caratterizza il moto relativamente all'intervallo l-esimo la media complessiva si esprimerà come media delle medie associate ai singoli intervalli.

In base all'ipotesi ergodica per un numero sufficientemente grande di intervalli si realizzeranno tutti i possibili insiemi   ^l compatibili coi vincoli

La media su tanti intervalli potrà pertanto calcolarsi utilizzando l'insieme degli ^l che si realizza nel maggior numero di modi compatibilmente con i vincoli citati.

Il numero di modi di distribuire m oggetti in un certo numero di stati assegnati (supponiamo per semplicità un numero di livelli energetici limitato k=0,s) si esprime tramite la nota formula

La configurazione che massimizza W col vincolo di un numero di sistemi pari ad m e di un'energia media fissata si ottiene col metodo dei moltiplicatori di Lagrange cercando il massimo della grandezza ausiliaria G

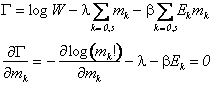
Supponendo che le occupazioni dei livelli associate alle configurazioni prossime al massimo cercato siano tutte molto elevate possiamo usare la formula di Stirling per il logaritmo del fattoriale.

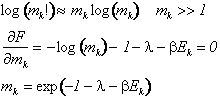
I moltiplicatori di Lagrange sono implicitamente espressi dai vincoli.

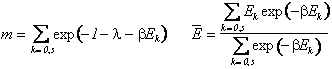
L'energia media si esprime come una media delle possibili energie del sistema ciascuna delle quali pesata per un "numero di occupazione" del livello n_k che dipende dall'interazione con l'ambiente.

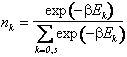
NOTA le considerazioni che abbiamo fatto si basano su di una ipotesi semplificativa sulla evoluzione del sistema fisico,ovvero che tale evoluzione si possa assimilare alle transizioni da uno stato energetico all'altro. Ad esempio nel caso di un sistema a due stati l'evoluzione sarà una oscillazione tra i due stati che noi schematizziamo come una successione di salti tra i due livelli. In generale lo stato del sistema ad un certo istante sarà la sovrapposizione di autostati dell'energia e l'interazione con l'ambiente porterà ad una evoluzione dei coefficienti di tale sovrapposizione.

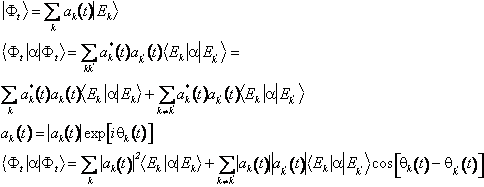
La media temporale interverrà pertanto sia sui termini diagonali che su quelli non diagonali che compaiono nella ( ). L'ipotesi aggiuntiva è che i secondi si medino a zero per tempi sufficientemente lunghi per effetto della dipendenza dalla funzione oscillante coseno. A questo punto l'ipotesi di una evoluzione a salti è una lecita schematizzazione per la valutazione della media temporale della probabilità di osservare il sistema nello stato k.

Riotteniamo la precedente impostazione ponendo

E' utile definire la funzione di partizione Z in termini della quale è possibile esprimere sia i numeri di occupazione che l'energia media.

L'espressione della funzione di partizione si generalizza facilmente notando che la ( ) è il caso particolare della seguente espressione nel caso in cui la traccia viene eseguita sugli autostati dell'energia.

Una ulteriore considerazione ci permette di identificare il parametro b in termini della temperatura assoluta del sistema. Infatti un lavoro infinitesimo operato in una trasformazione quasistatica sul sistema corrisponderà ad una piccola variazione dei livelli energetici dovuta alla interazione con le forze che producono il lavoro senza che venga alterata la distribuzione degli n_k . Otteniamo così una variazione del logaritmo della funzione di partizione

Se dalla ( ) isoliamo il lavoro fatto dal sistema, ricordando che esso è eguale alla variazione dei livelli energetici cambiata di segno, , identifichiamo l'energia interna con l'energia media ed usiamo il primo principio della termodinamica ,otteniamo

Ovvero la relazione che definisce l'entropia in termini della funzione di partizione e dell'Energia interna

Il parametro bT viene fissato pari all'inverso della costante di Boltzmann.

In alternativa all'energia nterna o all'entropia possiamo ricavare l' energia libera.

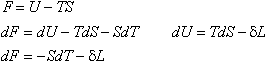
Confrontando con la precedente identificazione del lavoro e dell'entropia otteniamo

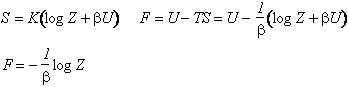
L'energia interna si ottiene direttamente dalla funzione di partizione

Le relazioni che legano l'energia libera,l'energia interna e/o l'entropia alla funzione di partizione sono di fondamentale importanza perché consentono di esprimere grandezze macroscopiche tramite la conoscenza dell'insieme degli autovalori dell'energia.

Tra queste la capacità termica del sistema si definisce come rapporto tra il calore ceduto in una trasformazione in cui il sistema non compie lavoro ed incremento di temperatura .

L'entropia si può mettere in relazione con l' energia libera tramite la ( ).

In alternativa sfruttando la definizione di entropia di ( ) si ottiene

Le derivate parziali che compaiono nella ( ) corrispondono ad incrementi dell'energia libera o della funzione di partizione in cui non viene compiuto lavoro, a derivate cioè in cui rimangono invariati i parametri che nell'Hamiltoniana definiscono l'interazione con l'esterno.

Si noti infine che essendo la funzione di partizione esprimibile tramite una traccia risulta invariante rispetto a trasformazioni canoniche degli stati su cui si opera la traccia o degli operatori che sono argomento della traccia.

Nella ( ) gli n indicavano un insieme completo di stati e l'espressione finale può essere letta come traccia sugli m di un operatore trasformato o come traccia di un operatore su stati trasformati. Questa proprietà consente di utilizzare le trasformazioni canoniche per riportare,quando è possibile, il calcolo della funzione di partizione a quello di un sistema in cui si conoscono gli autovalori dell'Hamiltoniana.

Sistema a due stati a temperatura T Nell'ensemble canonico la funzione di partizione e di conseguenza l'energia libera si esprimono immediatamente tramite gli autovalori dell'Energia.

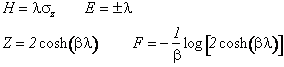
Si noti che sfruttando le operazioni di rotazione si mostra che la funzione di partizione che abbiamo calcolata coincide con quella di un sistema di Hamiltoniana

L'Energia libera si ottiene immediatamente

L'energia interna e la capacità termica del sistema si ottengono dalle ( ) e ( ).

Si noti come l'energia interna e l'energia coincidano nel limite di temperatura nulla in cui si può trascurare l'entropia.

La capacità termica tende a zero sia a bassa temperatura come ci si aspetta dal terzo principio della termodinamica che ad alta temperatura e questo è in contraddizione con la legge di Dulong e Petit dovuta alla natura prettamente quantistica del sistema.

Oscillatore armonico a temperatura T Consideriamo un oscillatore armonico a contatto termico con un ambiente a temperatura T. L'energia libera del sistema si esprime facilmente nell'Ensemble canonico come somma di una serie geometrica di ragion minore di uno.

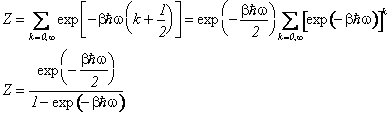
L'energia libera e l'energia interna saranno pertanto

Si verificano facilmente i limiti di bassa temperatura e di alta temperatura. Nel primo caso l'entropia tende a zero e l'energia libera coincide con l'energia dello stato fondamentale dell'oscillatore armonico. nell'altro si verifica il teorema dell'equipartizione classico per l'energia interna.

La capacità termica

Ad alta temperatura si verifica la legge di Dulong e Petit (Capcità termica indipendente dalla temperatura) ed a bassa temperatura un decadimento esponenziale.

ENSEMBLE GRAN CANONICO

Consideriamo il caso in cui il sistema in equilibrio con l'ambiente sia costituito da un numero N di subsistemi identici ciascuno dei quali l autostati di energia e_l . L'Hamiltoniana del sistema si esprimerà in termini degli operatori che danno l'occupazione dei singoli livelli e delle energie di tali livelli.

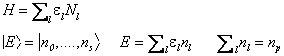
Gli operatori che danno l'occupazione dei livelli sono operatori che commutano tra di loro ed è pertanto possibile definire degli autostati simultanei in cui gli n_l sono gli autovalori degli operatori N_l . La funzone di partizione di tale sistema nell'Ensemble canonico si esprime nella base degli autostati simultanei dei numeri di occupazione come segue.

Nella ( ) compare una somma s-pla estesa a tutti i possibili valori che possono assumere gli n_l compatibilmente col principio di Pauli. Sfruttando l'espressione degli autovalori otteniamo.

Risulta a questo punto evidente la difficoltà di eseguire le somme tenendo conto del vincolo specialmente nel caso di un gran numero di livelli energetici. Si preferisce pertanto introdurre un nuovo Ensemble detto Gran canonico in cui il sistema può scambiare con l'ambiente energia e particelle con il vincolo che il numero medio di particelle sia costante. A tale vincolo è associato un ulteriore moltiplicatore di Lagrange detto potenziale chimico.

Nell'ensemble Gran Canonico la media statistica quantistica si definisce

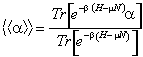
Il calcolo della funzione di partizione si esegue nell'ensemble Gran Canonico è grandemente semplificato per la possibilità di eseguire le somme indipendentemente per ogni livello.

Le funzioni termodinamiche divengono somma delle analoghe grandezze associate ad ogni livello. Ad esempio l'Energia libera;

Se le particelle sono bosoni o fermioni e lo stato energetico non presenta degenerazioni, possiamo esguire le somme. Nel caso dei bosoni ci potremo valere della somma della serie geometrica se la ragione è minore di uno ciò implica una limitazione per il potenziale chimico che dovrà risultare minore del minimo livello energetico.

BOSONI

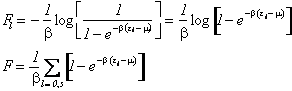
FERMIONI

I numeri di occupazione medi associati ad ogni livello si ottengono derivando rispetto ai livelli energetici l'energia libera.

Si ottiene così una espressione che caratterizza la statistica delle particelle detta rispettivamente statistica di Bose o di Fermi.

Si noti come nel caso di Fermi l'occupazione media sia come deve essere compresa tra zero ed uno mentre nel caso di Bose la limitazione sul potenziale chimico è necessaria per avere una occupazione media maggiore di zero.

Tutte le considerazioni fatte sul gran canonico sono accettabili se le fluttuazioni del numero di particelle sono trascurabili, in tal caso il vincolo debole sul valor medio non differisce apprezzabilmente dal vincolo forte sul numero di particelle. Si può far vedere come tale condizione sia soddisfatta per un numero grande di particelle. Si noti infine come le nostre considerazioni si basino sulla possibilità di esprimere l'Hamiltoniana del sistema come somma di termini indipendenti (corrispondenti cioè ad operatori che commutano). A tale espressione dell'Hamiltoniana si può pervenire tramite una trasformazione canonica dell'Hamiltoniana originale. Le "particelle" in tal caso saranno associate ai nuovi gradi di libertà indipendenti definiti dalla trasformazione. Ad esempio per le particelle itineranti su di un reticolo l'Hamiltoniana si trasforma in forma diagonale passando al reticolo reciproco in questo caso dobbiamo considerare i modi del reticolo reciproco e l'occupazione ad essi assaciata.