L'Ampiezza di probabilità e l'Equazione di Schrödinger

Il coefficiente a (in generale complesso e funzione del tempo) si determina dalla cosiddetta condizione di normalizzazione

Se y₊(x,t) e y_-(x,t) sono a loro volta normalizzate otteniamo una condizione per il modulo quadro di a

Che solo y₊(x,t) e y_-(x,t) intervengano nella espressione dello stato è conseguenza del fatto che se si osserva da che parte è passata la particella otteniamo uno tra due possibili risultati corrispondenti a y₊(x,t) o y_-(x,t).

Ci proponiamo di determinare la legge di evoluzione temporale della y(x,t).

DIFFUSIONE CLASSICA

Come preliminare determiniamo una legge di evoluzione della densita' di probabilità nota come legge di diffusione.

Consideriamo ome primo esempio una passeggiata casuale in cui il punto mobile si trovi nell'origine al tempo iniziale e compia un spostamento verso destra o verso sinistra nell'intervallo di tempo t a seconda se nel lancio di una monetina e' uscita testa o croce. la registrazione della posizione del punto in corrispondenza degli istanti di tempo selezionati rappresenta una traiettoria o realizzazione del processo stocastico. L'insieme delle traiettorie è detto ensemble delle realizzazioni. Possiamo definire medie temporali su ciascuna realizzazione e medie d'ensemble ad un certo istante. Per un ensemble sufficientemente grande (contenente cioe' un gran numero di realizzazioni) le medie di ensemble saranno di poco differenti dalle medie calcolate con la probabilità P(i,n)di osservare il punto mobile in una certa posizione ia ad un certo istante nt. Tale grandezza si determina risolvendo una semplice legge di evoluzione in avanti

(3)

Tale legge è una diretta conseguenza delle leggi classiche di composizione della probabilita': la particella si trova in x=ia al tempo t=(n+1)t solo e solo se si trovava in x=(i-1)a al tempo t=nt ed è uscita croce o x=(i+1)a al tempo t=nt ed è uscita croce. E' facile rendersi conto che con tale legge di evoluzione la probabilita' di osservare la particella lontano dall'origine cresce nel tempo. L'evoluzione è irreversibile. Se infatti vogliamo determinare l'evoluzione all'indietro nel tempo ci chiediamo cioè quale configurazione della P(i,n) è compatibile con una nota configurazione della P(i,n+1) otteniamo la stessa configurazione che si aveva nell'evoluzione in avanti al tempo n+2. Invertendo il tempo non si possono ripercorrere le stese configurazioni. Per l'evoluzione all'indietro vale l'equazione alternativa.

(4)

Si noti che a destra i fattori 1/2 che si riferivano precedentemente alle probabilità condizionate di abbandonare una certa posizione compiendo un passo a destra o a sinistra si associano ora alle probabilità condizionate di pervenire in una certa posizione compiendo un passo a destra o a sinistra.

Per introdurre il limite in cui sia l'ampiezza del passo che l'intervallo temporale tendano a zero occorre rendere piccola la variazione della densita' di probabilita' ad ogni passo Cio' si ottiene modificando la passeggiata casuale come segue. Il punto mobile si diparte dall'origine ed evolve secondo la seguente legge probabilistica nel piccolo intervallo temporale t il punto materiale si sposta con probababilita' (l/2)t di Dx verso destra o verso sinistra e con probababilita' !-lt rimane fermo. Applicando le leggi classiche di composizione della probababilita' otteniamo la seguente equazione per l'evoluzione in"avanti" nel tempo della densità di probabilità. Per evoluzione in avanti intendiamo che la densità di probabilità al tempo t+t è determinata dalla densità di probabilità al tempo precedente t.

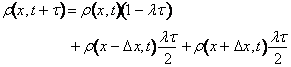(5)

Il primo termine a destra nell'Eq. (5) rappresenta la probabilità che il punto, presente nell'intorno di x al tempo t, non si sia mosso nel tempo t il secondo ed il terzo rappresentano le probabilita' che il punto a distanza Dx da x al tempo precedente, abbia raggiunto l'intorno di x al tempo t. Si sommano i vari termini in quanto corrispondenti a tutti gli eventi mutuamente esclusivi che portano ad osservare il punto mobile nel'intorno di x al tempo t.

Per ottenere l'Eq. di diffusione sviluppiamo le densità di probabilità in Dx portando lo sviluppo fino al secondo ordine.

(6)

Sostituendo nella (5) otteniamo

(7)

Dividendo per t , nel limite di t piccolo, con il coefficiente di diffusione definito come segue, si ottiene l'Eq. di diffusione per la densità di probabilità

(8)

(9)

Si noti come la derivata prima rispetto al tempo implichi una evoluzione irreversibile.

Analoghe considerazioni ci portano alla Equazione di evoluzione della densità di probabilità all'"indietro" nel tempo.

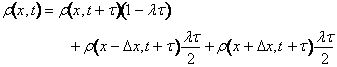(10)

Il primo termine a destra nell'Eq. (10) rappresenta la probabilità che il punto, sia presente nell'intorno di x al tempo t+t, in quanto non si è mosso nel tempo t ,il secondo ed il terzo rappresentano le probabilità che il punto si trovi a distanza Dx da x al tempo t+t, provenendo dall'intorno di x al tempo t. Ripetendo le considerazioni fatte per l'evoluzione in avanti otteniamo l'Equazione di diffusione per l'evoluzione all'indietro.

(11)

I momenti definiti come

(12)

soddisfano delle semplici equazioni ricorrenti che si ottengono dalla Eq. di diffusione con un procedimento di integrazione per parti

(13)

Il doppio segno si riferisce all'evoluzione in avanti (+) o all'indietro (­). Si noti come il momento d'ordine zero altri non sia che l'integrale di normalizzazione che è ovviamente costante, il momento d'ordine uno costante nel tempo esprime il fatto che nel moto di diffusione la particella si muove con eguale probabilità verso destra e verso sinistra. Il momento d'ordine due esprime, nel caso di primo momento nullo, l'incertezza sulla posizione del punto. Integrando nel tempo la (13) si ha rispettivamente per l'evoluzione in avanti o all'indietro.

(14)

Si noti che la costante di integrazione è stata determinata in termini dell'incertezza all'istante iniziale per l'evoluzione in avanti ed in termini dell'incertezza ad un tempo finale T per l'evoluzione all'indietro. L'irreversibità si manifesta chiaramente quando si rileva che non è possibile scegliere le costanti in modo da far coincidere a tempi intermedi le incertezze associate ai due tipi di evoluzione.

Una soluzione particolarmente semplice dell'equazione di diffusione si esprime come una gaussiana centrata sull'origine con varianza che varia nel tempo con la legge del momento del secondo ordine

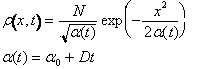(15)

Questa soluzione è ovviamente compatibile con una densità di probabilità iniziale gaussiana.

(16)

E' facile vedere che in tal caso il valor medio della posizione coincide con il valore più probabile x=0 e l'incertezza coincide con s L'evoluzione in avanti mantiene la forma gaussiana con un'incertezza che aumenta nel tempo con la legge del momento del secondo ordine.

(17)

Analogamente per l'evoluzione all'indietro se al tempo finale T abbiamo

(18)

per tempi t minori di T si ottiene

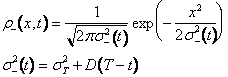(19)

Per ottenere la legge di evoluzione dell'ampiezza di probabilità è naturale tentare una generalizzazione della equazione di diffusione. Ciò sarebbe coerente con la regola euristica di applicare le leggi valide per la probabilità alle ampiezze di probabilità.

L'irreversibilità costituisce una difficoltà. Ci si aspetta infatti che la meccanica classica dia previsioni equivalenti a quelle della meccanica quantistica almeno nell'ambito dei fenomeni macroscopici e pertanto una proprietà qualitativa quale quella della reversibilità temporale delle equazioni di evoluzione delle grandezze osservabili deve valere,come in meccanica classica, anche in meccanica quantistica.

La grandezza osservabile è peraltro la densità di probabilità

(20)

Se consideriamo il caso particolare di una ampiezza di probabilità reale al tempo t=0 possiamo ottenere una evoluzione reversibile se scambiando t in -t scambiamo anche y con y

(21)

La seconda è compatibile con l'Equazione di diffusione se il coefficiente di diffusione è puramente immaginario se si sostituisce cioè D con iD nell'equazione di diffusione per le ampiezze di probabilità. Il confronto con una serie di proprietà sperimentali porta ad identificare il coefficiente di diffusione in termini della costante di Planck e della massa della particella ottenendo cosi l'equazione di diffusione nella forma finale nota come Equazione di Scrodinger per la particella libera.

(22)

L'Equazione di Scrödinger per la particella libera si presta ad una serie di applicazioni che ne illustrano la potenzialità.

EVOLUZIONE DELLA DENSITA' DI PROBABILITA' ED EQUAZIONE DI CONTINUITA'

L'ampiezza di probabilità è una grandeza complessa ed è pertanto sempre possibile esprimerla in termini di due funzioni reali associate rispettivamente al modulo ed alla fase.

(23)

Il modulo A è la radice quadrata della densità di probabilità. Per interpretare la fase S conviene ricavare dalla Eq. di Scrodinger una Eq. di evoluzione per la densità di probabilità. Mediante i seguenti passaggi

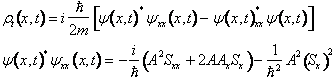(24)

otteniamo l'eq. desiderata.

(25)

Questa è la versione unidimensionale di una Eq. di continuità. L'evoluzione della densità di probabilità è determinata ad ogni istante dalla divergenza di una corrente. Tale corrente è data dal prodotto della densità di probabilità per un campo di velocità che si ottiene come gradiente della fase S cambiato di segno e diviso per la massa m.

Possiamo pensare che lo stato quantistico di una particella sia assimilabile ad un modello di fluido il cui stato è definito in ogni punto dello spazio da una densità di particelle (intesa come numero di particelle nell'intorno del punto diviso il numero di particelle totali) pari alla densità di probabilità ed una velocità proporzionale al gradiente della fase.

Si noti la differenza qualitativa con l'Eq di diffusione della densità di probabilità classica in cui l'evoluzione è determinata dalla sola densità di probabilità ai tempi precedenti.

EVOLUZIONE DELLA FASE

Analogamente si può determinare l'evoluzione della fase. Dall'Eq. di Scrodinger ricaviamo

(26)

da cui è immediato ricavare l'eq. desiderata

(27)

Nell'evoluzione della fase distinguiamo una parte "classica" associata al campo di velocità agli istanti precedenti e da una parte quantistica associata alla variazione nello spazio dell'ampiezza.

In presenza di un campo di forze esterno l'Eq(di evoluzione della fase si generalizza come segue

(28)

Nel caso particolare di una energia potenziale quadratica(oscillatore armonico di pulsazione w

(29)

STATI QUASI-CLASSICI

E' possibile ricavare una soluzione della equazione di continuità e dell'equazione di evoluzione della fase con densità di probabilità gaussiana di ampiezza cstante nel tempo pari ad s =h/(4mpw) e centrata su di un valore più probabile x=g(t) dato da una funzione del tempo da determinare ed una fase sotto forma di un di polinomio in x con coefficienti dipendenti dal tempo. La particolare scelta della varianza della gaussiana comporta una cancellazione dei termini quadratici in x a secondo membro della ( ). Possiamo quindi limitarci a condiderare per S un polinomio del primo ordine in x

(30)

Sostituendo nell'Eq. di evoluzione ed eguagliando termini dello stesso ordine in x otteniamo.

(31)

Dalla Eq. di continuità otteniamo

(32)

Si possono riconoscere nelle (31b,32 ) le equazioni del moto classico ove g(t) ed f(t) sono rispettivamente le leggi orarie associate alla posizione dell'oscillatore ed alla quantità di moto .

(33)

Nella (31a) riconosciamo la differenza tra l'energia cinetica e l'energia potenziale associata al moto classico Tale grandezza è detta Lagrangiana associata al moto classico ed il suo integrale tra due tempi definti è detto Azione classica.

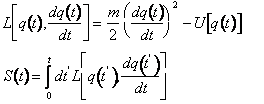
In generale si può definire una Lagrangiana e quindi una azione per una qualsiasi funzione del tempo q(t)

(34)

Da queste relazioni si evince che l'azione dipende dalla particolare funzione del tempo q(t). Parliamo di Azione classica se scegliamo come funzione del tempo la legge oraria classica.

(35)

Si ottiene quindi

(36)

Abbiamo ottenuto un particolare stato dell'oscillatore armonico in cui: la densità di probabilità è una gaussiana di varianza costante nel tempo, centrata ad ogni istante sulla posizione dell'oscillatore armonico classico. Il campo di velocità e' costante nello spazio e variabile nel tempo come la velocità dell'oscillatore armonico classico. L'oscillazione temporale e' determinata dalla Azione classica incrementata di una quantità corrispondente all'energia che rimane nell'oscillatore se lo stato classico è quello di quiete.

. Questo stato è detto "quasi-classico" per la caratteristica di avere una incertezza indipendente dal tempo e dall'ampiezza dell'oscillazione .

Converrà accennare che il concetto di Azione è alla base della cosiddetta formulazione variazionale della meccanica classica per cui fissati due istanti di tempo e due posizioni A,B nello spazio una particella che si muove in un campo di forze conservativo da A a B segue il percorso corrispondente alla legge oraria che rende minima l'Azione.( Principio di minima azione o di Mapertuis)

In meccanica quantistica si può far vedere che ad ogni percorso che unisce A e B corrisponde una ampiezza di probabilità diversa da zero e che al percorso "classico" corrisponde l' ampiezza di probabilità massima.

.

DIFFUSIONE QUANTISTICA.

Al tempo t=0 supponiamo che lo stato della particella sia associato ad una ampiezza di probabilità reale pari alla radice quadrata di una gaussiana.

(37)

In questa ipotesi la densità di probabilità coincide al tempo iniziale con quella considerata per la diffusione "classica" del paragrafo precedente.

A parte la normalizzazione si tratta ancora di una gaussiana ed e' pertanto compatibile con la soluzione gaussiana dell'Equazione di diffusione di (22) in cui D e' sostituito da iD.

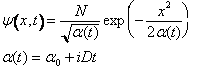(37)

L'identificazione con lo stato assegnato al tempo iniziale impone che

(39)

La densità di probabilità al tempo t risulta essere

(40)

Si ottiene pertanto che la densità di probabilità è ancora una gaussiana di varianza

(41)

Ci sono due fondamentali differenze rispetto alla diffusione classica.La prima è la dipendenza dal quadrato del tempo. Tale dipendenza è associata alla reversibilità temporale della evoluzione. La seconda è la dipendenza della rapidità con cui aumenta l'incertezza della posizione dalla incertezza iniziale (diffusione). Minore è tale incertezza più rapida è la diffusione quantistica.

Dal punto di vista del modello di fluido introdotto nel paragrafo precedente si osservi che il fluido è,nelle nostre ipotesi, in quiete al tempo iniziale (fase nulla identicamente nulla e pertanto campo di velocità nullo) e si pone in moto successivamente. Il campo di velocità associato è infatti

(42)

STATI STAZIONARI PER UNA PARTICELLA VINCOLATA SU DI UN SEGMENTO

Definiamo stati stazionari quegli stati a cui corrisonde una densita' di probabilita' indipendente dal tempo.

Gli stati stazionari si possono realizzare con ampiezze di probabilita' in cui la dipendenza dal tempo si riduca ad un fattore di fase

(43)

Sostituendo nella Eq. di evoluzione si ottiene la seguente equazione differenziale ordinaria per l'ampiezza indipendente dal tempo.

(44)

La (44) e' detta Equazione di Schrödinger indipendente dal tempo.

Il vincolo esige che la particella abbia probabilità nulla di trovarsi a qualsiasi istante in x negativo o nullo e in x maggiore o eguale ad L. Dobbiamo pertanto imporre alla soluzione di (44) questa particolare condizione al contorno. Ponendo

(45)

riconosciamo l'equazione di un oscillatore armonico in cui il tempo è sostituito dalla posizione x. Conviene esprimere la soluzione generale come

(46)

Le condizioni al contorno sono soddisfatte se

(47)

La seconda implica la quantizzazione del parametro E ovvero l'energia E (tali sono infatti le dimensioni di E) può assumere solo i valori

(48)

Le corrispondenti ampiezze normalizzate risultano pertanto

(49)

Questo semplice esempio ci mostra la possibilita' di associare alle soluzioni stazionarie un parametro quantizzato con le dimensioni di un'energia. Vedremo in seguito che tale parametro e' effettivamente l'energia quantizzata presente nei diversi fenomeni citati nell'introduzione.

LA DIFFRAZIONE DA DUE FENDITURE

Se nell'esperimento di diffrazione da due fenditure consideriamo alternativamente solo una delle due fenditure aperta lo stato della particella all'istante in cui emerge si può modellare con una ampiezza di probabilità pari alla radice quadrata di una gaussiana centrata rispettivamente in x=a o in x=-a e di varianza pari alla larghezza d delle fenditure. La densità gaussiana non è forse una scelta particolarmente adatta per l'esistenza di code che si estendono all'infinito ma il peso di tali code è in realtà trascurabile se la varianza della gaussiana è molto minore della distanza tra le fenditure.

(50)

Nel caso in cui ambedue le fenditure sono aperte lo stato della particella si ottiene come combinazione lineare con peso eguale delle ampiezze appena introdotte.

(51)

Il peso è determinato dalla condizione di normalizzazione

(52)

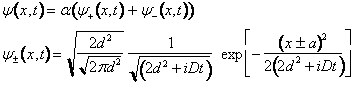
Si noti che se la sovrapposizione delle due ampiezze di probabilità è trascurabile il modulo quadro del peso è 1/2. In altre parole al tempo iniziale la densità di probabilità soddisfa la regola classica a meno di una correzione trascurabile che trae origine dall'avere usato delle funzioni che si estendono all'infinito. Ciò corrisponde ad affermare che su di una lastra fotografica posta a contatto diretto con la superfice dell'interferometro non si deve rivelare una figura di diffrazione. Nell'esperimento infatti la lastra è posta ad una certa distanza grande rispetto sia alle dimensioni tipiche dell'interferometro. Nel tempo necessario alla particella per raggiungere la lastra l'ampiezza di probabilità definita sul piano ortogonale al moto evolverà secondo l'equazione di Scrödinger .

(53)

La densità di probabilità si puo' esprimere come segue

(54)

L'evoluzione temporale è mostrata in figura.