|
|
| |
Gas perfetto, quasi perfetto, reale
Il gas perfetto è il più semplice fluido operante in termodinamica.
Si definisce perfetto un gas non viscoso che soddisfa ad
una equazione di stato
pv = RT
dove R è una costante, diversa per ogni specie molecolare.
Per un gas perfetto le capacità termiche massiche (o calori specifici) a pressione e a volume costante (cp e cv) non dipendono nè dalla pressione nè dalla temperatura
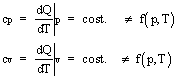
Capacità termica massica
![]()
dove:
Q = calore complessivamente fornito al sistema;
m =
T = temperatura assoluta.
Con riferimento all'u 525h77f nità di
![]()
Per un gas perfetto dQw=0 , dQ=dQe.
Dall'equazione
dQ = dU + p dv
Consideriamo una trasformazione a volume costante (isocora):
![]()
da cui:
dU = cv dT
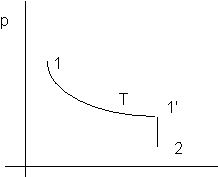
Figura 2. 1
Nota: il tratto 1-1'è a temperatura costante; siccome per i gas perfetti U = U(T) segue che dU per il tratto 1-1'è zero.
U è una funzione di stato e pertanto il risultato ha validità generale, indipendemente dal modo in cui è stato ottenuto.
dQ = dU + p dv = dU + p dv + v dp - v dp = di - v dp
quindi:
![]()
da cui: di = cp dT
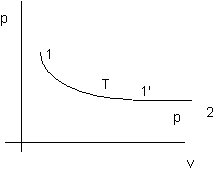
Figura 2. 2
Nota: siccome di = d(U + p dv) = dU + RdT = (cv + R)dT quindi di lungo la trasformazione 1-1'è nulla.
Dalle relazini scritte risulta:
dQ = dU + RdT - v dp
quindi:
dQp=cost = dU + RdT
ricordando:
cp dT = cv dT + RdT
si ottiene:
cp = R + cv R = cp - cv
Un gas quasi perfetto è un fluido che soddisfa all'equazione dei gas perfetti, ma con:
cp = f(T) e cv = f(T)
Un gas reale è viscoso e soddisfa ad un'equazione di stato del tipo:
![]()
con R = cost. e Z = fattore di comprimibilità. Si ha che Z = 1 per un gas perfetto o "quasi". La deviazione di Z dall'unità è dovuta principalmente ai due effetti seguenti:
a) basse temperature, alte pressioni forze intermolecolari importanti;
b) alte temperature, basse pressioni processi di ionizzazione e dissociazione.
Per le nostre applicazioni considereremo, con ottima approssimazione, il gas come perfetto o "quasi perfetto" per quanto riguarda le proprietà termodinamiche.
Per un gas perfetto vale la relazione:
p Vmol = R0T (2.1)
dove R0 = 8310 J/KgmolK e Vmol = V/n (volume di 1 Kgmol) con n = massa misurata in Kgmol e V = volume occuparo dalla massa n.
Quindi la (2.1) può essere riscritta come segue: pV = nR0T
indicando con m la stessa massa n, però misurata in Kg e con mmol il numero di massa molecolare definito dal fattore di conversione:
1 Kgmol = mmol Kg
si ottiene:
n/m = 1 Kgmol/mmol Kg = 1
(è la stessa massa misurata in due diverse unità di misura) che sostituita dà:
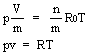
L'equazione di stato, con riferimento a m, si scrive anche: pV = mRT
Per questi gas vale la relazione:
pv = RT
|
Trasformazione |
Caratteristiche |
esponente m |
capacità c |
|
isobara |
p=cost T/v=cost |
m=0 |
c=cp |
|
isocora |
v=cost T/p=cost |
|
c=cv |
|
isoterma |
T=cost pv=cost |
m=1 |
|
|
isoentropica (adiabatica reversiblie) |
dQe = 0 dS = 0 pvk = cost |
m=k= |
c=0 |
|
politropica |
c=cost pvm=cost |
m |
c=cost |
tabella 2.1
Determiniamo l'equazione della isoentropica; partiamo da:
dQ = dU + pdv
essendo isoentropica dS = 0 dQ = 0, quindi:
dU + p dv = 0
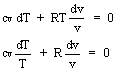
![]()
ponendo cp/cv = k:
![]()
da cui integrando:
ln T + ln vk-1 = cost
ln T vk-1 = cost
T vk-1 = cost
ricordando che, dall'equazione di stato dei gas perfetti:
![]()
segue:
pvk = cost
c.v.d.
Vediamo ora l'equazione della politropica:
![]()
![]()
![]()
da cui ponendo:
![]()
si ottiene:
(Tv)m-1 = cost
(pv)m = cost
Rappresentiamo le trasformazioni dei gas perfetti nel diagramma di Clapeyron:
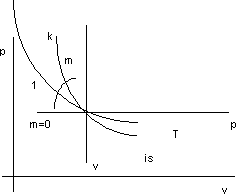
Figura 2. 3
Per il criterio lagrangiano vale, con riferimento alla figura 2.4:
dQ = dU + pdv
![]()
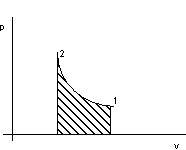
Figura 2. 4
Per il criterio euleriano vale, com riferimento alla figura 2.5:
![]()
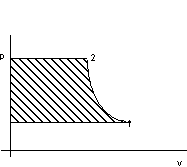
Figura 2. 5
Il diagramma di Clapeyron non dà alcuna informazione in merito ai calori scambiati nel caso di trasformazioni.
Il diagramma entropico nasce dall'esigenza di rappresentare graficamente i calori scambiati nel corso delle trasformazioni. Sull'asse delle ordinate è riportata la temperatura assoluta T, mentre sulle ascisse si ha la funzione di stato S entropia, in quanto:
![]()
e le aree sottese dalle curve rappresentative dell'entropia misurano il calore scambiato.
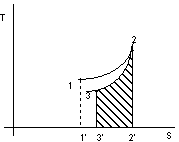
Figura 2. 6
Con riferimento alla figura 2.6:
![]() calore
fornito durante la trasformazione 1-2
calore
fornito durante la trasformazione 1-2
area 1'123
![]() calore
sottratto durante la trasformazione 2-3
calore
sottratto durante la trasformazione 2-3
area 3'322'
Trasformazioni dei gas perfetti.
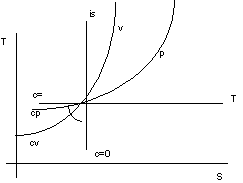
Figura 2. 7
Proprietà del diagramma T-S
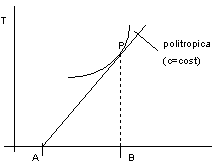
Figura 2. 8
Nella figura 2.8 la curva rappresenta una politropica (c = cost), mentre la retta è la sottotangente alla trasformazione nel punto P.
Con riferimento alla figura 2.8:
![]()
Dal II principio:
cdT = dQ = TdS
![]()
e quindi:
AB = c capacità termica della trasformazione
Vediamo un'altra proprietà del diagramma T-S.
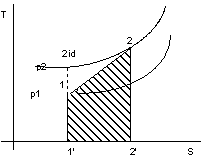
Figura 2. 9
In figura 2.9 la trasformazione 1-2id è adiabatica reversibile, mentre la trasformazione 1-2è adiabatica irreversibile.
Con riferimento alla figura 2.9 si rappresenta la trasformazione irreversibile con la poli- tropica che passa per gli stati iniziale e finale del fluido.
TdS = dQe + dLw
Ma essendo adiabatica dQe = 0, quindi:
dLw > 0 dS > 0
area 11'22'=![]()
Cicli reversibili e rappresentazione nei diagrammi termodinamici

figura 2.10
Con riferimento alla figura 2.10 consideriamo il ciclo percorso in senso orario - reversibile:
-dL = -pdv + dEc + dLw
![]() = area A0ACC0
+ area CBA0C0
= area A0ACC0
+ area CBA0C0
>0 <0
Dal grafico otteniamo che il lavoro L risulta uguale all'area del ciclo.
Il ciclo percorso in senso orario nel diagramma p,v è un ciclo motore (il fluido fa lavoro sull'esterno a spese della sua energia). Si dice che è un ciclo termodinamico diretto. Infatti per il ciclo percorso in senso antiorario:

figura 2.11
![]() = area A0ACC0
+ area C0CBA0 <
0
= area A0ACC0
+ area C0CBA0 <
0
>0 <0
L = Qe < 0 ciclo operatore
Vediamo asesso le rappresentazioni sul diagramma entropico:
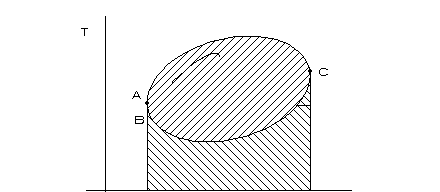
figura 2.11
Conriferimento alla figura 2.11 consideriamo il ciclo percorso in senso orario - reversibile:
TdS = dQe + dLw
Essendo dLw = 0:
![]() = area A0ACC0 + area C0CBA0
= area A0ACC0 + area C0CBA0
>0 <0
Qe = area ciclo = Q1 - Q2
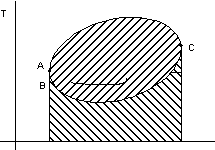
figura 2.13
![]() = A0ACC0 + C0CBA0
< 0 ciclo operatore
= A0ACC0 + C0CBA0
< 0 ciclo operatore
>0 <0
Consideriamo un sistema costituito da acqua (un approccio analogo può essere seguito per altre sostanze).
Forniamo calore a pressione costante: nel fluido si ottiene un aumento di temperatura fino ad un certo limite.
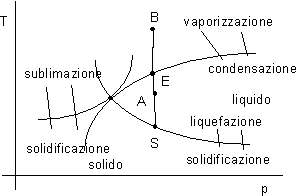
figura 2.14
Nel punto E una ulteriore somministrazione di calore a pressione costante non corrisponde più ad un aumento di temperatura.
Continuando con la somministrazione di calore ad un certo punto si nota un aumento di temperatura (punto B).
Variando la pressione si ottiene una curva luogo dei punti E. Al di sotto di una certa pressione non si troverà più la fase liquida ed è possibile il passaggio tra la fase solida e aeriforme.
Se sottraiamo calore, partendo da A, a pressione costante, si arriva al punto S con solidificazione del liquido a temperatura costante.
Il punto T prende il nome di punto triplo dell'acqua e deve il suo nome al fatto che in quello stato coesistono le tre fasi liquido, solido e aeriforme.
Nel punto triplo è definito una determinata pressione e temperatura, mentre non è determinato il volume massico v.
Il limite nelle considerazioni che si deducono da una rappresentazione di questo tipo è dovuto al fatto che i punti che corrispondono ai passaggi di stato mettono in relazione biunivoca pressione e temperatura e, conseguentemente, non permettono di identificare lo stato del sistema (pressione e temperatura non sono indipendenti).
Ad es . in E si fornisce calore con cambiamento di stato, che però non è individuabile dal diagramma.
Consideriamo il diagramma di Clapeyron:
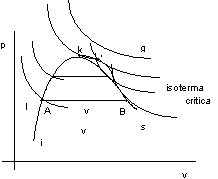
figura 2.15
i = curva limite inferiore;
s = curva limite superiore;
vs = vapor saturo: vapore in equilibrio con il suo liquido;
vsurris = vapore surriscaldato: non è in presenza del suo liquido;
g = gas (a destra dell'isoterma critica);
l = liquido.
Mettiemoci in condizione di effettuare delle isoterme facendo variare pressione e volume. Si hanno le curve delle isoterme sperimentali.
Aumentando le temperatura si ottiene il punto K, detto punto critico, e l'isoterma critica è quella che gli corrisponde.
Per l'acqua il punto critico è definito da:
Tcr = 374 °C
K pcr = 221,3 bar
v = 0,0031 m3/Kg
Per temperature T > Tcr l'andamento dell'isoterma è quello tipico dei gas perfetti.
Il gas compresso isotermicamente non diventa mai liquido cosa non vera per il vapore (T < Tcr).
Titolo del vapore
Nel caso di una miscela di liquido e vapore si definisce come titolo del vapore il rappprto tra la massa di vapore contenuta in una massa totale liquido + vapore e la massa totale suddetta.
in A titolo del vapore x = 0
in B " " " x = 1
In uno stato intermedio il volume massico è dato da:
v = vi(1 - x) + vs x
possiamo dire che il volume massico è composto da due contributi, uno del liquido e uno del vapore, che noi consideriamo distinti (mentre in realtà non lo sono).
vs = volume massico di vapore saturo secco;
vi = volume massico del liquido in condizione di incipiente vaporizzazione.
Il titolo del vapore può essere determinato dal rapporto:
![]()
che corrisponde ad un rapporto tra segmenti AC e AB (vedi figura 2.16).
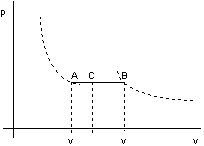
figura 2.16
Calore di vaporizzazione: è la quantità di calore che bisogna fornire, ad una data temperatura, al liquido saturo per trasformarlo completamente in vapore saturo secco.
La quantità di calore che occorre fornire varia al variare della temperatura.
Analoga definizione vale per il calore di condensazione.
Consideriamo un ciclo di carnot infinitesimo tral a temperatura T e T - dT:
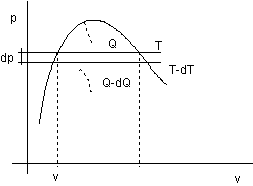
figura 2.17
Con riferimento alla figura 2.17:
![]()
![]()
![]()
Il calore di vaporizzazione r compare lungo la trasformazione isoterma alla temperatura superiore T e coincide con Q:
![]() (2.1)
(2.1)
Per valutare dQ consideriamo che, nel caso di un ciclo reversibile, sul diagramma p v l'area
del ciclo corrisponde al lavoro del ciclo.
Nel nostro caso il lavoro del ciclo corrisponde a Q1 - Q2 dQ per il ciclo infinitesimo (infinitesimo in quanto esteso ad un ciclo infinitesimo).
dL = dQ
l'area del ciclo infinitesimo è data dal prodotto:
![]()
dp (vs - vi) (2.2)
C'è una corrispondenza biunivoca tra temperatura e pressione, per cui ad una variazione infinitesima di temperatura corrisponde una variazione infinitesima di pressione.
Si determina quindi sostituendo (2.2) in (2.1):
![]()
che è la formula di Clapeyron; per il punto critico vs = vi, dp/dT finita, r = 0.
Vogliamo ora descrivere la situazione vista nel diagramma p,v nel diagramma termodinamico T,S.
Dal II principio si ha:
dS = ![]() ( dQ = dQe
+ dLw)
( dQ = dQe
+ dLw)
posso esprimere dQ = ci dT, con ci la capacità termica massica, lungo la curva limite inferiore, che compete ad un certo dT.
Dall'andamento sperimentale di ci in funzione di T (non riportato) si determina il seguente diagramma per la curva limite inferiore:
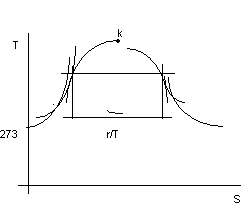
figura 2.18
Usualmente si assegna il valore zero all' entropia corrispondente alla temperatura di 0 °C sulla curva limite inferiore.
Per la curva limite superiore posso definire una capacità termica massica cs e operare in maniera analoga ottenendo la curva limite superiore.
![]()
![]()
![]()
Consideriamo ora il diagramma di Mollier i,S che riporta le entalpie in funzione delle entropie.Nel caso dei vapori non c'è più una semplice proporzionalità tra entalpia e temperatura come avviene per i gas perfetti.
di = dU + p dv + vdp = dQ + v dp = TdS + v dp
Per costruire la curva limite occorre avere a disposizione i due diagrammi p,v e T,s:
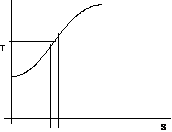
figura 2.19
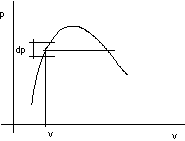
figura 2.20
per la curva limite inferiore considero un intervallo ds in corrispondenza al quale posso determinare Ti.
Per l' isoterma Ti nel p,v considero il dT corrispondente a ds determinando il dp che gli compete: di = Tids + vidp
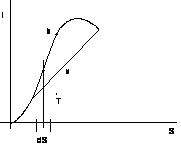
figura 2.21
Per una trasformazione isobara:
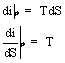
tra le curve limite le trasformazioni isobare sono anche isoterme per cui l'inclinazione delle isobare - isoterme è costante per ogni T.
Si hanno cioè delle rette a pendenza variabile con tangente crescente con la temperatura.
Il punto che corrisponde alla condizione critica è il punto a cui corrisponde la pendenza massima lungo la curva inferiore:
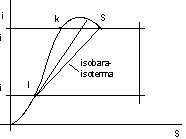
figura 2.22

figura 2.23
v dp non dà contributo lungo la Is perchè isobara - isoterma.
Per passare da I S:
![]()
Il punto S si determina, nota la curva limite inferiore ed il calore di evaporazione, dalla entalpia data da iS = iI + r e dalla retta passante per I di percorrenza di/dS = T (essendo la IS isoterma - isobara).
Consideriamo le figure 2.24 e 2.25:
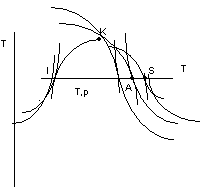
figura 2.24
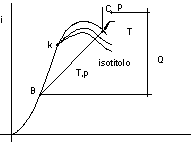
figura 2.25
Linee isotitolo: luogo dei punti che corrispondono a stati con lo stesso titolo (corrispondono alla suddivisione del segmento IS in modo che il rapporto AI rispetto al segmento IS sia costante).
Le isobare nella zona del liquido si confondono con la curva limite inferiore (T,S;i,S).
Nella zona del vapore si ha una uscita con tangente in comune alla isobara - isoterma, dovuta alla relazione:
![]()
Nelle isoterme lontano dalle curve limiti (vapore surriscaldato o fortemente surriscaldato) l'andamento è quello delle isoentalpiche.
Nel diagramma di Mollier se il calore è fornito a pressione costante è possibile individuarlo come un segmento verticale, che corrisponde agli estremi di entalpia:
di = dQ + v dp
Ma essendo p = cost. vdp = 0, quindi:
![]()
QBC = iC - iB
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI paolopaolo-8172 Già nella prima frase c'è un errore: un gas perfetto ha una viscosità, è un fluido ideale quello con viscosità nulla |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026