|
|
| |
Studiamo il moto di un fluido attraverso un condotto avente una certa forma.
Vogliamo determinare la conformazione dei condotti e le condizioni operative necessarie per ottenere che il fluido, mentre scambia lavoro 656c23g ed eventualmente calore, subisca determinate trasformazioni.
Analogamente vogliamo determinare quali trasformazioni subisce un fluido quando attraversa un condotto di forma assegnata e in determinate condizioni.
Supponiamo di voler far espandere un fluido comprimibile, inizialmente in quiete, dalle condizioni uniformi p1, v1, T1, fino alla condizione p2<p1, e di voler disporre dell'energia cinetica conseguente alla diminuzione di pressione.
Ipotesi: il flusso è adiabatico, isoentropico e stazionario.
Definiamo velocità del suono la velocità con cui si propagano nel fluido in quiete le piccole perturbazioni. Abbiamo la seguente relazione:
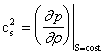
per un gas perfetto che subisce una trasformazione isoentropica vale la seguente relazione:
![]()
applicando il logaritmo naturale a entrambi i membri:
![]() derivando:
derivando:
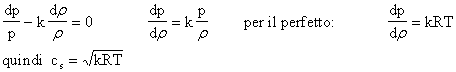
Quest'ultima relazione è vera anche per il vapore, considerando un opportuno valore di k.
Le proprietà di ristagno o proprietà totali di una corrente fluida in moto permanente sono i valori che le proprietà della corrente acquisterebbero se la corrente fosse decelerata adiabaticamente, isoentropicamente e senza scambiare lavoro 656c23g , fino a velocità nulla.
Scriviamo la legge di conservazione dell'energia in forma euleriana per questa decelerazione:
![]()
Qe=0 perché la decelerazione è adiabatica
Li=0 perché il fluido non fa lavoro 656c23g
![]()
Abbiamo indicato con i0 l'entalpia finale, con Ec0 l'energia cinetica finale (che è nulla), con i e con Ec l'entalpia e l'energia cinetica iniziale:
![]() (1)
(1)
Otteniamo in questo modo l'espressione dell'entalpia totale del fluido, cioè il valore di entalpia posseduto dal fluido al termine della decelerazione.
In una trasformazione adiabatica in cui non c'è scambio di lavoro 656c23g abbiamo che:
![]() (2)
(2)
cioè l'entalpia totale si conserva.
Se il fluido è un gas perfetto abbiamo che:
![]() (3)
(3)
Nelle stesse condizioni della (2) anche la temperatura totale si conserva:
![]() (4)
(4)
Durante la decelerazione del fluido l'entropia rimane costante, perché abbiamo detto che la decelerazione deve essere isoentropica. Quindi, indicando con S1 l'entropia prima della decelerazione e con S10 l'entropia dopo la decelerazione , abbiamo:
![]()
In una trasformazione generica in cui c'è un variazione di entropia S2 - S1 , si ha che:
![]() (5)
(5)
Inoltre, se il fluido è un gas perfetto abbiamo che:
![]()
e se la trasformazione è adiabatica e senza scambio di lavoro 656c23g , cioè è vera la (4), abbiamo che:
![]()
Da questa relazione si deduce che, in una trasformazione adiabatica, senza scambio di lavoro 656c23g e isoentropica (S2=S1), la pressione totale si conserva:
![]()
Partiamo dall'equazione di continuità:
![]() (6)
(6)
la portata in massa è costante perché stiamo trattando una corrente stazionaria; calcoliamo il logaritmo di questa espressione e poi deriviamo (derivata logaritmica):
![]() (7)
(7)
Dall'equazione di conservazione dell'energia:
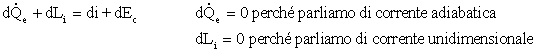
quindi otteniamo:
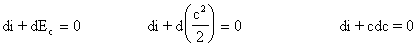 (8)
(8)
Se scriviamo l'equazione di conservazione dell'energia in quest'altra forma:
![]()
![]()
![]()
introducendo questa espressione nella (8):
![]()
Ora, ricordando la definizione di velocità del suono:
![]() (9)
(9)
Introduciamo questo termine nell'equazione di continuità:
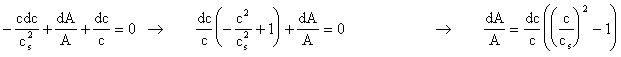
introduciamo il numero di Mach:
![]()
(quando Ma>1 la velocità c è maggiore del suono ).
Quindi otteniamo:
![]() (10)
(10)
Possiamo scrivere la (10) in una forma diversa in cui compaia la pressione:
![]()
Riprendendo la (9), possiamo scrivere:
![]()
sostituendo nella (10):
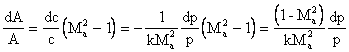 (11)
(11)
Queste espressioni valgono sia per un condotto accelerante, effusore o ugello, nel quale un fluido comprimibile subisce un'espansione con un aumento della velocità, sia per un condotto decelerante, diffusore, nel quale il fluido subisce una diminuzione di velocità e corrispondentemente un aumento di pressione.
Consideriamo il percorso di un fluido attraverso un ugello, dall'ambiente 1 all'ambiente 2:


All'ingresso dell'ugello il fluido si trova ad una pressione p1, ad una temperatura T1 e possiede una velocità c1; all'uscita dell'ugello abbiamo una pressione p2 minore di p1, una temperatura T2 e una velocità c2 maggiore di c1.
Tenendo conto delle equazioni (10) e (11), facciamo le seguenti considerazioni.
Se la velocità c del fluido è subsonica, cioè c<cs, si ha Ma<1; noi
vogliamo ottenere una accelerazione del fluido, cioè vogliamo che sia ![]() ; dalla (10) segue che dobbiamo avere
; dalla (10) segue che dobbiamo avere ![]() , ma allora dalla (11) deduciamo che
, ma allora dalla (11) deduciamo che ![]() . In conclusione, per ottenere un'accelerazione occorre avere
un condotto convergente e otteniamo
una diminuzione di pressione.
. In conclusione, per ottenere un'accelerazione occorre avere
un condotto convergente e otteniamo
una diminuzione di pressione.
Se la velocità c del fluido è supersonica, cioè c>cs, si ha Ma>1; noi
vogliamo ottenere una accelerazione del fluido, cioè vogliamo che sia ![]() ; dalla (10) segue che dobbiamo avere
; dalla (10) segue che dobbiamo avere ![]() , ma allora dalla (11) deduciamo che
, ma allora dalla (11) deduciamo che ![]() . In conclusione, per ottenere un'accelerazione occorre avere
un condotto divergente e otteniamo
una diminuzione di pressione.
. In conclusione, per ottenere un'accelerazione occorre avere
un condotto divergente e otteniamo
una diminuzione di pressione.
Se la velocità c del fluido è molto vicina quella del
suono (corrente transonica), cioè c=cs,
si ha Ma=1; dalla (10) segue che dobbiamo avere ![]() , e dalla (11) deduciamo che
, e dalla (11) deduciamo che ![]() . In conclusione il fluido si muove con sezione costante e
non c'è variazione di pressione.
. In conclusione il fluido si muove con sezione costante e
non c'è variazione di pressione.
In generale, a seconda dei valori iniziali e finali di pressione e velocità, utilizzeremo un condotto solo convergente, o solo divergente, o convergente e divergente, ecc.
Consideriamo il percorso di un fluido attraverso un diffusore, dall'ambiente 1 all'ambiente 2:



All'ingresso del diffusore il fluido si trova ad una pressione p1, ad una temperatura T1 e possiede una velocità c1; all'uscita del diffusore abbiamo una pressione p2 maggiore di p1, una temperatura T2 e una velocità c2 minore di c1.
Tenendo conto delle equazioni (10) e (11), facciamo le seguenti considerazioni.
Se la velocità c del fluido è subsonica, cioè c<cs, si ha Ma<1; noi
vogliamo ottenere una decelerazione del fluido, cioè vogliamo che sia ![]() ; dalla (10) segue che dobbiamo avere
; dalla (10) segue che dobbiamo avere ![]() , ma allora dalla (11) deduciamo che
, ma allora dalla (11) deduciamo che ![]() . In conclusione, per ottenere una decelerazione occorre
avere un condotto divergente e
otteniamo un aumento di pressione.
. In conclusione, per ottenere una decelerazione occorre
avere un condotto divergente e
otteniamo un aumento di pressione.
Se la velocità c del fluido è supersonica, cioè c>cs, si ha Ma>1; noi
vogliamo ottenere una decelerazione del fluido, cioè vogliamo che sia ![]() ; dalla (10) segue che dobbiamo avere
; dalla (10) segue che dobbiamo avere ![]() , ma allora dalla (11) deduciamo che
, ma allora dalla (11) deduciamo che ![]() . In conclusione, per ottenere un decelerazione occorre avere
un condotto convergente e otteniamo
un aumento di pressione.
. In conclusione, per ottenere un decelerazione occorre avere
un condotto convergente e otteniamo
un aumento di pressione.
Se la velocità c del fluido è molto vicina quella del
suono (corrente transonica), cioè c=cs,
si ha Ma=1; dalla (10) segue che dobbiamo avere ![]() , e dalla (11) deduciamo che
, e dalla (11) deduciamo che ![]() . In conclusione il fluido si muove con sezione costante e
non c'è variazione di pressione.
. In conclusione il fluido si muove con sezione costante e
non c'è variazione di pressione.
Studiamo un fluido che in una sezione generica del condotto possiede una velocità c e una pressione p. Come ipotesi iniziale poniamo che la velocità iniziale del fluido (all'ingresso del condotto) sia zero. Partiamo dalla legge di conservazione dell'energia, ricordando che parliamo di flussi adiabatici e isoentropici:
![]()
infatti, come abbiamo detto, c1=0. Otteniamo quindi:
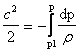 (12)
(12)
Dall'equazione dei gas perfetti per una trasformazione isoentropica sappiamo che:
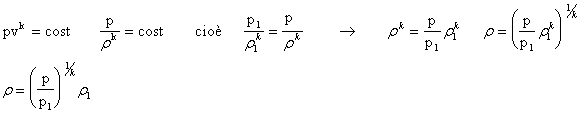
Sostituendo quest'ultima espressione nella (12):
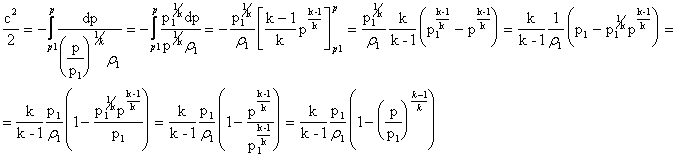
Da questa relazione ricaviamo la velocità del fluido:
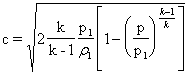
Dall'equazione di continuità sappiamo che la sezione del condotto è inversamente proporzionale a rc:
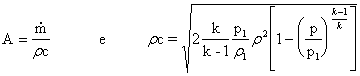
ricordando che:
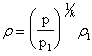
otteniamo che la sezione A è inversamente proporzionale alla quantità:
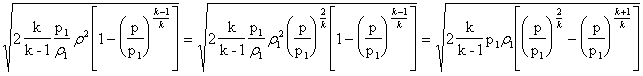
Il massimo di rc, che corrisponde al minimo di A, si ottiene derivando quest'ultima
espressione rispetto a ![]() ; il risultato che si
determina è il seguente:
; il risultato che si
determina è il seguente:
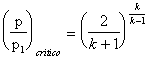
![]() Questo significa che, quando il rapporto tra la pressione del
fluido e la sua pressione iniziale è pari al rapporto critico, la sezione del
condotto è minima e la velocità è massima. Nota che il rapporto critico dipende
solo da k e nei casi reali ha un
valore intorno a 0,5.
Questo significa che, quando il rapporto tra la pressione del
fluido e la sua pressione iniziale è pari al rapporto critico, la sezione del
condotto è minima e la velocità è massima. Nota che il rapporto critico dipende
solo da k e nei casi reali ha un
valore intorno a 0,5.
Se, come abbiamo supposto all'inizio, la velocità iniziale c1 non è pari a zero, otteniamo la stessa espressione, in cui però al posto della pressione p1 c'è la pressione totale p10 e al posto del volume massico c'è il volume massico totale:
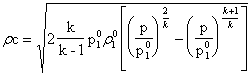 (13)
(13)
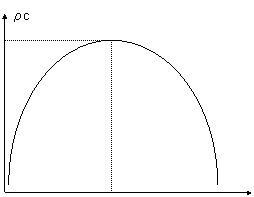
Se rappresentiamo la velocità c in funzione del rapporto p/p1
otteniamo la curva a sinistra. In prossimità del rapporto critico si ha la
massima velocità. Analogo grafico si ottiene sostituendo le grandezze in
gioco con le rispettive grandezze totali. p/p1 p/p1 critico
Consideriamo un ugello semplicemente convergente:
ambiente 2

Quando la pressione all'uscita del condotto, pu, è uguale alla pressione dell'ambiente 2, parliamo di ugello adattato; se ci poniamo in questa condizione, possiamo riscrivere l'equazione di continuità in questo modo:
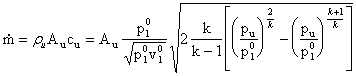 (14)
(14)
ru è la densità del fluido alla sezione di uscita, Au è la sezione di uscita, cu è la velocità del fluido alla sezione di uscita. Infatti, riprendendo la (13), e ponendo p=pu:
![]()
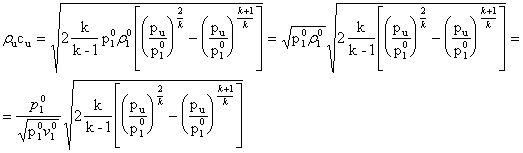
L'espressione (14) ci fornisce la portata in massa alla sezione di uscita nel caso di ugello adattato.
Ora vogliamo vedere cosa succede quando facciamo variare la pressione nell'ambiente 2, p2, mantenendo costanti p10 e r
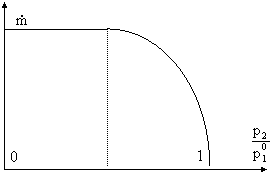
Se tracciamo il diagramma relativo alla (14), otteniamo una curva di questo tipo:
Studiamo il valore di p2
nell'intervallo [0-p10]; ai due estremi di tale
intervallo la portata è nulla, come si deduce dalla (14).
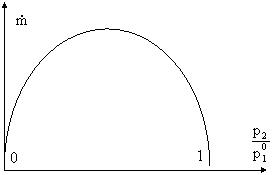
In realtà il fluido non si comporta nel modo descritto dal grafico.
Partendo da p2= p10, e diminuendo p2 verso 0, la velocità (quindi la portata) del fluido aumenta fino a raggiungere il valore massimo. In questo tratto l'ugello è adattato, cioè abbiamo che p2=pu. Il massimo è raggiunto quando p2/p10 è pari al rapporto critico, cioè quando:
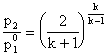
In corrispondenza di questa pressione, nella sezione di uscita si realizza la velocità critica, pari alla velocità del suono; in questo punto la portata in massa è pari a:
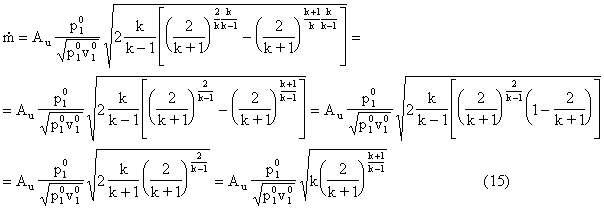
Diminuendo ancora p2, la perturbazione che si crea in conseguenza di questa diminuzione, si muove verso l'ambiente 1 con la velocità del suono, ma il fluido si muove verso l'ambiente 2 con la stessa velocità, quindi l'ambiente 1 non avverte le modifiche che avvengono nel 2 e la velocità del fluido non cambia; nel tratto a sinistra del massimo l'ugello non è più adattato, cioè la pressione alla sezione di uscita rimane costante, mentre la pressione dell'ambiente 2 diminuisce:
A sinistra del rapporto critico la portata
in massa mantiene il valore massimo dato dalla (15).
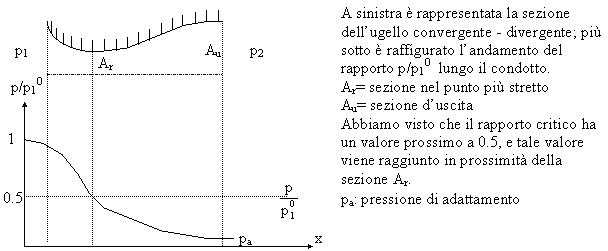
Proviamo a diminuire la pressione p2, a partire dal valore p2 = p10 , mantenendo costanti le condizioni a monte dell'ugello:
a: p2 = p10 , la pressione è uguale
a p10 in tutto il condotto; non c'è movimento perché
non c'è differenza di pressione tra monte e valle; b,c: p2 < p10 , il flusso è
ovunque subsonico: accelera nella prima sezione e decelera nella seconda;
la pressione all'uscita è pari a p2 (adattato);
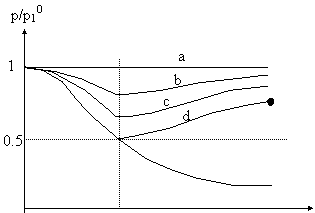
d: il valore p/p10
raggiunto all'uscita è detto discriminante:
se 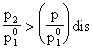 , l'ugello è subsonico, se
, l'ugello è subsonico, se 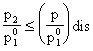 in almeno un punto
dell'ugello il flusso raggiunge la velocità del suono. Nel caso della curva d il flusso raggiunge la pressione
critica e la velocità del suono solo nel punto più stretto, dopodiché si ha una
diffusione e il flusso ritorna subsonico.
in almeno un punto
dell'ugello il flusso raggiunge la velocità del suono. Nel caso della curva d il flusso raggiunge la pressione
critica e la velocità del suono solo nel punto più stretto, dopodiché si ha una
diffusione e il flusso ritorna subsonico.
Se continuiamo a diminuire p2, il flusso nella prima sezione sarà, per un tratto, supersonico, poi avverrà un salto di pressione (urto retto o obliquo) nella seconda sezione o, al limite, sulla sezione di uscita:
Nella figura è mostrato cosa succede
quando avviene un urto: : tratto supersonico : urto : tratto subsonico Se p2 è minore della pressione
di adattamento, l'espansione non avviene più nel condotto ma al di fuori di
esso, oltre la sezione d'uscita.
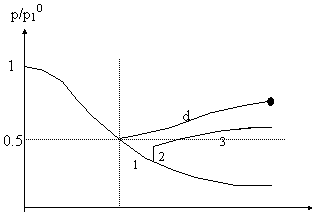
Riassumendo, l'ugello convergente - divergente diventa critico quando:
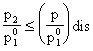
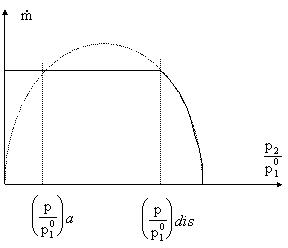
Vediamo ora l'andamento della portata:
Come si vede dal grafico, fino a che la
pressione p2 rimane superiore alla pressione discriminante, la
portata del flusso aumenta secondo l'equazione (14) (semiellisse). In
questa situazione la pressione all'uscita è pari alla pressione p2;
quando p2 raggiunge la pressione discriminante, e da quel punto
in poi, la portata rimane costante, con un valore dato dalla (15) (retta
orizzontale).
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026