Teoria delle Catastrofi

La nazione di "organizzazione" evidenzia un processo che si dimostra innanzi tutto imprevedibile, non deterministico, partecipe al tempo stesso di ORDINE e DISORDINE, di condizioni di equilibrio e di non equilibrio. Alla luce di questo la natura ci si presenta sempre più come una realtà difficilmente determinabile. Essa si presenta imprevedibile e disponibile verso sempre nuove ed inedite possibilità di sintesi le quali prendono inevitabilmente corpo qualora si verifichino certe circostanze. La nuova visione della natura dunque oscil 919d32j la tra condizioni vincolanti e libertà tra loro dinamicamente convesse. Evidentemente questo conferisce un certo valore all'idea che nella natura vi sia un certo progresso, una sua storia, che non è tuttavia assolutamente indicabile. Come ha giustamente osservato Italo Mancini a proposito della teoria delle catastrofi elaborata da René Thomson, sono ora di fronte ad una ribellione in favore del nuovo, dell'inedito, del dispotismo. Le ragioni del diverso di fronte all'identico. La natura al contrario di quanto sostiene Manod, non si trova in un equilibrio morto, dove l'organizzazione del vivente è semplicemente un'eccezione e dove non ci sono le idee di progresso e libertà, ma bensì è qualcosa di organizzato da leggi che regolano il processo tra ordine e disordine. Di conseguenza possiamo affermare che l'universo è in continua trasformazione è in progresso per le sue intrinseche possibilità e trova spiegazione non dentro di sé, ma altrove. Questo suggerimento è alla base dell'attuale riflessione sulla natura. Tale apertura conferisce maggior spazio alla libertà umana che resta irriducibile rispetto ad ogni tentativo di dominio o di comprensione della natura. Ciò restituisce un valore positivo all'uomo che, senza sentirsi schiacciato dalla natura, vi si avvicina per trascenderla.

Di questa apertura partecipa anche il sapere scientifico stesso. Infatti la natura ci si mostra sempre come circoscritta entro i molteplici linguaggi della scienza; di qui l'impossibilità inoltre di sbarazzarci delle nostre conoscenze che sono sempre linguisticamente confinate entro "mappe" o "modelli" che ovviamente non sono la realtà, bensì livelli o aspetti particolari di essa, che resta in sé attingibile.

E in questo spazio di irriducibilità teorica e pratica che si situa una diversa intelligibilità della natura; un'intelligibilità che è estremamente dipendente dai condizionamenti del nostro conoscere .

Cimentarsi nella ricerca di una definizione esauriente dei fermenti del nostro tempo appare un'impresa quanto mai rischiosa e, sotto parecchi aspetti, sterile. Il compito sarebbe più facile e interessante se ci si limitasse ad un'analisi condotta attraverso l'individuazione di alcune parole chiave, intese come guide per posare lo sguardo sulla realtà. Una di queste parole da usare come lente di ingrandimento, soprattutto per esplorare il campo del sapere a noi più vicino, quello della filosofia e della scienza, potrebbe essere senz'altro il termine "crisi". La storia del pensiero scientifico e filosofico contemporaneo è infatti segnata, già a partire dalla fine del XIX secolo dalla progressiva presa di coscienza di un lento ma inesorabile dileguarsi delle certezze, dei fondamenti teorici e pratici del sapere. Uno alla volta, tutte le categorie del pensare e dell'agire scientifico e filosofico, idee e concetti ritenuti immutabili come il tempo, lo spazio, il rapporto tra cause ed effetto, sono stati messi alla prova.

Assunta consapevolezza di ciò, su un piano più teorico ed intellettuale si è ritenuto che una delle possibili linee di azione fosse, da un lato, quella di trovare nuove risposte, più adeguate al tempo che stiamo vivendo, agli interrogativi classici della filosofia, intesa ancora come sguardo critico sul mondo; dall'altro, si è cercato di costruire un'immagine il più possibile confortante del lavoro e delle prospettive della scienza, la quale ha mantenuto la speranza di continuare a ricoprire il ruolo ereditato dal tempo di Newton e Galileo. Su un piano meno astratto, la crisi che caratterizza il nostro secolo è però una crisi di tipo esistenziale, profonda e diffusa a livello globale; nessun aspetto della nostra vita ne è immune, a partire da questioni come la salute, i mezzi di sussistenza, la qualità dell'ambiente e dei rapporti sociali, l'economia, la tecnologia. Si è sviluppata insomma la coscienza di una serie impressionante di emergenze, che coinvolgono l'umanità, a tutti i livelli in un tentativo di ricerca di nuove soluzioni. L'immagine stessa della filosofia e della scienza ne risulta quindi modificata: il sapere ereditato dall'età moderna, per poter sopravvivere, deve mettere in discussione uno dopo l'altro tutti i suoi fondamenti, ma soprattutto deve scoprirsi ancora capace di calarsi nella vita reale, e rispondere alle domande sempre più pressanti che essa gli pone.

Tratto dall'intervista "Teoria delle catastrofi" - Parigi, Istituto di Matematica, studio, venerdì 16 dicembre 1988

La teoria delle catastrofi ha un programma che è facile da esporre: si tratta di spiegare le forme naturali. Quando posiamo il nostro sguardo sul mondo, costatiamo che l'universo non è un caos, che è diviso in forme relativamente distinte, ben separate le une dalle altre. E' più simile all'ordine di un cosmo che non un caos. Da questo punto di vista, ciò che la teoria delle catastrofi tenta di fare è di esplicare l'origine e la successione delle forme naturali così come le percepiamo nel mondo che ci circonda.

Questo punto di vista della teoria delle catastrofi è abbastanza nuovo, nel senso che essa si propone di edificare una teoria che spieghi la genesi delle forme indipendentemente dal substrato materiale che le compone. Questo ha qualcosa di un po' paradossale, perché sappiamo per certo che una nuvola non ha la stessa consistenza di un blocco di marmo, e che di conseguenza la permanenza delle forme è strettamente legata alla natura del loro substrato. Non ci sono dubbi sul fatto che la natura del substrato abbia effettivamente un ruolo di primo piano nel determinare il carattere più o meno permanente, o al contrario più o meno transitorio, di una forma. Ma, ciononostante, la teoria delle catastrofi adotta un punto di vista risolutamente indipendente dal substrato. In altre parole, ci si pone in un'ottica per cui c'è qualcosa come un etere soggiacente che riempie tutto lo spazio. Una materia prima, avrebbe detto Aristotele. Questa materia prima è sottomessa a delle sollecitazioni che le fanno adottare questo o quell'altro tipo di materia. Quello che la teoria delle catastrofi propone sono gli schemi generali che permettono di spiegare la genesi delle forme. Facciamo l'esempio del piano della scrivania, che è qui davanti a me: abbiamo uno spigolo che separa la superficie orizzontale della scrivania dalla parete verticale. Questo spigolo per me è un luogo di catastrofe, perché separa due superfici che hanno delle funzioni e degli orientamenti diversi. La natura del substrato è evidentemente la stessa: dell'aria da una parte e del legno dall'altra. Ma se si vuole risalire all'origine delle forme, ci si renderà conto che questo spigolo trae origine dal fatto che l'asse di legno che costituisce la scrivania è stata inizialmente segata da una sega, diciamo metallica, il cui disco ha tracciato una linea di contorno nel legno dell'asse. Ed è il conflitto fra l'acciaio della sega e la materia legno che ha generato la forma. La teoria delle catastrofi ritorna alla vecchia idea eraclitea che il conflitto è il padre di tutte le cose. Qualsiasi forma deve la sua origine ad un conflitto.

Teoria Matematica

La teoria delle catastrofi ( la TC ) è un metodo matematico generale. Essa vuole proporre un modello descrittivo per rendere conto qualitativamente di fenomeni discontinui. Intende classificare queste discontinuità (o catastrofi) in base alle loro caratteristiche topologiche. Questa teoria è stata ideata da René Thom (nato nel 1923), professore di matematica all'Institut des Hautes Etudes Scientifiques à Bures-sur-Yvette (Francia). Già negli anni Sessanta Thom si occupava dell'elaborazione della TC, ma il vero successo egli lo ottenne nel 1972 con la pubblicazione di Stabilité Structurelle et Morphogénèse.

Nella prefazione al libro in questione troviamo questa affermazione di C.H. Waddington, professore di genetica animale all'università di Edimburgo:

"I am honoured to have been invited to write a preface to Dr. René Thom's Stabilité Structurelle et Morphogénèse. I cannot claim to understand all of it; I think that only a relatively few expert topologists will be able to follow all his mathematical details; and they may find themselves less at home in some of the biology."

Il problema fondamentale è dunque: come un non-matematico potrebbe capire il ragionamento sofisticatissimo di Thom? La risposta è semplice: non può e non deve. Ritorniamo alla nostra definizione e cominciamo con l'ultima parte. Ogni catastrofe ha delle caratteristiche topologiche proprie che permettono di definirla nei termini di sette catastrofi elementari. La descrizione di una discontinuità richiede una matematizzazione di due specie di dimensioni: le dimensioni di controllo e le dimensioni di comportamento. Così si può enunciare il teorema secondo cui esistono soltanto sette tipi di catastrofi elementari per quattro variabili di controllo (o meno) e qualsiasi quantità di variabili di comportamento. Queste sono le sette catastrofi elementari:

I. LE CUSPIDI (una dimensione di comportamento)

1. la piega: una dimensione di controllo

2. la cuspide: due dimensioni di controllo

3. la coda di rondine: tre dimensioni di controllo

4. la farfalla: quattro dimensioni di controllo

II. GLI OMBELICHI (due dimensioni di comportamento)

5. l 'iperbolico: tre dimensioni di controllo

6. l 'elittico: tre dimensioni di controllo

7. il parabolico: quattro dimensioni di controllo

Ogni catastrofe elementare ha un suo centro organizzatore e un dispiegamento universale caratteristico. Questi due concetti matematici permettono di raggruppare i processi naturali in insiemi più vasti che costituiscono un "linguaggio". Questo ragionamento si riassume nelle sei tesi di Thom di cui diamo qui l'elenco:

Tout objet, ou toute forme physique, peut être représentée par un attracteur C d'un système dynamique dans un espace M de variables internes.

Un tel objet ne présente de stabilité, et de ce fait ne peut être aperçu, que si l'attracteur correspondant est structurellement stable.

Toute création ou destruction de formes, toute morphogénèse, peut être décrite par la disparition des attracteurs représentant les formes initiales et leur remplacement par capture par les attracteurs représentant les formes finales. Ce processus, appelé catastrophe, peut être décrit sur un espace P de variables externes.

Tout processus morphologique structurellement stable est décrit par une (ou un système de) catastrophe(s) structurellement stable(s) sur P.

Tout processus naturel se décompose en îlots structurellement stables, les chréodes. L'ensemble des chréodes et la syntaxe multidimensionnelle qui régit leurs positions respectives constitue un modèle sémantique.

Si l'on considère une chréode C comme un mot de ce langage multidimensionnel; la signification de ce mot n'est autre que la topologie globale du (ou des) attracteur(s) associé(s) et celle des catastrophes qui la subissent. En particulier, pour un attracteur donné, la signification est définie par la géométrie de son domaine d'existence sur P et la topologie des catastrophes de régulation qui limitent ce domaine.

Teoria Generale

Anche se la TC è nata in un campo strettamente matematico, la sua importanza risiede nel progetto di geometrizzare quelle scienze che hanno resistito a lungo ad un'analisi matematica: la biologia e le scienze umane, vale a dire le scienze inesatte. In questo modo, la TC si differenzia dalle cosiddette teorie scientifiche perché essa non richiede necessariamente una conferma sperimentale.

Innanzitutto bisogna aver chiaro che la teoria delle catastrofi non è una teoria scientifica nel senso usuale del termine. Non è cioè una teoria scientifica come lo sono, per esempio, la teoria della gravitazione di Newton, la teoria dell'elettromagnetismo di Maxwell o anche la teoria dell'evoluzione di Darwin. Teorie del genere devono essere confermate dall'esperienza, che si possano cioè addurre argomenti sperimentali a loro favore.
Ma la teoria delle catastrofi non deve affatto soddisfare questa richiesta. Il termine "teoria" va inteso in un senso molto particolare: direi piuttosto che si tratta di una metodologia, se non di una sorta di linguaggio, che permette di organizzare i dati dell'esperienza nelle condizioni più varie.

Da questo brano, tratto da un'intervista con René Thom, escono due punti importanti, costanti negli scritti dei seguaci della TC: il rifiuto di accettare il controllo sperimentale tra i criteri che danno diritto di esistenza ad una teoria scientifica, e la ricerca di una metodologia capace prima di tutto di classificare fenomeni di diversa natura. L'esigenza empirica (il controllo sperimentale) lega necessariamente la generalità della teoria alla contingenza dei dati dell'esperienza. La negazione di tale esigenza può indurre la TC a generalizzare la portata delle applicazioni (teoriche, s'intende), senza che questa estensione debba incidere sulla teoria stessa.

Ma qual'è la relazione tra la matematica e le scienze umane secondo Thom, ossia perché occuparsi di scienze inesatte?

La matematica è difficile, ma penso che anche la fisica teorica presenti delle autentiche difficoltà. Mentre non ci sono analoghe difficoltà intellettuali in altri campi di ricerca. Secondo me, c'è una differenza qualitativa fra la matematica e la fisica teorica da un lato e le altre discipline dall'altro. Queste ultime, credo sono a un livello intellettuale inferiore.

Quindi per Thom, solo il matematico ha il diritto di essere "intelligente". La ragione di questa supremazia non è molto chiara, ma ci pare che essa vada cercata appunto nella purezza teorica della matematica, disciplina autonoma priva del peso sperimentale. Si tratta quindi di elaborare una teoria matematica a priori per applicarla poi al mondo empirico. Inoltre, la TC permette di trascurare i concetti delle scienze umane per collegare i diversi oggetti di queste scienze in un linguaggio unico:

Si l'on veut poursuivre à l'égard de ces concepts [delle scienze umane] une forme, même réduite, du programme hilbertien d'élimination du sens, alors l'étape de géométrisation par la TC peut apparaître comme un intermédiaire très précieux: on remplace alors l'intuition sémantique, avec son caractère subjectif immédiat, par l'intuition géométrique, qui spatialise son objet, et le distancie du sujet pensant.

La TC , en ce qu'elle est fondamentalement une théorie locale, élimine le caractère non local, trans-spatial, quasi magique de ces notions.

Da ciò che precede risulta chiaro che la TC si considera come una teoria oggettiva, generale e quindi interdisciplinare. È quindi evidente che i discorsi della TC sono contrassegnati da un ottimismo scientifico ad oltranza. Ecco ne un bel esempio:

L'on entrevoit désormais la possibilité de prolonger le rationalisme physique en un rationalisme structural, mathématiquement fondé, intégrant en la légalisant sa ``part maudite'' phénoménologique, symbolique et sémiotique; la possibilité, dans le cadre d'une extension objective de l'ontologie naturelle, de naturaliser un ordre rationnel du sens qui, jusqu'ici oscillait entre sa réification formaliste et son monnayage existentiel; bref, la possibilité d'une nouvelle philosophie naturelle rectifiant critiquement le partage (le ``Yalta'' transcendantal) entre Naturwissenschaften et Geisteswissenschaften, et venant faire du labyrinthe que Michel Serres a si joliment appelé ``le passage du Nord-Ouest'' le chemin et la voie vers, osons dire le mot, une nouvelle Aufklärung.

Caotica

Non esistono due cristalli di neve uguali (*)

La Caotica è la scienza che studia il "Caos", cioè l'apparente mancanza di regole o di Leggi naturali. E' nata negli anni '70 per tentare di prevedere il tempo meteorologico ma, soprattutto, nel tentativo di giungere a una Teoria dei "campi unificati", e cioè a una Legge o insieme di Leggi che unifichino i campi elettrico, magnetico, gravitazionale, ecc.,  a cui si era già dedicato Einstein negli ultimi anni della sua vita. E' noto "l'effetto farfalla": una farfalla sbatte le ali a Roma e tre giorni dopo su Pechino si abbatte una tempesta. Questo per spiegare che le variabili che fanno cambiare il tempo sono così tante e così piccole che non si può prevederle e prevederne gli effetti cumulativi. La Caotica è la ricerca di una regola dove in apparenza non ce ne sono. Necessita quindi di un approccio sperimentale, cioè per tentativi e verifiche a posteriori, con l'obiettivo di trarre regole di tipo generale, applicabili a più occasioni. Se ne occupano attualmente i migliori scienziati del mondo, in Università come il Caltech, il MIT, il Santa Fe Institute.

(*) La Caotica si occupa di tutti i fenomeni che, almeno in apparenza, non sono riconducibili a un'unica Legge, e cerca se tale legge esista e quale sia: se ci sia, cioè e comunque, un Ordine anche dove non sembrerebbe esserci (Caos). Un altro esempio tipico sono i cristalli dei fiocchi di neve: perché non ne esistono due uguali? La Caotica studia anche questo fenomeno.

Le Leggi del Caos

Gli studi sul Caos hanno però già portato a delle "scoperte" che hanno permesso di enunciare due Leggi generali:

Prima Legge del Caos
Qualsiasi sistema in equilibrio instabile, è destinato a subire un'esplosione "caotica" che lo trasformerà in un sistema più piccolo ma più stabile.

Seconda Legge del Caos
Tutti gli avvenimenti "maggiori" apparentemente inattesi non sono altro che la somma di tanti avvenimenti "minori" passati inosservati.

La Caotica nella vita quotidiana
Un gatto ha starnutito...

Anche la nostra vita di tutti i giorni è dominata dalla Caotica: noi viviamo di rapporti sociali e di interazione con gli altri. E' impossibile prevedere tutte le implicazioni, nel tempo e nello spazio, di una nostra azione, perché essa spingerà altre persone a reagire e noi non sappiamo come. Spesso un nostro atto determina una serie di avvenimenti non controllabili e non prevedibili. Proprio come nel caso "dell'effetto farfalla" nel tempo meteorologico, esiste nei rapporti sociali una cosa chiamata "effetto starnuto", per cui un gatto starnutisce a Milano e, sempre magari a Pechino, scoppia una rivoluzione (è una storiella molto divertente scritta 30 anni fa circa da un noto scienziato-divulgatore). Non è un paradosso o una esagerazione; può capitare. Pensate solo a quante volte una semplice parola da voi pronunciata ha avuto, dopo molti giri e passaggi, degli effetti, magari seri, che non avevate minimamente previsto.

in principio era il caos
La possibilità che si possa prevedere con esattezza l'evoluzione nel tempo di un sistema in cui sono note tutte le forze agenti e le posizioni reciproche degli oggetti che lo compongono è ciò che gli scienziati chiamano determinismo. Da circa un secolo essi sanno che questa possibilità è irrealizzabile per la maggior parte dei sistemi a più oggetti in evoluzione. Esiste tutta una serie di fenomeni, detti caotici, per i quali previsioni di comportamento a lungo termine non sono possibili.
Per conoscere l'evoluzione di un sistema bisogna conoscerne le condizioni iniziali. Ma nessuna misura può avere una precisione assoluta: essa contiene sempre in sé un'incertezza. Sfortunatamente questa incertezza non rimane costante al passare del tempo e anzi non fa che aumentare.
I sistemi caotici presentano una grande "sensibilità alle condizioni iniziali": due situazioni di partenza molto simili (o che addirittura la precisione della nostra misura ci permette di considerare uguali) con il passare del tempo possono evolversi in modo molto differenziato. Da ciò consegue una forte irregolarità di comportamento. Tutto ciò che è veramente regolare è abbastanza prevedibile. Ma una grande sensibilità alle condizioni iniziali rende un sistema imprevedibile - dunque irregolare. Questo è quello che colloquialmente viene detto "effetto farfalla": quando una farfalla batte le ali a Tokio, può scatenarsi un uragano in Florida un mese più tardi, o, detto altrimenti, un dettaglio che inizialmente appare trascurabile, alla lunga può avere effetti importanti.
Il caos non è solamente un comportamento complicato e senza motivo apparente, il concetto è ben più sottile. Il caos ha le apparenze della complicazione ma la spiegazione è semplice: esso segue leggi deterministiche anche se appare disordinato e imprevedibile.

Attrattori strani
Lo studio dei fenomeni caotici è stato reso possibile dall'introduzione, poco più di un secolo fa, di una geometrizzazione della meccanica ad opera del matematico francese Henri Poincaré. Egli inventò il concetto di "spazio delle fasi", uno spazio matematico immaginario che rappresenta tutti i movimenti possibili di un sistema dinamico dato. Si può rappresentare lo stato di un sistema con un punto in un piano in un sistema di coordinate (non necessariamente spaziali, si tratta delle grandezze da cui dipende l'evoluzione del sistema). Se facciamo scorrere il tempo, le coordinate assumono valori diversi e il punto nel piano si sposta. Un punto che si sposta descrive una curva e questa curva è una rappresentazione del futuro dell'intero sistema. In realtà basta guardare la curva per vedere le caratteristiche dell'evoluzione di questo sistema, senza dover per forza considerare in dettaglio i valori numerici delle coordinate. Se per esempio la curva tende ad un certo punto e poi si ferma lì, ciò significa che il sistema raggiunge un punto di equilibrio da cui non si sposta più. Se la curva si chiude, vuol dire che il sistema si evolve con un ritmo periodico, assumendo a intervalli definiti gli stessi valori. Se scegliamo valori iniziali diversi, otteniamo una nuova curva: in questo modo possiamo vedere tutti i comportamenti possibili del sistema.

Uno dei frutti dell'innovazione di Poincaré è che nello spazio delle fasi appaiono delle forme geometriche, dette attrattori, che permettono di visualizzare la dinamica del sistema. Facendo partire un sistema dinamico da un punto dato e considerando la sua evoluzione a lungo termine, si constata frequentemente che esso finisce per essere confinato in una certa regione dello spazio delle fasi. Per esempio un sistema che evolve verso un punto di equilibrio è un sistema con un attrattore e questo attrattore è il punto stesso. Un sistema che finisce per ripetere indefinitamente lo stesso ciclo, come può essere un pendolo che si muove senza attrito, ha un attrattore che è un anello. La dinamica dei sistemi a lungo termine è regolata dagli attrattori e la loro forma determina il tipo di dinamica che si produrrà.

La geometria del caos è piuttosto particolare: ad essa sono associati degli attrattori definiti strani, nell'intorno dei quali il movimento dettagliato non può essere determinato in anticipo. Questo è conseguenza dell'effetto farfalla. Pensate ad una pallina da ping-pong lanciata in un mare oleoso. Che la facciate cadere dall'alto o la lasciate andare sotto la superficie, essa si dirigerà verso la superficie. Una volta lì, seguirà una traiettoria complessa in mezzo alle onde, ma rimarrà in superficie, o per lo
meno molto vicino ad essa, per quanto complessa sia questa traiettoria. La superficie del mare può essere una buona immagine di un attrattore strano.

Sui sistemi caotici si possono fare molte previsioni: per esempio si può distinguere un sistema caotico da un sistema realmente casuale. Spesso si può prevedere la forma di un attrattore, forma che non è modificata dall'effetto farfalla.

Determinismo e caos
La scoperta del caos ha rivelato la confusione fondamentale che esiste in noi fra le leggi e i comportamenti che queste leggi generano - confusione fra le cause e i loro effetti. Pensavamo che cause deterministe dovessero avere effetti regolari, ma ora vediamo che possono avere effetti molto irregolari, che possono essere confusi con effetti aleatori. Pensavamo che cause semplici producessero effetti semplici (e implicitamente che cause complesse avessero effetti complessi) ma ora sappiamo che cause semplici possono avere effetti complessi. Comprendiamo che conoscere le leggi e essere capaci di prevedere il futuro sono due cose diverse.

Questi risultati hanno trovato applicazioni in molteplici studi, i più noti dei quali riguardano la meteorologia e le previsioni del tempo, ma si sono verificate interessanti applicazioni del caos al battito cardiaco, alle onde elettroencefalografiche, alla dinamica delle popolazioni, al campo magnetico terrestre, alla traiettoria degli asteroidi del nostro sistema solare e dei satelliti artificiali, alle turbolenze intorno ad un sottomarino o un aereo, alla borsa e ai titoli finanziari.solo per fare alcuni esempi.

Mettere ordine nel caos
Negli ultimi decenni gli scienziati stanno studiando come "metter ordine" nel caos. I risultati indicano che il caos è quantificabile in modo preciso, esprimibile addirittura mediante un numero intero. Esiste pertanto una ben determinata gerarchia nel comportamento caotico: più è grande questo intero, più il caos del sistema è marcato. In secondo luogo hanno dimostrato anche sperimentalmente che il passaggio dall'ordine al caos avviene gradualmente per di più seguendo uno scenario invariabile, le cui singole tappe sono qualitativamente le stesse per i sistemi dinamici più disparati. L'analisi dettagliata di tale passaggio è il risultato di una felice sinergia di azione fra una profonda teoria matematica (la teoria KAM) ed i moderni metodi numerici e computazionali.
Oggi si ritiene che il caos, ancorché innescato da un'azione esterna (come la variazione delle condizioni iniziali), nasca in realtà dal sistema stesso: ordine e caos sono indissolubilmente legati e costituiscono due diverse condizioni di un soggetto (il sistema dinamico) in continua evoluzione.

Semplicità e complessità
Il caos ci ha insegnato che sistemi che obbediscono a regole semplici possono avere comportamenti complicati. Eppure per molti aspetti il mondo ci appare semplice. Questa semplicità tende a sparire quando si esaminano le cose in profondità, ma in superficie tuttavia esiste. Per non correre il rischio, nel procedere dell'investigazione scientifica, di perdere di vista questa semplicità, recentemente si sta facendo strada un approccio diverso ai fenomeni naturali: la "teoria della complessità". Più che di un modello scientifico vero e proprio si tratta soprattutto di una filosofia che investe il modo di studiare i fenomeni in campi delle scienze molto vari, come ad esempio la teoria dell'informazione, la biologia o le scienze sociali.
Complessità può essere definita in generale come la proprietà di un oggetto che contenga informazioni difficili da ottenere. Questa definizione si declina in modi diversi nelle varie applicazioni, ma l'idea che sta alla base della teoria della complessità è che, a grandi scale, da interazioni complesse di un gran numero di componenti emergono concetti semplici. Questa idea scaturisce dalla constatazione che molti sistemi disordinati fuori dall'equilibrio possono auto-organizzarsi per dare origine a strutture ordinate. In questo senso si può dire che la complessità si situa in mezzo fra l'ordine e il disordine.

DINAMICA CAOTICA

Le leggi matematiche che generano i frattali sono molto semplici, pur tuttavia basta una minima variazione in un parametro per determinare una trasformazione significativa delle figure finali.

Variazioni nel triangolo di Sierpinski (al centro) al minimo variare di un solo parametro ma, attenzione, questo non è il caos!

Si usa dire che l'aspetto di un oggetto frattale dimostra un'estrema sensibilità alle condizioni di partenza che usiamo per costruirlo: nel caso del triangolo di Sierpinski, che è generato da un'equazione di primo grado, tuttavia, si riconosce sempre la forma iniziale. Invece i frattali generati da equazioni almeno di secondo grado  sono esempi tipici di sistemi caotici.

La parola caos richiama alla mente uno stato di totale disordine e si usa per indicare appunto tutte quelle situazioni nelle quali non si riesce ad individuare una regola.
"...a quegli spari successe il caos, e nessuno capì più nulla..." recita il Manzoni.
Del resto già gli antichi greci chiamavano caos la materia primordiale senza ordine che preesisteva al cosmos, cioè all'universo ordinato.

Precipitare nel caos sembra quindi finire in un mondo senza leggi, senza sicuri sviluppi, nel mondo della casualità: tutto l'opposto, quindi, di ciò che siamo abituati a ricomprendere nell'ambito della scienza.
Così riconosciamo ordinato il mondo della natura quando possiamo predire con millimetrica precisione non solo la data della prossima eclisse ma anche la zona dove si potrà ammirare meglio lo spettacolo; se la scienza non sa darci risposte esatte in alcuni casi, immaginiamo che questo accada perchè le leggi che governano certi fenomeni sono troppo difficili per essere comprese dall'uomo almeno fino a questo momento. (Come diceva Bertrand Russel, filosofo del nostro secolo, le leggi della Natura sono semplici perchè non siamo capaci di scoprire quelle difficili...).
In effetti, il metodo adottato dalla scienza classica tende a trascurare tutti quei fenomeni che non possono essere previsti esattamente, relegando nella sfera del disordine certe turbolenze o irregolarità che pure spesso convivono nella realtà di tutti i giorni.

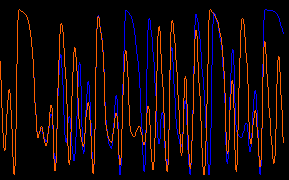
Facciamo un esempio: se gettiamo due barchette una accanto all'altra in un fiume che scorre lento e placido, esse rimarranno a lungo vicine, e subiranno la stessa sorte; se però il corso d'acqua si trasforma in una rapida, la loro rotta non sarà prevedibile e molto probabilmente le barchette potranno trovarsi lontane. Nell'immagine a lato, è rappresentato il moto di due barche (uno in rosso e l'altro in blu). All'inizio i moti si sovrappongono, e infatti si vede soltano la linea rossa, poi invece spesso prendono direzioni del tutto diverse. Questo significa che, a partire dalla stessa posizione iniziale, la posizione successiva non è predicibile. Perchè? Forse che la turbolenza porta con sé il caso? E' qui che entra in gioco la teoria del caos, intesa in senso moderno, matematico.

L'attuale definizione di caos è tutta qui: "la sensibilità alle condizioni di partenza". Ma cerchiamo di spegarci meglio.

Le leggi della natura permettono di predire con sicurezza molti fenomeni naturali: dal ritorno delle comete alle eclissi, alle mareee.
Alcuni aspetti della realtà sono però molto difficili da descrivere e da interpretare. Le condizioni atmosferiche, ad esempio, diventano imprevedibili a lungo termine, perchè ogni piccola variazione nelle condizioni attuali si amplifica e si ingigantisce in breve tempo: tutto questo anche se l'atmosfera ubbidisce a leggi fisiche ben precise che esprimono, ad esempio, il legame fra pressione e temperatura, fra pressione e velocità del vento e così via.

Questa sensibilità alle condizioni iniziali è detta effetto farfalla, da quando, nel 1972, il meteorologo Edward Lorenz raccontò, per illustrare la difficoltà di predire a lungo termine certe turbolenze climatiche, di come sia possibile, teoricamente, che un battito d'ali di una farfalla in Brasile provochi un tornado in Texas.
Che cosa intendeva dire in realtà?
Edward Lorenz, meteorologo presso il MIT (Massachusetts Institute of Technology), aveva sviluppato al computer un modello delle condizioni atmosferiche. Anche se i suoi risultati non erano utili per le previsioni del tempo reale, tuttavia erano realistiche nel riprodurre la sua variabilità , e in particolare nel non presentarsi mai in aspetto identico a se stesso. Nel 1961, avendo fretta, inserì nel suo computer dei numeri approssimati a tre cifre decimali invece che a sei come faceva di solito. Ora, ci si aspetta che se le condizioni iniziali sono approssimativamente simili , e si seguono le leggi naturali, anche il comportamento finale non varia di molto. Senza questa regola, la fisica non avrebbe fatto grandi passi avanti, perchè spesso la realtà è talmente complicata che occorre trascurarne vari aspetti.
Quello che apparve agli occhi di Lorenz fu invece una parte simile, ma una parte totalmente diversa. Dopo un iniziale smarrimento, egli si era reso conto che sebbene i frattali non presentino la stessa turbolenza di un uragano, essi tuttavia costituiscono un buon modello per lo studio di molte perturbazioni, proprio per la loro dinamica caotica.

Frattali e Caos

E' straordinario il fatto che i frattali dedotti da algoritmi cosi' semplici, mostrino delle forme cosi' complesse e cosi' somiglianti a cio' che vediamo in natura.

Tutto questo e' solo un caso o c'e' qualcosa di piu' profondo?

Una possibile spiegazione e' che la Natura si comporti come un computer, con delle leggi che non sono altro se non l'esecuzione di algoritmi. Inoltre, tra gli infiniti algoritmi possibili,sono preferiti quelli piu' semplici simili a quelli che producono i frattali.

Dicendo che la Natura e' un computer, non vogliamo dire altro se non qualcosa di risaputo e cioe' che le leggi della natura sono leggi matematiche. Infatti i programmi di computer non sono che matematica in azione.

Possiamo pensare allo scienziato come qualcuno che fa delle misure e poi cerca di trovare degli algoritmi che riproducono queste misure e permettono di prevedere il risultato di misure future.

Ora in natura si ritrovano assieme numerose simmetrie e il caos. Ma finora gli scienziati non sapevano dare ragioni valide per tutto questo.

Se ci riferiamo alle leggi di natura come programmi di computer la cosa si "spiega". Sembrerebbe che se ci sono due programmi possibili per regolare un certo fenomeno, il padreterno come quasi tutti i programmatori preferisce il programma piu' corto.(Chi e' programmatore sa che per tenere piccolo un programma bisogna usare dei cicli e che un ciclo puo' essere a sua volta realizzato da una procedura ricorsiva.)

I programmi piu' corti possibili sono quelli contenenti procedure ricorsive. Sono queste procedure ricorsive a generare delle simmetrie spaziali.

Vedi per esempio la costruzione di un albero.

Un albero e' definito disegnando il tronco; girandosi a destra e disegnando un altro albero piu' piccolo, poi a sinistra e disegnando un secondo albero uguale.

Certo direte non e' un albero realistico. Eppure con un algoritmo solo poco piu' complicato, sono riusciti a sintetizzare numerose piante in 3D uguali a quelle reali.

Insomma simmetrie spaziali e frattali (che sono simmetrici rispetto al cambiamento di scala) si presentano ogni volta uno vuole risparmiare sull'algoritmo usando una procedura ricorsiva.

Che dire del caos?

Se ci riferiamo a fenomeni fisici nel tempo (cioe' al loro andamento temporale) essi saranno descritti da una o piu' variabili. Per non complicare le cose, usiamo una sola variabile x. Il piu' semplice algoritmo che descrive l'andamento temporale di questa variabile e' come al solito una procedura ricorsiva ma questa volta in termini temporali: x(t+1) = f(x(t)).

Questa e' quella che in gergo viene chiamata iterazione.

Per modellare fenomeni naturali siamo interessati a iterazioni non banali come quelle che fanno diventare x costante, ne' impossibili come quelle che fanno diventare x infinito.

La piu' semplice iterazione non banale e' x = c*x*(1-x).

L'andamento di questa iterazione varia al variare del valore iniziale x₀.Il diagramma di Feigenbaum, da a colpo d'occhio cosa succede al variare di x₀. Prima si stabilizza su un unico valore, poi comincia a ciclare tra 2, poi 4, 8,16, e infine infiniti valori, cioe' diventa caotica!

Cioe' la necessita' di avere un programma piccolo ha come conseguenza delle leggi realizzate da iterazioni, e queste presentano un andamento caotico.

Forse bisognerebbe spiegare meglio da dove viene questo andamento caotico.

In matematica esiste questa astrazione che sono i numeri reali:astrazione perche' essi hanno precisione e informazione infinita e percio' sono impossibili da realizzare nella vita reale.

Infatti i numeri risultato di misurazioni, sono di necessita' finiti come lo sono i numeri cosiddetti reali nel calcolatore.

I matematici e i fisici, non si erano resi conto che questa piccola differenza puo' provocare il caos.

Da notare che questo tipo di caos prodotto da algoritmi semplici non va confuso col caso dove non esistono algoritmi per riprodurre i risultati osservati:ad esempio i risultati del lotto. Per distinguere i due casi si parla di caos deterministico quando esso e' prodotto da leggi semplici e di "caso" quando l'unico algoritmo possibile e' quello di enumerare tutti i risultati ottenuti senza che sia possibile prevedere quelli futuri.

Il fatto che il caos sia possibile con leggi semplici e' stata una grande scoperta ed ha fatto sperare che alcuni fenomeni finora considerati casuali (cioe' impossibili da descrivere se non con leggi statistiche) siano in effetti dovuti a leggi semplici (ad esempio l'andamento della Borsa).

Ce ne siamo resi conto col calcolatore che usa numeri approssimati come la realta'.

Ma cosa succede con esattezza?

Supponiamo prima di usare numeri ideali . A ogni numero reale di partenza per l'iterazione corrisponde una sequenza di numeri ideali e questi formano la sua orbita.

Immaginiamo di conoscere tutte queste orbite.

Ora uso il mio limitato calcolatore (o le misure reali) e dopo il primo passo, il risultato e' gia' un'approssimazione e quindi invece di continuare sull'orbita di partenza salto per cosi' dire su un'altra orbita. Cosi' a ogni passo.

Se l'iterazione si comporta bene posso finire vicino a dove sarei finito nel caso ideale, ma nel caso del caos, vado a finire da tutt'altra parte!

In effetti la firma del caos e' nel fatto che prendendo un certo numero di punti di partenza molto vicini, si vede che questi dopo un po' di tempo si sono sparpagliati per tutta una regione dello spazio, che' e' l'attrattore strano per quella iterazione.

Di solito un attrattore strano e' un frattale. Per cui il modo piu' semplice per disegnare un frattale e' attraverso un'iterazione di 1,2,3 o piu' parametri.

Ad esempio l'attrattore di Lorentz e' creato da una iterazione a 3 parametri, che doveva servire a modellare il tempo atmosferico.

I fenomeni nonlineari o con feedback in natura, sono quindi dovuti alla "necessita'" di dover usare algoritmi semplici e percio' ricorsivi.

Da notare che molto prima della scoperta del caos deterministico , si usava il computer per generare "numeri a caso"(in realta' sequenze periodiche molto lunghe perche' prima o poi gli stessi numeri devono ripetersi) con iterazioni. La piu' usata e'

x = resto della divisione di (x*m+p) e q.
ma nessuno aveva pensato che questo potesse avere un significato cosi' profondo.

Gli insiemi di Julia e Mandelbrot sono legati alle iterazioni nel modo seguente.

Volendo approfondire lo studio matematico delle iterazioni conviene passare da iterazioni reali come la x = c*x*(1-x) a iterazioni complesse z = c*z*(1-z) dove c e z sono complessi.

Nel campo complesso si vede che esiste un'iterazione ancora piu' semplice z = z^2 + c che e' caotica! percio' conviene cominciare da questa.

Volendo studiare questa iterazione, vediamo che dipende da quattro parametri: due x0,y0 sono il punto di partenza,gli altri c1,c2 sono la costante.

Possiamo tenere c1 e c2 costanti, facendo variare x0,y0 e rappresentando il fatto che l'iterazione va o meno all'infinito:questo e' l'insieme di Julia.

Per ogni c si ha un diverso insieme.

Viceversa possiamo tenere x0,y0 costante e uguale a 0, e variare c, ottenendo l'insieme di Mandelbrot. (Anche qui potremmo avere piu' insiemi ma in effetti gli insiemi per x0,y0 diverso da 0, sono identici a quello a 0 a parte delle deformazioni.)

Come si vede questa e' una generalizzazione del diagramma di Feigenbaum, e non c'e' da meravigliarsi che siano cosi' complessi e cosi' simili a scenari naturali, perche' sono legati a iterazioni che descrivono fenomeni naturali.

Questi insiemi di julia, mandelbrot e il diagramma di Feigenbaum si possono definire per ogni possibile iterazioni, ed hanno di solito caratteristiche molto simili a quelli prototipici dell'equazione logistica e della mappa quadratica.

Tenuto conto della potenza delle funzioni ricorsive nel generare pattern naturali,ci si chiede se non sia possibile trovare un sistema generale per sintetizzare immagini naturali. Ebbene si, sono stati trovati almeno due metodi che partono ambedue dalle funzioni ricorsive.

Nel primo metodo, della grammatica di Lindemeyer, partiamo dalla constatazione che l'effetto finale di una chiamata ricorsiva e' di generare una stringa di move e turn che alla fine sono trasformati in disegno. Assegnamo a questi dei simboli che saranno quelli base nella nostra grammatica. Quindi definiamo dei simboli complessi e delle regole che ci dicono come i simboli complessi possono trasformarsi in simboli complessi e simboli base. Con questa grammatica, facciamo un certo numero di iterazioni,generando a partire da una stringa iniziale, una stringa finale. Questa sara' poi interpretata dalla tartaruga che disegnera' solo i simboli base. Questo approccio puo' essere esteso anche a 3 dimensioni con una tartaruga "3D" e porta a realistiche simulazioni di piante ma anche di altri oggetti.

Nel secondo metodo,si tiene conto del fatto che se, una procedura ricorsiva richiama se stessa ad esempio tre volte, quello che succede e' che dei punti di una figura, vengono sottoposti nelle diverse generazioni a 3 differenti trasformazioni che li trasformano in tre figure ruotate, scalate e translate. Si tratta in effetti di trasformazioni affini e un insieme di trasformazioni affini assieme a una figura di partenza e' equivalente al programma ricorsivo originale. Ma possiamo andare oltre e chiederci se esiste una iterazione che abbia come attrattore la figura originale. La risposta e' si. Basta usare il sistema nel modo seguente: si parte da un punto qualsiasi,poi a ogni iterazione si sceglie una trasfromazione affine a caso e la si applica. Questo e' il cosiddetto algoritmo del caos di Barnsley. Il risultato finale (dopo molte iterazioni) e' la figura originale!

Ci si chiede se non e' possibile in questo modo sintetizzare qualsiasi immagine. Ebbene anche qui la risposta e si'! Barnsley ha mostrato una procedura per ricostruire a partire da un'immagine il sistema che lo sintetizza. Non e' facile, ma se uno ci riesce puo' comprimere l'immagine originale rappresentandola coi pochi numeri del sistema. E' questo il metodo di compressione coi frattali.

Ora il cerchio e' chiuso! Siamo partiti dalla constatazione se la suggestiva somiglianza dei frattali con scene naturali non abbia qualche significato,e siamo giunti alla conclusione che sia possibile modellare la realta' o almeno la sua immagine con dei frattali.

Applicazioni

La scoperta del caos deterministico in fisica ha prodotto una vera e propria rivoluzione, le cui idee risultano così efficaci per il comportamento di certi sistemi della fisica che si è pensato potessero funzionare da metafora per i fenomeni biologici  ed anche per il comportamento e la mente dell'uomo.
Improvvisamente nell'osservazione del mondo, le somiglianze divengono più importanti delle differenze.
Il caos è più fondamentale dell'ordine. E' la situazione più comune in Natura, mentre l'ordine è relativamente raro e può essere facilmente distrutto dalla più piccola perturbazione.
La Natura stessa usa il caos come parte integrante del suo programma di evoluzione. Per risolvere il problema di adattare le forme di vita per la sopravvivenza in un ambiente in continua trasformazione, complesso, apparentemente caotico, ogni schema deterministico sarebbe destinato al fallimento.
Perciò la Natura sceglie di combattere il caos con il caos, generando una moltitudine di forme di vita attraverso le mutazioni casuali.

La teoria del caos suggerisce che non si possono sempre prevedere gli effetti a lungo termine delle nostre creazioni e che è quindi meglio essere aperti e flessibili. Così come la natura sopravvive grazie alla biodiversità, è fondamentale avere una varietà di idee e di approcci. Quando si chiude una via, la natura ha molte altre strade tra cui scegliere. Ciò dovrebbe insegnare alle organizzazioni che una eccessiva specializzazione porta alla morte.

Ebbene, è possibile che a questo punto qualcuno si domandi  in che modo, nella pratica, sono stati utilizzati tali principi. Si espongono alcuni esempi, pertinenti a diversi ambiti di studio:

I sistemi biologici

Fino a 20 anni fa gli specialisti dei diversi settori erano convinti che i sistemi biologici potessero avere una sola soluzione: tendere verso uno stato di equilibrio e, di conseguenza, la presenza di fluttuazioni disordinate, imprevedibili, caotiche veniva attribuita a cause esterne o patologiche, eccezionali, normalmente assenti; in medicina, ad esempio, si ipotizzavano errori nella recessione del numero di casi di una malattia, crisi epilettiche, aritmie cardiache, e così via. Da circa 20 anni si è cominciato a pensare che queste variazioni "caotiche" possono essere inerenti ai sistemi, ovvero contenute nei modelli teorici deterministici che descrivono l'evoluzione dei sistemi stessi. Questo nuovo modo di pensare ha portato a risultati insospettati.

Nel campo della fisiologia cardiaca

Secondo esperti della Harvard Medical School, il caos procura al corpo umano una flessibilità che gli permette di rispondere a stimoli diversi. Si considerino ad esempio le proprietà elettrofisiologiche del cuore. Come è noto, la funzione fisiologica del cuore è di pompare sangue in tutto il corpo. Perché questo accada un'eccitazione elettrica, che origina in zone specializzate del muscolo cardiaco, si diffonde in tutto il miocardio attivando così la contrazione muscolare. Nel campo della fisiologia cardiaca  recentemente è stato introdotto l'impiego di tecniche di analisi spettrale ed è solo da un decennio che la dinamica non lineare e la teoria del caos sono state riconosciute come estremamente promettenti e impiegate in studi cardiologici.
Insomma ci si avvale degli strumenti delle scienze fisico-matematiche, talché sembra prendere più corpo l'ipotesi che è il normale ritmo cardiaco ad essere caotico e non la fibrillazione!
Questa affermazione prende lo spunto teorico dal fatto che il sistema di generazione del ritmo cardiaco è formato da un oscillatore periodico controllato da una molteplicità di meccanismi non lineari (ormoni, sistema simpatico e parasimpatico...).
Si è confrontato per esempio lo spettro di frequenza di un elettrocardiogramma di soggetti normali e di soggetti malati di cuore. Si è osservato che gli ECG dei primi presentano delle irregolarità su scale che vanno da qualche secondo a qualche giorno, mentre quello dei pazienti presenta uno spettro molto più piatto. Per esempio, si è osservato che alcune persone molto malate hanno dei battiti molto regolari prima di morire.
Infatti il ritmo cardiaco si deve adeguare all'attività dell'organismo (respirazione, attività mentale, ecc.). Questo aggiustamento produce un ritmo irregolare.
In alcune malattie il cuore perde la capacità di adattarsi all'attività dell'organismo e perciò presenta un ritmo estremamente periodico.
Un'importante lezione che dobbiamo trarre da questa rivoluzione scientifica è che leggi semplici non portano necessariamente a comportamenti semplici.  

Nelle relazioni umane:

Uno schema di sistemi non-lineari, ad esempio può essere rappresentato nel modo in cui una donna può impegnarsi in una serie di disastrose relazioni con uomini simili, oppure nel modo in cui un uomo sembra sempre entrare in conflitto con figure autorevoli.
Questo non vuol dire che il comportamento sia causalmente determinato, ma che il modo in cui la personalità si è strutturata in sistema aperto nel contesto di una più vasta società conduce ad una serie di schemi ricorrenti.

L'attività cerebrale

Si sono compiuti esperimenti registrando l'attività cerebrale di soggetti umani mentre affrontano determinati problemi. E' stato scoperto che questa complessività si modifica in funzione dell'attività cognitiva e che le forme più complesse degli EEG corrispondono agli stati mentali di maggior stato di allerta.