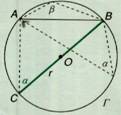
Teorema della corda - Teorema di Carnot

matematica

Teorema della corda

Per dimostrare indichiamo con G la circonferenza, r il raggio, O il centro, AB una corda di, a e b due angoli alla circonferenza che sono sottesi dalla corda AB e hanno vertice d 646f58g a parti opposte di AB.

Ci riconduciamo a un teorema sui triangoli rettangoli tracciando, il diametro BC. Riconoscendo nella corda AB un cateto del triangolo rettangolo ABC, scriviamo la relazione:

AB = BC sena = 2r sena

Poiché b = p - a vale anche: 2r senb = 2r sen (p -a) = 2r sena = AB

Sintetizzando in una formula:

AB = 2r sena

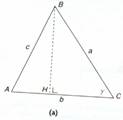
Teorema di Carnot

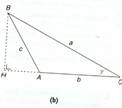
Applicare il teorema di Pitagora al triangolo rettangolo AHB, ottenuto proiettando B sul lato opposto in H. Vale che:

AB² = HB² + AH² = (a seng + (b - a cosg)² = a² sen²g + b² + a² cos²g - 2ab cosg = a² (sen²g + cos²g) + b² - 2ab cosg = a² + b² - 2ab cosg

Teorema dei seni

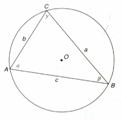
Inscritto il triangolo in una circonferenza, I lati ne sono corde e gli angoli di vertici A, B, C sono angoli alla circonferenza.

Applico il teorema della corda

così via fino ad ottenere la formula.