|
|
| |
a: ipotenusa b: cateto c: cateto
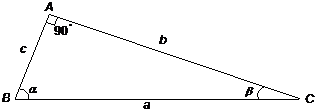
![]()
![]()
![]()
In un triangolo rettangolo la misura di un cateto Ŕ uguale a quella dell'ipotenusa moltiplicata per il seno dell'angolo opposto al cateto o per il coseno dell'angolo acuto adiacente al cateto stesso:
![]()
![]()
|
DEFINIZIONE |
FORMULA |
|
In un triangolo rettangolo la misura dell'ipotenusa Ŕ uguale al rapporto tra la misura di un cateto e il seno dell'angolo opposto al cateto o il coseno dell'angolo acuto adiacente allo stesso cateto. |
|
|
Il seno di un angolo acuto di un triangolo rettangolo Ŕ uguale al rapporto tra il cateto opposto e l'ipotenusa. |
|
|
Il coseno di un angolo acuto di un triangolo rettangolo Ŕ uguale al rapporto tra il cateto adiacente e l'ipotenusa. |
|
In un triangolo rettangolo la misura di un cateto Ŕ uguale a quella dell'altro cateto moltiplicata per la tangente dell'angolo opposto al primo o per la cotangente dell'angolo acuto adiacente, sempre, al primo cateto:
![]()
![]()
|
DEFINIZIONE |
FORMULA |
|
La tangente di un angolo acuto di un triangolo rettangolo Ŕ uguale al rapporto tra il cateto opposto e il cateto adiacente all'angolo considerato. |
|
|
La cotangente di un angolo acuto di un triangolo rettangolo Ŕ uguale al rapporto tra il cateto adiacente e il cateto opposto all'angolo considerato. |
|
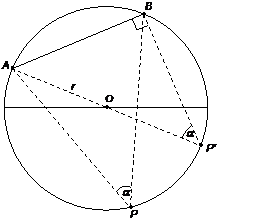 La
misura di una corda circonferenza Ŕ uguale al prodotto della misura del
diametro per il seno di uno qualunque degli angoli alla circonferenza che
insistono su uno dei due archi sottesi dalla corda.
La
misura di una corda circonferenza Ŕ uguale al prodotto della misura del
diametro per il seno di uno qualunque degli angoli alla circonferenza che
insistono su uno dei due archi sottesi dalla corda.
![]()
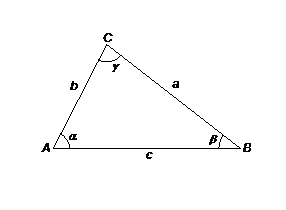 In
un triangolo qualunque la misura di un lato Ŕ costante il rapporto tra la
misura di un lato ed il seno dell'angolo.
In
un triangolo qualunque la misura di un lato Ŕ costante il rapporto tra la
misura di un lato ed il seno dell'angolo.
![]()
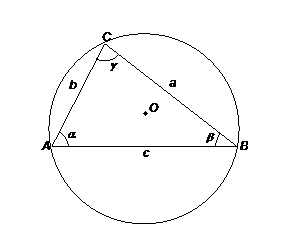 Il
valore comune dei suddetti rapporti Ŕ anche uguale alla misura del diametro
della circonferenza circoscritta al triangolo.
Il
valore comune dei suddetti rapporti Ŕ anche uguale alla misura del diametro
della circonferenza circoscritta al triangolo.
![]()
In un triangolo qualunque, il rapporto tra due lati Ŕ uguale al rapporto tra i seni degli angoli opposti ai lati considerati.
![]()
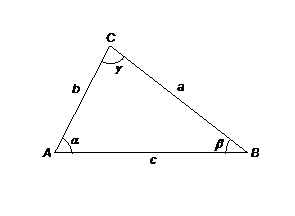 In
un triangolo qualunque, il quadrato della misura di un lato Ŕ uguale alla somma
dei quadrati delle misure degli altri due diminuita del doppio prodotto di
queste due per il coseno dell'angolo opposto al primo lato.
In
un triangolo qualunque, il quadrato della misura di un lato Ŕ uguale alla somma
dei quadrati delle misure degli altri due diminuita del doppio prodotto di
queste due per il coseno dell'angolo opposto al primo lato.
![]()
In un triangolo qualunque la somma di due lati (diversi tra loro) sta alla loro differenza come la tangente della semisomma degli angoli opposti ai suddetti lati sta alla tangente della loro semidifferenza.
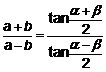
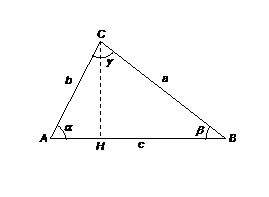 In
un triangolo qualunque la misura di un lato Ŕ uguale alla somma dei prodotti di
quelle degli altri due lati per il coseno dell'angolo che ciascuno di questi
forma col primo:
In
un triangolo qualunque la misura di un lato Ŕ uguale alla somma dei prodotti di
quelle degli altri due lati per il coseno dell'angolo che ciascuno di questi
forma col primo:
![]()
![]()
![]()
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025