Serie

Teorema di Abel

Sia una serie di potenze. Allor 313c25d e r : 0 <= r <= , detto raggio di convergenza della serie con le seguenti proprietà:

la serie converge assolutamente "z I(z₀, r) e uniformemente, preso R : 0 <= R <= r "z I(z₀, R);

la serie data diverge "z : z - z₀ > r

"z I(z₀, r) la somma della serie è una funzione analitica, tutte le derivate si ottengono derivando termine a termine, e le serie derivate hanno lo stesso raggio di convergenza r

se , allora .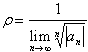

Teorema

Sia (f, W) un elemento analitico, e sia z₀ W. Sia W_z0 il più grande cerchio aperto di centro z₀, la cui circonferenza g sia tutta in W. Allora "z W_z0

è lo sviluppo di Taylor.

DIM.:

f, per ipotesi, è analitica si g. La formula integrale di cauchy permette di scrivere i valori di f(z) su W_z0 noti gli f(w) su g

e si scrive 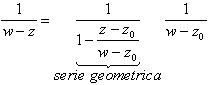da cui 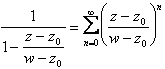e sostituendo

.

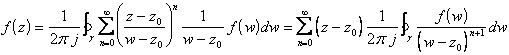Si osserva che

.

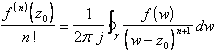Teorema

Sia W la corona circolare aperta di centro z₀ C e raggi r e R, cioè W = e sia (f, W) un elemento analitico. Allora, "z W si ha:

con

con g ciclo percorso una sola volta in senso antiorario, contenente z₀ e contenuto tutto nella corona.

DIM.:

Si pratichi un taglio che colleghi le due circonferenze in modo che W sia semplicemente connessa. Si applichi la formula di Cauchy

in cui sono stati eliminati i contributi dovuti al taglio. Su g_R si ha da cui

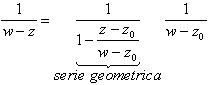da cui 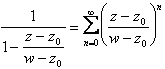e ci si riconduce a quanto detto per lo sviluppo di Taylor.

Per g_r si ha e allora si ricava

da cui .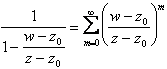

In modo simile al precedente si ottiene una sommatoria che varia da - a -1, e riunendo il risultato si ottiene la tesi.

Zeri e principi di identità

Sia (f, W) un elemento analitico. Sia z₀ W tale che f(z₀) = 0 ed n per cui f⁽ⁿ⁾(z₀) è la prima derivata non nulla, ovvero si ha uno zero di ordine n. Allora f(z) = (z - z₀)ⁿg(z) con g(z) analitica e non nulla in z₀ e z₀ è uno zero isolato

DIM.:

Si sviluppi in serie di Taylor

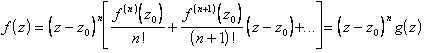
essendo g(z) analitica e per di più .

Poichè g(z₀) U_z0 : "z U, g(z) 0. Dato che (z - z₀)ⁿ 0, segue che "z U, f(z) = (z - z₀)ⁿg(z) 0, cioè z₀ è zero isolato di f.

Teorema di annullamento

Una funzione analitica su W è sempre identicamente nulla se si annulla sopra una linea chiusa o un'area parziale contenuta in W

DIM.:

Sia C_z0,R il cerchio di raggio massimale in cui f è analitica. Siccome f è analitica in C_z0,R, si potrà sviluppare in serie di Taylor all'interno del cerchio. Segue che, "z C_z0,R per ipotesi sulle derivate. Si ha anche "z C_z0,R . per la dimostrazione completa si sceglie allora un punto z₁ . Si dimostra che f(z₁) = 0 allora il teorema è vero per l'arbitrarietà di z₁.

Si congiunga z₀ con z₁ tramite un arco di curva regolare. Si crei una successione di cerchi di raggio massimale con centri i punti z', z", ... appartenenti alla curva e soddisfacenti le richieste:

- z' : C'_z',r' abbia una parte non appartenente a C_z0,R;

- z" : C"_z",r" abbia una parte non appartenente a C'_z',r';

- etc.

Si deve dimostrare che f(z) = 0 in C'_z',r'. Infatti, siccome z₁ C_z0,R si ha che "n >= 0 f⁽ⁿ⁾(z') = 0. Allora lo sviluppo di f nel cerchio C'_z',r' darà

Si prosegue con lo stesso metodo e così si dimostra il teorema.