MATEMATICA - LE LINEE DI LIVELLO e GLI ESTREMANTI

matematica

MATEMATICA

LE LINEE DI LIVELLO e GLI ESTREMANTI

Questo argomento matematico viene applicato alla meteorologia in quanto, nella costruzione di mappe meteorologiche, le linee/curve di livello vengono disegnate per collegare, per esempio, i vari punti di uguale pressione (isobare) o di uguale temperatura (isoterme). In generale le curve di livello vengono utilizzate per rappresentare le funzion 959g62j i di due o più variabili. Prima di soffermarci sull'argomento principale, è meglio definire il significato di "funzione a due o più variabili".
Funzione di due variabili è una relazione che associa ad ogni coppia ordinata di numeri reali (x, y)   D uno ed un solo numero reale (ovviamente il tutto lo si può ampliare anche alle funzioni a più variabili):

f: D R dove D R² ;
(x, y) z = f (x, y)

Possiamo definire le curve di livello, come la proiezione ortogonale (perpendicolare) sul piano (x, y) dell'insieme E dei punti della superficie aventi lo stesso valore z = k, cioè con la stessa quota.

Un esempio: rappresentazione mediante linee di livello della funzione

z = 2x-y+1
le linee di livello sono rette di equazione: 2x-y+1=k che risultano parallele fra loro, in quanto hanno ovviamente lo stesso coefficiente angolare, in questo caso pari a 2.

La funzione avente la retta che passa per l'origine, avrà valore pari a 1, perché sostituendo a x e y della funzione i valori zero (coordinate dell'origine), si troverà 1.

f(0, 0) 2(0)-0+1 = 1
f(0, 2) 2(0)-2+1 = -1
f(3, 0) 2(3)-0+1 = 7

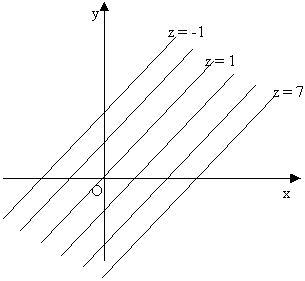
La funzione rappresenta un piano dello spazio che è intersecato dai piani z = k paralleli al piano xy secondo un fascio improprio di rette (è detto fascio improprio una serie di linee con direzione uguale) che è proiettato perpendicolarmente sul piano xy nel fascio di rette improprie di rette di equazione: mx+ny+p=k.
La rappresentazione mediante linee di livello viene utilizzata per la ricerca e la determinazione dei punti di minimo e massimo (relativi o vincolati). Si pensi, ad esempio, alle isoipse (le linee che congiungono le varie zone di uguale altezza) di una carta topografica o, nel caso di mappe meteorologiche, delle isobare, delle isoterme...

Ecco, invece, un esempio sulle modalità del calcolo di un minimo vincolato, che può essere risolto mediante: 1) rappresentazione grafica, 2) riduzione a una funzione di una variabile o 3) funzione di Lagrange.

Funzione obbiettivo: z = x²+y²
Vincolo tecnico: x+2y-4 = 0

1) Rappresentazione grafica

z = x²+y²

Si sostituisce alla z una variabile K:

k = x²+y²

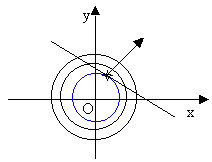
In questo caso, le linee di livello, sono una circonferenza di raggio k e di centro P(0, 0)
Con questo metodo bisogna studiare in quale modo cresca la funzione, tramite il metodo della sostituzione. I risultati dei calcoli di z(x, y) in due punti del piano, ci indicano il verso della "crescenza/decrescenza" della funzione stessa.

Funzione:
z(0, 0) 0+0 = 0
z(2, 2) 4+4 = 8
Quindi la funzione cresce dal centro verso la periferia.

Vincolo:
x 0   |   4
y 2   |   0


Da tutto ciò si evince che il punto tangente alla circonferenza di coordinate P(4/5, 8/5) è un minimo vincolato.

2) Riduzione a una funzione di una variabile

Si isola il vincolo e si determina la x.

x = 4-2y

Intersechiamo le due funzione (obbiettivo e vincolo) sostituendo la x nella funzione obbiettivo. Si ottiene, così, una funzione a una sola variabile.

z = (4-2y)²+y²
z = 5y²-16y+16

La condizione necessaria per la presenza di estremanti prevede che y'=o, quindi:

z'y 10y-16 = 0 per y = 8/5 z'>0 per y>8/5

Poi, per calcolare la x del punto (che può essere un minimo o un massimo), si sostituirà la y ottenuta al vincolo, per calcolare così il punto di minimo o massimo.
x = 4-2(8/5) 4/5
P (4/5; 8/5)

Per calcolare il valore della funzione in P(4/5; 8/5), si dovranno sostituire le coordinate del punto trovato alla funzione.

Zmin = (4/5)²+(8/5)² = 80/25

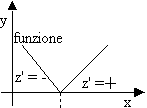
   ^{8/5 (min)}

3) Funzione di Lagrange

Si calcola, per prima cosa, la funzione lagrangiana (combinazione lineare della funzione obbiettivo e del vincolo):

zx = x²+y²+(x+2y-4)

Poi, per soddisfare la condizione necessaria per la presenza di minimi/massimi, si metteranno a
sistema le tre derivate delle variabili, ponendole uguali a zero.

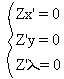
Quindi, applicando questo schema generale, all'esemplificazione in esame, otterremmo:

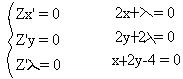
da cui = -8/5, y = 8/5, x = 4/5 quindi P(4/5, 8/5) e = -8/5

Questo per soddisfare la condizione necessaria per l'esistenza di minimi o massimi relativi; cioè, bisogna annullare le derivate prime parziali della lagrangiana, determinando poi il punto critico

P₀(x₀; y₀) e = ₀.

Poi bisogna calcolare l'hessiano orlato, per soddisfare la condizione sufficiente, mediante questo schema:



    0 g'x   g'y        0 1 2
H = g'x    z''_xx    z''_xy     1 2 0  =  -10
   g'y    z''_yx     z''_yy      2 0 2


       >0 massimo vincolato
se H    <0 minimo vincolato
       =    situazione indefinita (bisogna studiare localmente la funzione nell'intorno a P₀)

Quindi, essendo H<0, il punto in questione si tratta di un minimo vincolato.