Integrazione - Curve regolari

Un arco di curva regolare a tratti sarà l'insieme g di curve regolari g g_n tali che il punto finale di ciascuno coincida con il punto iniziale del successivo.

Un arco di curva regolare a tratti g rappresentato da z = f(t), t I = [a; b è detto chiuso se f(a) = f(b). Una curva regolare g è detta semplice se "t₁ t₂, f(t₁) f(t₂) eccetto al più per t₁ = a e t₂ = b. Una curva regolare chiusa e semplice sarà detta ciclo. g e -g rappresentano la stessa curva percorsa in senso opposto.

Una regione W si dice avere ordine di connessione n, ovvero n-planamente connessa, se la sua frontiera consta dell'unione di n curve chiuse. Per n = 1 la regione si dice semplicemente connessa.

Una regione di ordine di connessione n ha (n - 1) buchi.

Sotto condizioni molto generali, da una regione con ordine di connessione n si può ricavare, con (n - 1) tagli, una regione semplicemente connessa.

Integrazione lungo archi di curve regolar 515h73f i

Se f = u + jv è una funzione complessa continua di una variabile reale t, f : [a; b C, si definisce l'integrale di f su [a; b come

Sia f funzione complessa a valori complessi, definita su di un arco di curva regolare a tratti g. Sia z(t) = x(t) + jy(t), t [a; b una rappresentazione di g. L'integrale di f lungo g è per definizione

g si dice cammino di integrazione.

Siano f(z) e g(z) due funzioni complesse e continue di variabile complessa su di una curva regolare a tratti g. Allora:

;

;

Sia g g g , allora .

Sia g una arco di curva regolare a tratti e sia f(z) una funzione a valori complessi definita e integrabile su g, allora se in più "z g f(z) <= g(z) e g(z) <=M, detta L la lunghezza di g si ha

.

Questa equazione è detta equazione modulare.

DIM.:

"l C si ha . Per un numero complesso Re(z)<= z si ha . Quest'equazione è vera "l C, quindi ne posso scegliere uno opportuno. Si osservi che

e si scelga .

. Quindi .

Per definizione allora

. Con successive disuguaglianze fra integrali di funzioni reali, e allora .

Integrazione e funzioni analitiche

Teorema di Green

Sia W una regione del piano reale. Sia X(x, y)dx + Y(x, y)dy una forma differenziale su W, con X, Y di classe C¹. Sia S una parte di W, con contorno G costituito da un numero finito di curve chiuse regolari a tratti, e si prenda su tali curve come verso positivo quello che lascia S a sinistra. Allora

Sia W una regione del piano reale. Sia X(x, y)dz + Y(x, y)dy una forma differenziale su W con X e Y : W C di classe C¹. Allora sono equivalenti:

su W ;

"G W il cui interno è tutto in W si ha ;

"g g contenute in W con punti iniziali e finali coincidenti e che comprendano una parte di piano tutt contenuta in W si ha .

Sia f una funzione complessa di variabile complessa: l'integrale di linea = si riconduce all'integrale .

Sia W una regione di C. Sia f : W C = z = x + jy f(z) = f(x + jy) = u(x, y) + jv(x, y). Sono equivalenti:

f è analitica su W

f è differenziabile con derivate parziali continue ;

si ha anche e ;

con f continua, "G W chiusa il cui interno è tutto contenuto in W si ha la seguente uguaglianza ;

f è continua e comunque si scelgano du archi di curva regolari a tratti g g W racchiudenti S W si ha

Teorema di Cauchy

Sia f : W C analitica. Sia S W con contorno G appartenente a W, è costituito da un numero finito di curve chiuse regolari a tratti, e si prenda su tali curve come positivo il verso che lascia S a sinistra. Allora

DIM.:

Ci si riconduca al caso di una curva chiusa

La procedura dipende dal modo che si utilizza per trovare regioni semplicemente connesse a partire da regioni con ordine di connessione n praticando (n - 1) tagli.

La tesi del teorema di Cauchy vale anche se si suppone solo che f sia analitica su S e continua su G; non occorre che la curva G sia contenuta nella regione di analiticità, basta che f sia tutta o in parte sulla frontiera e vi ammetta limite continuo.

Teorema fondamentale del calcolo integrale per funzioni f : C C.

Sia f(z) : W C una funzione analitica su W semplicemente connessa. Allora fissato z₀ a "z, interno di W, la funzione è una primitiva di f(z) nel senso che "z W si ha F'(z)=f(z)

DIM.:

Per l'indipendenza dell'integrale dal cammino si ha: F(z + Dz) - F(z) =

;

preso il cammino che congiunge i due estremi com una retta, l'integrale di dw è Dz. Quindi , da cui

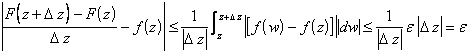
dalla quale segue che "z W si ha F'(z) = f(z).

Se f(z) è analitica si W semplicemente connessa e se F(z) è una sua primitiva, per ogni cammino che unisca z₁ e z₂ si ha:

DIM.:

Dalla definizione di primitiva dF / dz = f. Se G è anche primitiva di f, dG / dz = f. Segue cioè F - G = k. Da questa, che vale "z, si ricava che . Si riapplica il ragionamento per z₂ e quindi , ma per la precedente definizione di k si ha la tesi.

Sia f una funzione analitica in una regione W, sia W W tale che F sia analitica si W'. Si dice che F è estensione analitica di f a W' se F f "z W

Punti singolari e residui

Si è supposto che l'integrale di una funzione analitica su una regione non semplicemente connessa fosse sempre nullo, in realtà vanno aggiunti termini lungo i cammini che avvolgono i buchi. La presenza dei buchi ha molte conseguenze: può essere possibile estendere la funzione sugli stessi in modo da renderla analitica anche sui buchi, ma se questo non è possibile si è in presenza di punti singolari.

Si dice una funzione analitica globale l'unione di tutti gli elementi analitici ottenibili mediante prolungamenti successivi di uno stesso elemento analitico. Una f analitica si dice completa se non è estendibile.

Si chiama singolarità o punto singolare di un elemento analitico (f, W) un punto z₀ di W tale che non vi si possa estendere f.

Una singolarità si dice non isolata se in un qualunque intorno cade almeno un altro punto singolare, altrimanti è isolata.

Un punto singolare isolato si dice uniforme se si può ottenere un'estensione che non comprenda solo z₀. Negli altri casi si ha un punto di diramazione.

Sia z₀ singolarità isolata e uniforme di (f, W). E' un polo di ordine n si può scrivere , in cui h(z) è analitica e diversa da 0 in z₀.

Le singolarità uniformi che non sono poli sono dette singolarità essenziali.

E' evidente come per un polo di ordine n si abbia , mentre per le singolarità essenziali il limite non esiste.

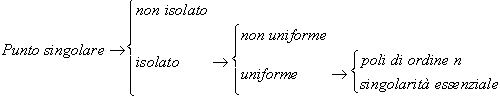
Dire che una funzione ha zeri di ordine n in z₀ equivale a dire che tutte le derivate sino alla (n - 1)esima sono nulle, e che la derivata n-esima è diversa da zero.

Sia z₀ in C una singolarità uniforme di una funzione analitica f. Sia g un ciclo racchiudente solo z₀ è tutto contenuto in W in cui f è analitica. Si dice residuo di f in z₀ e si indica con R_f(z₀) l'integrale

in cui il ciclo è percorso una sola volta in senso antiorario.

La precedente definizione non dipende da g

DIM.:

Siano g e g due curve chiuse avvolgenti z₀, tutte contenute in W e non intrecciantisi. La regiune racchiusa dalle due è una regione ad ordine di connessione 1. Da questa si può passare ad una regione semplicemente connessa praticando un taglio infinitesimo che unisca le due curve. La curva in cui t rappresenta il taglio non contiene singolarità. Allora

Teorema dei residui

Sia (f, W) un elemento analitico. Se il ciclo g racchiude n punti singolari isolati uniformi si ha:

DIM.:

Si considerino le curve g numerate da 1 a n e racchiudenti ognuna un punto singolare. Sia G l'unione delle precedenti con g. Allora

. Per il teorema di Cauchy

.

Se la funzione analitica f presenta un polo del primo ordine in z₀ ed è nella forma f(z) = h(z) / (z - z₀), allora

DIM.:

Sia j(z) la funzione ausiliaria definita come . Si deve dimostrare che R_j(z₀) = 0, poi, tramite l'additività degli integrali , ma , in quanto calcolato con la definizione, quindi R_f(z₀)=h(z₀).

in cui con R opportuno. Allora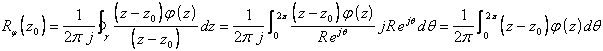

A cui posso applicare la disequazione modulare e la definizione di limite e da cui "e > 0 d > 0 tale che " z-z₀ < d si ha (z - z₀)f(z) - h(z₀) < e e, data la definizione di j, si ha (z - z₀)j(z)=(z - z₀)f(z)-h(z₀). Allora "e > 0 scegliendo R = d si ha che (z - z₀)f(z)-h(z₀) (z - z₀)j(z) < e e si conclude e cioè che il residuo di j è nullo.

Un criterio pratico per il calcolo del residuo di un polo semplice in z₀ è che se con n e d analitiche e n(z₀) 0, allora

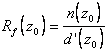
DIM.:

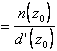
Formula integrale di Cauchy

Sia f analitica in una regione W. Sia g un cammino chiuso tutto contenuto in W e percorso una sola volta in verso antiorario. Sia S la regione racchiusa da g. Allora se w è un punto di g e z S si ha che "z S

DIM.:

Sia con w C. g(w) presenta al più un polo del primo ordine in w= z. Il residuo di g(w) in w = z è dato da

che è f(z).

Derivate successive di una funzione analitica

Sia (f, W un elelmento analitico, e sia g un ciclo contenuto in W. Allora "z g si ha

DIM.:

La si esegue per induzione completa.

Se esistono due valori successivi di n tali che la formula sia vera, basta che, supposta la formula vera per (n - 1), questa lo sia anche per n.

Se n = 0 allora , che è vera.

Se n = 1 si deve avere

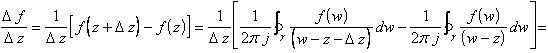
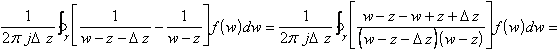
, da cui:

l'operazione di scambio degli operatori limite ed integrale è lecita per la continuità della funzione 1 / (w - z - Dz) rispetto a Dz;

.

Ora si supponga sia vera la formula per (n - 1). La si dimostra per n.

si ha

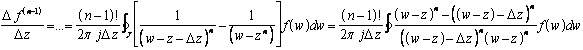
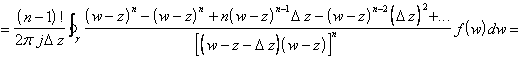
come in precedenza si applica il passaggio al limite e si invertono gli operatori. Si ottiene:

fine dell'induzione.

Sia (f, W) un elemento analitico e sia g una circonferenza di centro z e raggio r, tutta contenuta in W. Allora detto M l'estremo superiore dei valori di f(z) su g si ha:

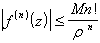
DIM.:

L'equazione di g è (z - z₀ = re^jq), da cui

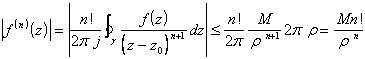
Teorema di Liouville

Se la funzione è analitica e limitata per ogni valore z C, allora f è una costante.

DIM.:

Poichè f è limitata "z C, M > 0 tale che f(z) < M "z C. Sia z un punto e sia g una circonferenza con centro in z e raggio r. Poichè f è analitica "z, per la precedente, con n = 1, si ha . Ma r è arbitrario, in quanto f è analitica in C, quindi f'(z) tende a zero quanto si vuole. Segue che f(z) è costante.

Teorema fondamentale sull'annullamento di un polinomio

Sia p una funzione polinomiale di grado n >= 1. Allora p(z) = 0 ha almeno una radice.

DIM.:

Se p non fosse mai nulla per z C, sarebbe analitica e non nulla "z C, inoltre siccome il limite tendente all'infinito di g è nullo, per Liuoville la p(z) sarebbe una costante. Ciò è assurdo.

Teorema fondamentale dell'algebra

In C, un polinomio di grado n ha esattamente n radici.

DIM.:

p(z) = 0 ha una radice z₀. Divido allora p(z) per (z - z₀) ed ho un polinomio di grado (n - 1) a cui applico lo stesso ragionamento. Ho allora

con n = n₀ + n₁ + ... + n_k.

Sia (f, W) un elemento analitico e sia z₀ un polo multiplo di ordine n. Allora

DIM.:

.

Decomposizione delle funzioni razionali

Una funzione razionale propria ha un numero finito di poli di ordine finito negli zeri z₁, z₂, ..., z_n di molteplicità n₁, n₂, ..., n_n, di d(z), si ha allora la seguente decomposizione in fratti semplici:

in cui, nei coefficienti A, il primo pedice rappresenta il polo che si considera e il secondo il grado.

, , ..., , oppure