FUNZIONI ELEMENTARI - LE POTENZE: RICHIAMI

a⁰ = 1 a^-1 = 1/a a¹ = a ^b√a = a^1/b

Usando le potenze possiamo costruire 2 diversi tipi di funzioni:

Le funzioni potenza y = x^b dove la variabile indipendente è la base, mentre l'esponente b è fissato;

Le funzioni esponenziali y = a^x dove la variabile indipendente è l'esponente, mentre la base a è fissata.

FUNZIONI POTENZA y = x^b

Le funzioni potenza con esponente positivo sono crescenti su (0; + ∞) e quindi conservano le diseguaglianze.

Le funzioni potenza con esponente negativo sono decrescenti su (0; + ∞) e quindi rovesciano le diseguaglianze.

Nei casi con esponente razionale b = m/n

Se m è pari, la funzione è pari ossia (- x)^b = x^b e il grafico è simmetrico rispetto all'asse y

Se anche m è dispari, la funzione è dispari ossia (- x)^b = - (x^b) e il grafico è simmetrico rispetto all'origine

FUNZIONI ESPONENZIALI

I grafici delle funzioni esponenziali sono solo di 2 tipi, a seconda che la base a sia <1 o >1:

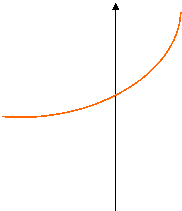
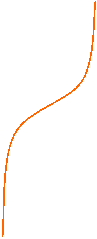
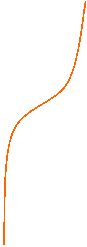
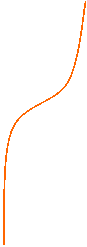
a > 1: il grafico passa per il punto (0; 1), è crescente e con la concavità rivolta verso l'alto.

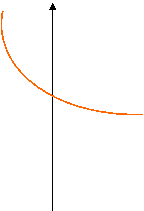
a < 1: il grafico passa per il punto (0; 1), è decrescente e convesso.

a > 1 0 < a < 1

1 1

LOGARITMI

Equazioni Logaritmiche: sono equazioni che contengono all'interno di un argomento di un log l'incognita x

Schema risolutivo:

Un solo log a dx e a sx.

Passare all'uguaglianza fra argomenti

Risolvere l'equazione e confrontarla con la C.E.

Le proprietà dei logaritmi:

log_a 1 = 0  poiché a⁰ = 1

log_a a = 1 poiché a¹ = a a^a = 1

c log_a b = log_a b^c

log_a (b  c) = log_a b + log_a c

log_a b/c = log_a b - log_a c

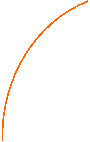
I grafici delle funzioni logaritmiche:

a > 1    0 < a < 1

crescente decrescente

1

TEOREMA DI RUFFINI

Esempio: x⁵ - 9x⁴ + 23x³ - 15x² < 0

x² (x³ - 9x² + 23x - 15) < 0

(polinomio) x³ - 9x² + 23x - 15 = 0

P(1) = 1 - 9 + 23 -15 = 0

1 - 9 + 23 -15

1 1 - 8 + 15

1 - 8 + 15 //

Risultato: x² (x² - 8x + 15) (x - 1) < 0

1 3 5

x² > 0 R

x² - 8x + 15 > 0 x < 3; x > 5

x - 1 > 0 x > 1

Soluzione: x < 1; 3 < x < 5

FUNZIONI TRIGONOMETRICHE E PERIODICHE

RICHIAMI DI TRIGONOMETRIA

Trigonometria: è lo studio delle relazioni che intercorrono tra le lunghezze dei lati e le ampiezze degli angoli di un  triangolo.

Radiante: è l'angolo che in una circonferenza è individuato da un arco lungo quanto il raggio.

Circonferenza trigonometrica: è la circonferenza del piano cartesiano di raggio unitario, con centro nell'origine.

Definizione: Dato un triangolo rettangolo OAB, retto in A, sia α l'angolo al vertice O.

Si dice coseno di α, in simboli cos(α), il rapporto tra la misura del lato adiacente OA e quella dell'ipotenusa OB.

Si dice seno di α, in simboli sin(α), il rapporto tra la misura del lato opposto AB e quella dell'ipotenusa OB.

Dal Teorema di Pitagora segue la seguente formula di identità trigonometrica fondamentale:

cos sin

Definizione: Sia α un qualsiasi n° reale e sia P il punto della circonferenza trigonometrica corrispondente ad un angolo di α radianti.

Si dice coseno di α, in simboli cos(α), l'ascissa di P.

Si dice seno di α, in simboli sin(α), l'ordinata di P.

sin

Si dice tangente di α, il rapporto tan

cos

cos

Si dice cotangente di α, il rapporto cot

sin

Mentre tan(α) e cot(α) possono assumere un qualsiasi valore reale, seno e coseno sono limitati:

seno coseno

-1 ≤ sin( ) ≤ 1 -1 ≤ cos(

(intervalli 1; -1; 1_ _ _) (parte da 1; -1; 1_ _ _)

1 1

-1 -1

sin(x)

tg( ) tg =

cos(x)

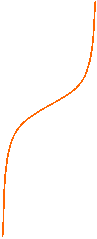
0 90° 180°