|
|
| |
MATEMATICA GENERALE
ESERCIZIO 2
Su una matrice A3x5 sono note le seguenti informazioni:
Determinare A e discuterne la caratteristica al variare di k. Nel caso essa sia minima, trovare una base per span(A) e per ns(A).
SVOLGIMENTO:
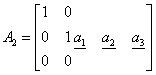
![]()
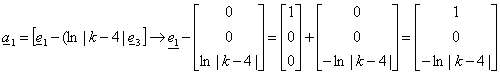
ns(B)=
![]()
a2 è un versore:
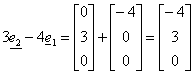
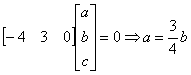
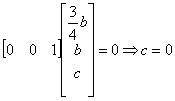
Ora applico la definizione di versore:
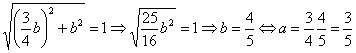
[ 1 2 3 4 5]
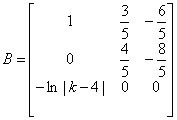 A
A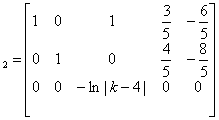
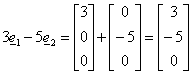
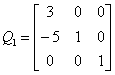
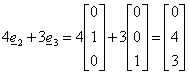
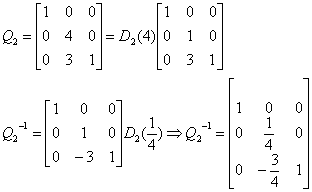
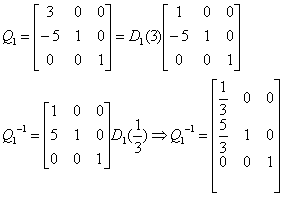
Se k=5 o k=3 (ln|1|=0) la pivotizzazione si arresta al secondo passo (r(A)=2) in quanto non esistono più pivot validi. In questo caso la caratteristica della matrice è minima.
Se k![]() 5 o k
5 o k![]() 3 potrà esserci un altro passo di pivotizzazione.
3 potrà esserci un altro passo di pivotizzazione.
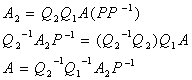
Non essendoci stati scambi sulla matrice, P=P-1.
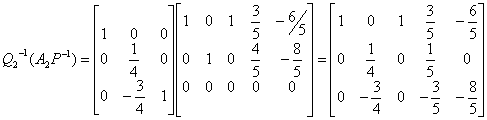
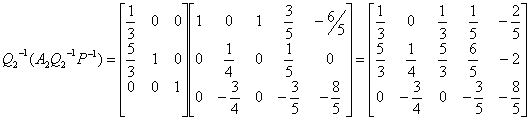
span: r(A)=2 quindi per la base servono due vettori linearmente indipendenti. Lo span di A è lo span di:
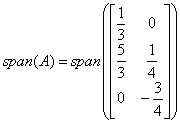
Utilizzo come span le prime due colonne perché, essendo pivotizzate, sono sicuramente linearmente indipendenti.
ns(A) Ax=0
A2x=0
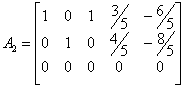
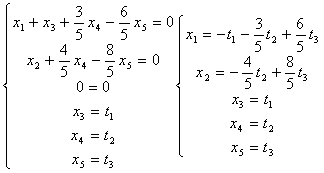
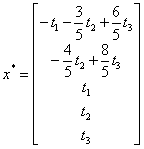
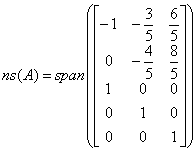
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025