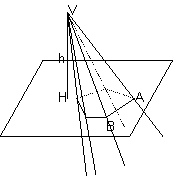Geometria solida - Piramidi rette

matematica

- Geometria solida -

Dicesi piramide la parte di angoloide compresa fra il vertice ed una sua sezione piana.

Il poligono sezione ne è la base

La distanza vertice-piano ne è l'altezza (VH)

I triangoli sezionati sulla faccia dell'angoloide sono le facce laterali. La loro area è la superficie laterale. Se aggiungo la superficie di base ottengo la superficie totale (S_T=S_L+S_B)

I lati delle facce laterali (VA,VB) e della base (AB) si dicono spigoli.

N.B.: in generale, VA VB.

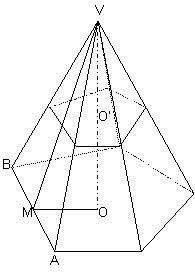Proprietà

Sia O il piede dell'altezza. Da esso traccia la perpendicolare ad uno spigolo di base (OM). VM è l'altezza del triangolo VAB.

Se sego una piramide con un piano parallelo alla base ottengo un poligono simile a quello di partenza.

I due perimetri quindi stanno fra loro come le rispettive distanze dal vertice, le aree con i quadrati delle distanze:

Piramidi rette

Tra le piramidi si distinguono le piramidi rette:

Una piramide si dice retta quando ha per base un poligono circoscrivibile ad un cerchio e l'altezza cade nel centro del poligono.

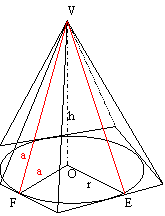Le altezze delle facce laterali di una piramide retta sono tutte uguali:

VE=VF=a

e il loro nome comune è apotema.

Vale la relazione pitagorica a²=r²+h²

Si osservi che solo le piramidi rette hanno l'apotema, le altre no.

Le piramidi rette, inoltre, hanno una formula facile per l'area:

cioè, l'area laterale è il perimetro di base moltiplicato per l'apotema e diviso per due.

Un caso particolare delle piramidi rette sono le piramidi regolari:

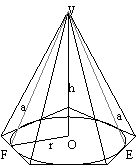una piramide retta si dice regolare se ha per base un poligono regolare.

Le facce laterali sono in questo caso triangoli isosceli uguali.

Il tronco di piramide

Il tronco di piramide è la porzione di una piramide compresa tra la base della stessa ed un piano parallelo.

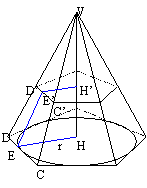
Tronco di piramide retta

Se il tronco si ottiene da una piramide retta, allora le facce laterali sono trapezi di uguale altezza (apotema).

L'area del tronco di piramide retta si ottiene con la seguente formula:

Cioè l'area laterale del tronco della piramide retta è data dal semiprodotto dell'apotema per la somma dei perimetri base.

NB:  si osservi, come per la piramide, che la formula 'semplice' dell'area totale vale solo per i tronchi di piramidi rette.

Tronco di piramide regolare

Le facce del tronco ottenuto da una piramide regolare sono trapezi isosceli regolari.