FUNZIONI

matematica

FUNZIONI

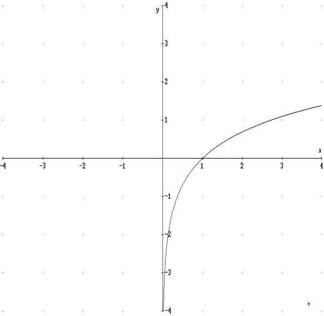
Passiamo ora ad un importante argomento che si caratterizza per la presenza di numerosi elementi dell'analisi matematica (derivate, limiti, campi di esistenza). Le funzioni altro non sono che dell 616b13g e curve le quali presentano caratteristiche diverse a seconda delle equazioni che le rappresentano. Ad esempio y=log x è una funzione logaritmo che presenta alcuni elementi base, utilizzabile anche nell'ambito di altre funzioni.

Lo studio di una funzione non è certamente una passeggiata!!!!, ma le difficolta' naturalmente possono variare in relazione al tipo di funzione studiata.

Ecco ora alcuni suggerimenti per affrontare in modo agevole (non perfetto), lo studio della funzione

Conoscenza delle principali funzioni elementari (spesso il grafico di altre funzioni si discosta poco da queste)

Affrontare dapprima il problema singolarmente e in seguito studiare interamente una funzione

Conoscenza della risoluzione di disequazioni ed equazioni di grado anche superiore al 2°

Conoscenza dei casi particolari che spesso facilitano lo studio della funzione (es. funzione omografica)

Dato qualche suggerimento passiamo ad elencare i punti base dello studio :

DETERMINAZIONE DEL CAMPO DI ESISTENZA DELLA FUNZIONE

DETERMINAZIONE DEGLI EVENTUALI PUNTI DI INTERSEZIONE CON GLI ASSI

RICERCA DEGLI ASINTOTI DELLA FUNZIONE (ORIZZONTALI, VERTICALI, OBLIQUI)

DETERMINAZIONE DEGLI INTERVALLI DOVE LA FUNZIONE CRESCE E DECRESCE, ATTRAVERSO LO STUDIO DELLA DERIVATA PRIMA DELLA FUNZIONE

DETERMINAZIONE DEI MASSIMI E DEI MINIMI DELLA FUNZIONE

DETERMINAZIONE DELLA CONCAVITA' E DELLA CONVESSITA' DI UNA FUNZIONE CON LO STUDIO DELLA DERIVATA SECONDA

RICERCA DEGLI EVENTUALI PUNTI DI FLESSO

RAPPRESENTARE GRAFICAMENTE LA FUNZIONE CON I DATI RICEVUTI DAI PRECEDENTI PUNTI