DEFINIZIONE DI INTEGRALE INDEFINITO

matematica

DEFINIZIONE DI INTEGRALE INDEFINITO

Sia f(x) una funzione definita in un intervallo A, la funzione F(x) si dice primitiva della f(x)

se, per ogni x di A, F(X) è derivabile e risulta

F'(x) = f(x)

Trovata una primitiva della funzione, tute le altre si ottengono aggiungendo una costante, 929f51j

ossia F(x) + c  esprime, al variare di c, tutte le primitive di f(x).

L'insieme formato da tutte le primitive di f(x), si chiama integrale indefinito della funzione f(x)

e si indica

La funzione f(x) si dice funzione integranda, dx indica la variabile rispetto alla quale si cerca la primitiva

Da quanto detto al punto 2. si ha

_{Da quanto detto al punto 1. si ha}

_{Integrale definito}

_{Sia f(x) una funzione continua nell'intervallo ]a,b[  F(x) una primitiva della f(x)}

_{si ha}

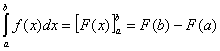
Questa formula è una conseguenza del teorema fondamentale del calcolo integrale (teorema di Torricelli)

viene chiamata formula di Newton - Leibnitz.

Dal punto di vista operativo, per calcolare l'integrale definito di una funzione f(x)

si deve determinare un integrale indefinito e calcolare la differenza tra i valori che l'integrale assume agli estremi dell'intervallo di integrazione

Significato geometrico dell'integrale definito

DERIVATE E INTEGRALI ELEMENTARI

Nella tabella si è messo in evidenza il legame tra derivata e integrale