Carica-scarica di un condensatore

fisica

Carica-scarica di un condensatore

Nel considerare circuiti RC (circuiti composti, oltre che da resistenze, da condensatori), si va incontro a correnti variabili nel tempo. Ci apprestiamo a studiare l'andamento della carica nel tempo all'interno di uno di questi circuiti.

Consideriamo il circuito rappresentato in figura:

							R

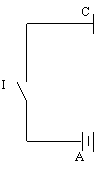
Esso e' costituito da un condensatore C, un generatore di forza elettromotrice f.e.m. (AB), una resistenza R ed un interruttore I.

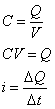
Prima di iniziare ricordiamo alcune relazioni fondamentali che riguardano condensatori, ddp, corrente.

(nota: C e' la capacita' esp 222d38c ressa in Farad, Q la carica espressa in Coulomb, V la tensione espressa in Volt, i l'intensità di corrente espressa in Ampere, t il tempo in secondi)

Chiameremo f la tensione fornita dal generatore. La carica accumulabile dal condensatore sarà il valore nominale fC.

Prendiamo in esame il circuito nelle sue condizioni iniziali e finali.

L'interruttore inizialmente e' aperto e la carica sulle armature del condensatore è 0. Chiuso l'interruttore, alla fine del processo di carica, si avrà sulle armature una carica fC.

Inoltre, in un generico istante, la corrente circolante nel circuito sarà:

Inoltre, nello stesso istante t, percorrendo il circuito in senso orario dal polo positivo A fino a tornare in A, considerando che il condensatore provoca una caduta di potenziale Q/C, per il principio di Kirchoff avremo:

Semplificando:

Ricordiamo che a noi occorre la funzione che esprima la carica Q in funzione del tempo. A questo punto è possibile calcolarla tramite calcolo integrale:

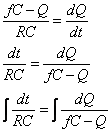
(nota: volendo si possono saltare questi passaggi e passare direttamente alla formula finale)

RC è una costante del circuito che chiameremo t e che possiamo portar fuori dal primo integrale:

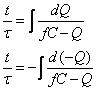
L'integrale di dt è proprio t, dunque:

Quindi, finalmente:

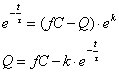
che, posta come uguaglianza di potenze di e, diventa:

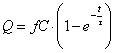
Per la determinazione della costante k di integrazione, consideriamo che nell'istante iniziale (t=0) la carica è nulla (Q=0). Appare subito evidente che k=fC.

Finalmente possiamo scrivere la funzione che esprime Q in funzione del tempo:

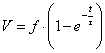
Da questa è immediato ricavare la funzione del potenziale V:

Le due funzioni sono dunque di tipo esponenziale. Per il tempo tendente ad infinito il condensatore dovrebbe assumere dunque la sua carica massima fC ma possiamo dire con buona approssimazione che il condensatore risulta carico già dopo 3 cicli t. Per t=3t infatti risulta:

Q= fC - e^-2 = fC - 0,1353.

A questo punto è doverosa un'osservazione. Ho scritto poc'anzi "t=3t". Se t è espresso in secondi, t indica dunque un tempo? Si! E la dimostrazione è abbastanza semplice:

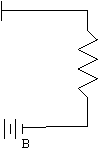
Un ragionamento analogo si segue per quanto riguarda il processo di scarica del condensatore. Stavolta prendiamo in esame un circuito ancora più semplice del precedente: vi è un condensatore C, già carico, collegato ad una resistenza R. E' evidente che appena colleghiamo il condensatore alla resistenza questo si scarica su di essa. Percorrendo il circuito in un generico istante t, avremo:

e considerando l'intensità istantanea come negativa (il condensatore si sta scaricando.) :

Da questa, per ricavare Q in funzione di t ricorriamo al calcolo integrale:

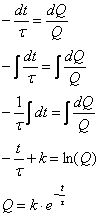
nuovamente poniamo la costante RC uguale a t

Determiniamo la costante k sapendo che all'istante iniziale (t=0) il condensatore è completamente carico (Q=Cf). Appare subito che k=Cf. Dunque la formula finale sarà:

dove f è la forza elettromotrice che genera il condensatore completamente carico. Seguono immediatamente la funzione del potenziale:

e quella dell'intensità di corrente:

Come si può vedere, anche in questo caso l'andamento della carica è esponenziale. Analogamente al processo di carica, il condensatore si può dire scarico dopo circa 3 cicli t. Per t=3t risulta infatti:

Q = Cf