ESPERIENZA DI LABORATORIO N.2 - URTI ELASTICI

In questa fase abbiamo utilizzato due alianti, il primo dei quali dotato di massa supplementare e anello avente massa M₂ = (1,5017 ± 0.0001) kg, il secondo costituito solo da anello con massa

M₁ = (0,9976 ± 0.0001) kg. Dopo aver messo in piano la tavola, abbiamo effettuato l'urto tra i due alianti riportando i dati ottenuti su un foglio di carta millimetrata sul quale abbiamo determinato i centri di massa del sistema dei due alianti. Per entrambi gli alianti abbiamo considerato 4 punti sperimentali A_i e B_i prima e dopo l'urto. Sappiamo che il centro di massa del sistema dei due alianti si trova sui segmenti che congiungono i punti individuanti le posizioni dei due alianti nello stesso istante di tempo. Per questo motivo le distanze dei generici centri di massa G_i dai punti sperimentali A_i , relativi all'aliante di massa maggiore, sono determinate mediante la seguente formula:

 

Prima dell'urto la distanza del centro di massa dal generico punto sperimentale è:

Dopo l'urto la distanza del centro di massa dal generico punto è:

Per verificare che l'urto sia elastico bisogna osservare se il centro di massa si muove di moto rettilineo uniforme. Per questa ragione è necessario determinare la velocità mediante la formula:

Lo spazio l può essere misurato con un righello considerando la distanza tra due centri di massa successivi; il tempo, invece, è un valore costante t = 0,1 s perché pari all'inverso della frequenza di registrazione υ = 10 Hz, che è stata selezionata per effettuare l'urto tra i due alianti. 

Quindi il centro di massa del sistema si muove di moto rettilineo uniforme.

II FASE

Nella seconda parte dell'esperienza abbiamo tracciato i vettori spostamento dei due alianti prima dell'urto S₁ e S₂ e i vettori spostamento degli stessi dopo l'urto S^'₁ e S^'₂.

In seguito si sono tracciati i vettori variazione di velocità ∆V₁ e ∆V₂ i cui valori sono stati determinati con l'utilizzo del righello, questo perchè proporzionali ai vettori spostamento avendo utilizzato sempre lo stesso intervallo di tempo, quindi l'errore di sensibilità è ∆V = 0,001 m :

Essendo l'urto elastico, l'impulso totale si conserva: ∆P₁ = ∆P₂; quindi:

Il rapporto tra le velocità è = con un errore assoluto: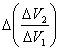 = = 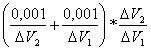0,06

Il rapporto tra le masse è= con un errore assoluto: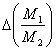= = 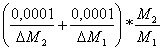0,0003

Il modulo della discrepanza tra il rapporto delle velocità e il rapporto delle masse è:

=

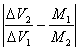L'errore sulla discrepanza è pari alla somma degli errori assoluti dei due rapporti ed è:

=

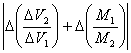Sapendo che l'errore massimo sulla discrepanza deve essere maggiore o uguale del modulo della discrepanza

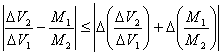
possiamo dire che i risultati ottenuti dimostrano che l'urto descritto dai due alianti è elastico.

III FASE

Nella terza e ultima fase dell'esperienza si è determinata l'energia cinetica prima e dopo l'urto per entrambi gli alianti con lo scopo di verificare la conservazione delle stesse energie.

L'energia cinetica dei due alianti prima e dopo l'urto si determina utilizzando la seguente formula:

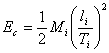
Per la conservazione dell'energia cinetica avremo che:  K₁ = K₂

Se indichiamo con le velocità dei due alianti, dove sono i generici spostamenti dei due alianti prima e dopo l'urto e = 0,3 s l'intervallo di tempo costante in cui gli alianti hanno percorso tali distanze, con ∆M_i e ∆l₁ gli errori assoluti sulle masse e sulle distanze, allora possiamo scrivere la formula che permette di determinare l'errore assoluto su K₁ e K_2.

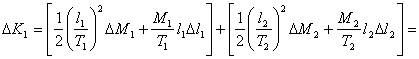
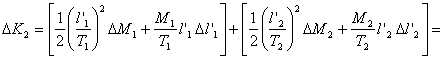
Quindi K₁ = (0,125 ± 0,0026) J e K₂ 0,122 ± 0,0025) J .

Il modulo della discrepanza tra le due variazioni di energia cinetica K₁ e K₂ è

0,003 J

L'errore assoluto sulla discrepanza è:

0,005

Come ci si aspettava i risultati ottenuti dimostrano che l'errore assoluto sulla discrepanza è maggiore della discrepanza stessa.