 |  | |
|
| | |
|
| |
CALCOLO DELLA COSTANTE CHE LEGA IL VOLUME ALLA PRESSIONE DI UN GAS A TEMPERATURA COSTANTE
Lo scopo di questa relazione è calcolare la costante che lega il
volume e la pressione di un gas (aria) a temperatura costante (
.
Si può quindi dedurre che il rapporto fra i due fattori del secondo membro dell'equazione risulta costante e che le due grandezze sono legate da una relazione di proporzionalità inversa.
I materiali usati in quest'attività sono:
un'asta metallica;
due tubi in vetro;
del mercurio;
un tubo in plastica;
un tappo per chiudere uno dei tubi in vetro;
un morsetto da fissare alla sbarra metallica e da far scorrere su di essa.
Mi sono servito anche di due strumenti di misura:
un
termometro con scala in gradi Farenith e Celsius (sX:
un
metro (sX: 1 mm; Xmax:
Per costruire la struttura su cui effettuare le misure è necessario procedere in questo modo: si fissa innanzitutto il morsetto all'asta metallica, si tappa una delle canne in vetro con il tappo apposito e si unisce all'altra per mezzo della conduttura in materiale plastico. Si riempie il condotto formato in questo modo di mercurio, lasciando dell'aria nell'estremità tappata (per un volume di 2,45∙103 mm3), e lo si fissa al morsetto. Si unisce infine il metro alla colonna metallica e si fa in modo che in ambedue i tubi di vetro il livello del mercurio raggiunga lo zero del metro.
Si porta più in alto (in questo caso sempre di 70 mm) l'estremità del condotto non tappata, tenendo invece l'altra ancorata al supporto. Si noterà che il mercurio presente nel tubo tappato aumenterà il suo livello di pochissimo.
Grazie a questo procedimento si è in grado di ricavare i seguenti dati:
|
h1(mm) |
h2(mm) |
|
|
|
|
|
7,00E+01 |
|
1,10E+01 |
1,40E+02 |
|
1,70E+01 |
2,10E+02 |
|
2,20E+01 |
2,80E+02 |
|
2,60E+01 |
3,50E+02 |
|
2,90E+01 |
4,20E+02 |
|
3,30E+01 |
4,90E+02 |
|
3,60E+01 |
5,60E+02 |
|
3,90E+01 |
6,30E+02 |
|
4,10E+01 |
7,00E+02 |
Usando la formula per il calcolo del volume di un cilindro(
), in cui l'altezza del solido è ricavata dalla differenza
tra l'altezza totale del tubo(85 mm) e quella misurata(h1), mentre l'area
di base è stata ottenuta grazie all'equazione(
), a cui è stato sommato il volume della parte di tubo
lasciata libera dal tappo(49,5mm3) e quella per il calcolo della
pressione ricavata dalla Legge di Stevino 
dove d è la densità
del mercurio (13,590 mg/mm3) e h è l'h2 della tabella si
è giunti alla seguente tabella di dati.
|
V(mm3) |
P(Pa) |
|
2,45E+03 |
1,01E+05 |
|
2,28E+03 |
9,32E+09 |
|
2,14E+03 |
1,86E+10 |
|
1,97E+03 |
2,80E+10 |
|
1,83E+03 |
3,73E+10 |
|
1,72E+03 |
4,66E+10 |
|
1,63E+03 |
5,59E+10 |
|
1,52E+03 |
6,53E+10 |
|
1,43E+03 |
7,46E+10 |
|
1,35E+03 |
8,39E+10 |
|
1,29E+03 |
9,32E+10 |
.da cui si ricava il seguente grafico:
|
V(m3) |
P(Pa) |
|
2,45E+12 |
1,01E+05 |
|
2,28E+12 |
9,32E+09 |
|
2,14E+12 |
1,86E+10 |
|
1,97E+12 |
2,80E+10 |
|
1,83E+12 |
3,73E+10 |
|
1,72E+12 |
4,66E+10 |
|
1,63E+12 |
5,59E+10 |
|
1,52E+12 |
6,53E+10 |
|
1,43E+12 |
7,46E+10 |
|
1,35E+12 |
8,39E+10 |
|
1,29E+12 |
9,32E+10 |
Il grafico evidenzia una relazione di proporzionalità inversa fra le
due grandezze in questione perciò ho applicato la formula 
che mi ha consentito di ottenere una tabella di dati con il
relativo grafico:
|
1/V |
P(Pa) |
|
4,08E-13 |
1,01E+05 |
|
4,38E-13 |
9,32E+09 |
|
4,67E-13 |
1,86E+10 |
|
5,07E-13 |
2,80E+10 |
|
5,46E-13 |
3,73E+10 |
|
5,82E-13 |
4,66E+10 |
|
6,12E-13 |
5,59E+10 |
|
6,58E-13 |
6,53E+10 |
|
6,97E-13 |
7,46E+10 |
|
7,41E-13 |
8,39E+10 |
|
7,73E-13 |
9,32E+10 |
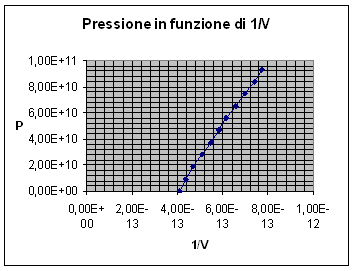
Applicando la formula inversa 
sono stato in grado di calcolare la costante che lega queste
due grandezze ovvero 5,92E-02 Pa∙m3.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
