Laboratorio di Fisica
Studio di una popolazione cellulare
Scopo dell'esercitazione:
Misurare la distribuzione dei diametri e/o
delle aree di alcune cellule.
Materiale usato:
Microscopio ottico con ingrandimenti a 10x, 40x e 100x;
un micrometro montato nell'oculare; un vetrino con cellule di tessuto adiposo. 757h76h
Procedimento:
Accendere la luce del microscopio e
posizionare il vetrino sul traslatore, dopodiché posizionare l'ingrandimento
10x facendo in modo da mettere a fuoco per avere un'immagine nitida delle
cellule. Con tale ingrandimento si riuscirà a vedere un ammasso compatto delle
cellule del tessuto adiposo con varie
colorazioni, a seconda del tipo di cellule presenti. Dopodiché inserire
l'ingrandimento 40x così l'immagine risultaerà solo leggermente sfocata e agendo sulle manopole poste ai lati,
rimettere l'immagine a fuoco. Le cellule saranno distinguibili, ma non sarà
ancora possibile fare la misurazione del diametro cellulare. Infine, inserire
l'ingrandimento 100x e usare le manopole per la messa a fuoco. A questo punto
si può procedere alla misurazione dei diametri e quindi delle aree. Inserire
inoltre, la frequenza dei valori, la media matematica, lo scarto quadratico e
l'errore sulla media.
I diametri misurati sono:
18 ,18
,21 ,17 ,18 ,16 ,19
,18 ,19 ,17
,20 ,18 ,18
,19 ,15 ,19
,20 ,17 ,18
,18.
|
Classi di frequenza
|
Frequenza
|
|
15
|
1
|
|
16
|
1
|
|
17
|
3
|
|
18
|
8
|
|
19
|
4
|
|
20
|
2
|
|
21
|
1
|
La media risulta essere : 18,15.
Calcolare ora lo scarto dal valore medio e poi
elevarlo al quadrato, per ottenere lo scarto quadratico che sarà sempre un
numero positivo. Dopodiché calcolare lo scarto quadratico medio, facendo la
somma di tutti gli scarti quadratici, diviso il numero degli scarti stessi.
|
Scarto
|
|
18 - 18,15 = - 0,15
|
|
18 - 18,15 = - 0,15
|
|
21 - 18,15 = 2.85
|
|
17 - 18,15 = - 1,15
|
|
18 - 18,15 = - 0,15
|
|
16 - 18,15 = - 2,15
|
|
19 - 18,15 = 0,85
|
|
18 - 18,15 = - 0,15
|
|
19 - 18,15 = 0,85
|
|
17 - 18,15 = - 1,15
|
|
20 - 18,15 = 1,85
|
|
18 - 18,15 = - 0,15
|
|
18 - 18,15 = - 0,15
|
|
19 - 18,15 = 0,85
|
|
15 - 18,15 = - 3,15
|
|
19 - 18,15 = 0,85
|
|
20 - 18,15 = 1,85
|
|
17 - 18,15 = -1,15
|
|
18 - 18,15 = - 0,15
|
|
18 - 18,15 = - 0,15
|
|
Scarto^2
|
|
0,0225
|
|
0,0225
|
|
8,1225
|
|
1,3225
|
|
0,0225
|
|
4,6225
|
|
0,7225
|
|
0,0225
|
|
0,7225
|
|
1,3225
|
|
3,4225
|
|
0,0225
|
|
0,0225
|
|
0,7225
|
|
9,9225
|
|
0,7225
|
|
3,4225
|
|
1,3225
|
|
0,0225
|
|
0,0225
|
|
Scarto Quadratico Medio
|
|
[(Σ
scarto ^2) / 20] = 1,8275
|
|
Errore
della media
|
|
18,15
- 18 = 0,15
|
|
18,15
- 18 = 0,15
|
|
18,15
- 21 = -2,85
|
|
18,15 - 17 = 1,15
|
|
18,15
- 18 = 0,15
|
|
18,15
- 16 = 2,15
|
|
18,15 - 19 = -0,85
|
|
18,15 - 18 = 0,15
|
|
18,15 - 19 = -0,85
|
|
18,15 - 17 = 1,15
|
|
18,15 - 20 = -1,85
|
|
18,15 - 18 = 0,15
|
|
18,15
- 18 = 0,15
|
|
18,15 - 19 = -0,85
|
|
18,15 - 15 = 3,15
|
|
18,15 - 19 = -0,85
|
|
18,15 - 20 = -1,85
|
|
18,15 - 17 = 1,15
|
|
18,15 - 18 = 0,15
|
|
18,15
- 18 = 0,15
|
Ora costruire un
istogramma tra classi di frequenza e frequenze stesse:
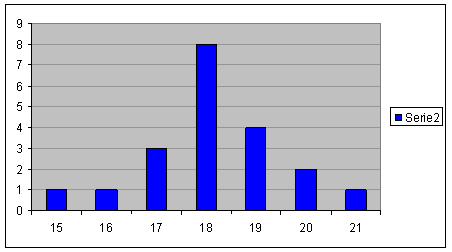
E' possibile fare
quanto sopra anche in base alle aree e non ai soli diametri
|
Aree delle cellule
|
Classi di frequenza
|
Frequenza
|
Media
|
Scarto^2
|
Scarto^2 Medio
|
Errore Sulle Media
|
|
254,34
|
176,625
|
1
|
260,031
|
32,387481
|
1471,722465
|
5,691
|
|
254,34
|
200,96
|
1
|
|
32,387481
|
|
5,691
|
|
346,185
|
226,865
|
3
|
|
7422,5117
|
|
-86,154
|
|
226,865
|
254,34
|
8
|
|
1099,9836
|
|
33,166
|
|
254,34
|
283,385
|
4
|
|
32,387481
|
|
5,691
|
|
200,96
|
314
|
2
|
|
3489,383
|
|
59,071
|
|
283,385
|
346,185
|
1
|
|
545,40932
|
|
-23,354
|
|
254,34
|
|
|
|
32,387481
|
|
5,691
|
|
283,385
|
|
|
|
545,40932
|
|
-23,354
|
|
226,865
|
|
|
|
1099,9836
|
|
33,166
|
|
314
|
|
|
|
2912,653
|
|
-53,969
|
|
254,34
|
|
|
|
32,387481
|
|
5,691
|
|
254,34
|
|
|
|
32,387481
|
|
5,691
|
|
283,385
|
|
|
|
545,40932
|
|
-23,354
|
|
176,625
|
|
|
|
6956,5608
|
|
83,406
|
|
283,385
|
|
|
|
545,40932
|
|
-23,354
|
|
314
|
|
|
|
2912,653
|
|
-53,969
|
|
226,865
|
|
|
|
1099,9836
|
|
33,166
|
|
254,34
|
|
|
|
32,387481
|
|
5,691
|
|
254,34
|
|
|
|
32,38748
|
|
5,691
|
Costruire ora il diagramma basato sulle aree
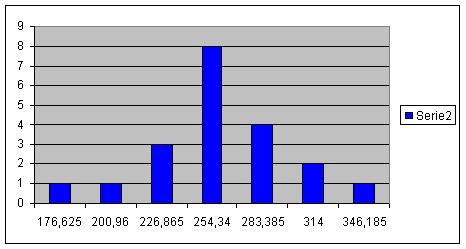
Effettuato ora il
test del c2 sulla
distribuzione facendo l'ipotesi che essa sia gaussiana e verificando che essa
sia accettabile.
|
Intervallo
di aree misurate (mm2)
|
Numero
di cellule osservate (Oi)
|
Intervallo
di z
|
Probabilità
Pk
|
Numero
atteso di cellule= 20xp
|
|
|
|
z = (x-media)/s
|
|
|
|
164;188
|
1
|
-96; -72
|
0.25
|
0,5
|
|
188;212
|
1
|
-72; -48
|
0.95
|
1,9
|
|
212;238
|
3
|
-48; -22
|
1.7
|
3,4
|
|
238;266
|
8
|
-22; 6
|
4.2
|
8,4
|
|
266;295
|
4
|
6; 35
|
1.7
|
3,4
|
|
295;325
|
2
|
35; 65;
|
0.95
|
1,9
|
|
325;350
|
1
|
65; 90
|
0.5
|
0,5
|
Dopodiché calcolare la T di Student usando la seguente
formula:
T=Σ((Oi-Ai)^2)/Ai, il risultato è 1,605.
Poiché abbiamo 7 classi nell'istogramma, il
numero di gradi di libertà è a 7-1=6. Dalle tavole, per 6 gradi di
libertà,
c2 è uguale a 14,02; il nostro valore è minore di
quello critico al 95% (T<c2), per cui l'ipotesi che la distribuzione osservata sia Gaussiana viene
accettata.
|
