|
|
| |
DISPENSA DIDATTICA
A CURA DEL DOTT. MATTEO M. CATI
PER LE ESERCITAZIONI DI MICROECONOMIA - CLEM
A.A.: 2002 - 2003
a) Teoria del Consumatore Pgg.
1. - Funzioni di Utilità
- Curve di Indifferenza
- Saggio Marginale di Sostituzione tra x1 e x2
- Scelta Ottimale del Consumatore ....................
(i) Funzione di Utilita' Cobb - Douglas:..U = x11/3 x21/2
(ii) Perfetta Sostituibilità:......... U = 4x1 + 6x2
(iii) Perfetta Complementarità:.......U = min
(iv) Preferenze quasi lineari:........U = x11/2 + x2
(v) Non Convessita' delle Preferenze: ... U = x13 + 4x23
2. Funzioni di Domanda Marshalliane e Funzioni di Domanda di Engel.....10
b) Scelta tra consumo e tempo libero
3. Il Modello e l'Offerta di lavoro........................13
c) Effetto prezzo, Effetto di Sostituzione ed Effetto Reddito:
4. Metodo della Variazione di Costo (Slutsky)................15
5. Metdodo della Variazione Compensativa del Reddito (Hicks).........16
d) Riferimenti bibliografici
e) Appendice:
Come calcolare le Utilità Marginali ed il Saggio Marginale di Sostituzione per le Funzioni di Utilità (a),(b),(c),(d),(e).......................19
Date le seguenti funzioni di utilità:
(i) Funzione di Utilita' Cobb - Douglas:.. U = x11/3 x21/2
(ii) Perfetta Sostituibilità:......... U = 4x1 + 6x2
(iii)Perfetta Complementarità:....... U = min
(iv) Preferenze quasi lineari:........ U = x11/2 + x2
(v) Non Convessita' delle Preferenze: ... U = x13 + 4x23
Per ognuna di esse, determiniamo:
a) l'espressione della curva di indifferenza
b) il Saggio Marginale di Sostituzione tra x1 ed x2
c) la rappresentazione grafica delle curve di indifferenza
d) la scelta ottimale del consumatore
L'espressione analitica di tale funzione è:
U = U(x1,x2) = x1αx2β (1)
Con α e β parametri - due numeri positivi.
a) Curve di indifferenza: Vediamo ora come determinare l'espressione delle relative curve di indifferenza, che possiamo definire come l'insieme degli x1 ed x2 cui corrisponde la stessa utilità U = k: dato un determinato valore dell'utilità U = k, esplicitiamo x2 ed otteniamo:
x1 x2 = k da cui x2 = k1/ /x1
nell'esempio avremo x2 = k 2/x12/3
b) Saggio Marginale di Sostituzione tra x1 ed x2: calcoliamo ora SMS(x1,x2), che considerermo in valore assoluto, ovvero SMS(x1,x2) , ottenendo:
SMS(x1,x2) = Ux1/Ux2 = αx2/βx1
(con Ux1 ed Ux2 si indicano rispettivamente l'utilità marginale rispetto ad x1 e rispetto ad x2). Nell'esempio avremo SMS(x1,x2) = Ux1/Ux2 = 2x2/3x1.
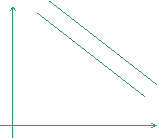
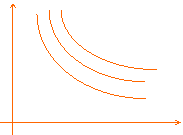
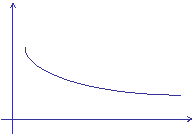
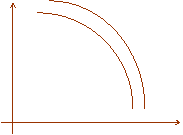
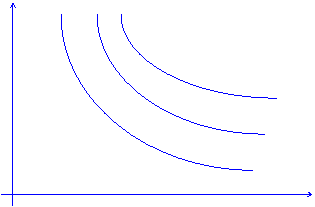
c) rappresentazione grafica delle curve di indifferenza: in questo caso le curve di indifferenza sono regolari - 'well behaved' - e soddisfano determinate proprietà di regolarità (continue, decrescenti nel piano illustrat 939d37j o da sinistra verso destra, e così via) - si veda la figura 1 - (i).
![]()
 x2 x2 x2
x2 x2 x2
![]()

U''' U''' U'''
U'' U'' U''
![]() U' =
k U' = k U' = k
U' =
k U' = k U' = k
![]()
0 x1 0 x1 0 x1
i. ii. iii.
x2 x2
![]()
![]()
![]() U''' U'''
U''' U'''
U''
![]() U'= k U =
k U''
U'= k U =
k U''
0 x1 0 x1
iv. v.
d) Scelta ottimale del consumatore: data la funzione di utilità in (1), se con R indichiamo il reddito e con px1 e px2 rispettivamente il prezzo del bene 1 e del bene 2, la scelta ottimale per il consumatore può essere individuata:
1.a) tramite le seguenti espressioni:
x*1 = [α/(α + )](R/px1) (2)
x*2 = [ )](R/px2)
1.b) tramite la soluzione del seguente sistema a due equazioni e due incognite:
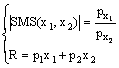
da cui la scelta ottimale x*1 ed x*2. Graficamente l'equilibrio è rappresentato in Figura 2:
x2
x*2 Equilibrio
U
0 x*1 x1
Figura 2: Scelta del Consumatore per le Funzioni
di Utilità Cobb Douglas
Esempio (i): Sia ora U = U(x1,x2) = x11/3 x21/2 la funzione di utilità, R = 400 il reddito, px1 = 1/2 e px2 = 1/4 rispettivamente il prezzo del bene 1 e del bene 2. Vogliamo determinare la scelta ottimale del consumatore.
In questo caso la funzione di utilità è di tipo Cobb - Douglas e, al fine di determinare la scelta ottimale del consumatore, è possibile utilizzare l'espressione (2), ottenendo:
x1* =
x2* =
L'utilità in corrispondenza della soluzione è data da U = U(x1*,x2*) = (320)1/3 (960)1/2 = (6,84)( 30,98)= 211,90.
Possiamo determinare la scelta ottimale del consumatore precedente tramite la soluzione del seguente sistema - si veda il sistema (3):
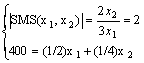
da cui x*1 = 320 e x*2 = 960.
(ii) Perfetta Sostituibilità tra beni
L'espressione della funzione di utilità, in termini generici, per beni legati da una relazione di perfetta sostituibilità è data da:
U = U(x1,x2) = ax1 + bx2
Con a,b due numeri positivi che rappresentano il valore dato dal consumatore ai due beni.
a) Curve di indifferenza: Dato un determinato valore dell'utilità U = k, esplicitiamo x2 ed otteniamo:
x2 = (k - ax1)/b
Nell'esempio (ii) abbiamo la funzione di utilità U = 4x1 + 6x2 e l'espressione della relativa curva di indifferenza è data da : x2 = (k - 4x1)/6.
b) Saggio Marginale di Sostituzione tra x1 ed x2: calcoliamo ora SMS(x1,x2), che considerermo in valore assoluto, ovvero SMS(x1,x2) , ottenendo:
SMS(x1,x2) = Ux1/Ux2 = a/b
Nell'esempio avremo SMS(x1,x2) = Ux1/Ux2 = 4/6 = 2/3.
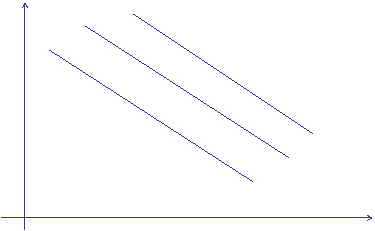
c) rappresentazione grafica delle curve di indifferenza: in questo caso le curve di indifferenza sono lineari - si veda la figura 1 - (ii).
d) Scelta ottimale del consumatore: Sia U(x1,x2) = ax1 + bx2 la funzione di utilità per beni sostituti perfetti; in questo caso, dati R, px1 e px2, la scelta ottimale sarà determinabile:
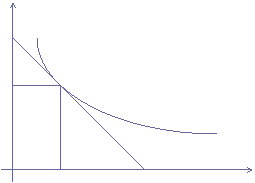
2.a) tramite il confronto fra |SMS(x1 , x2)| ed il prezzo relativo px1/px2 - Figura 3 - in modo tale che:
I) se |SMS(x1 , x2)| > px1/px2 la scelta ottimale è data da x*1=(R/px1) e x*2 = 0 (4)
II) se |SMS(x1 , x2)| < px1/px2 la scelta ottimale è data da x*1 = 0 e x*2=(R/px2)
III)
se |SMS(x1 , x2)| = px1/px2 la scelta ottimale è data da 0 ![]() x*1
x*1 ![]() R/px1 e
R/px1 e
R/px2 ![]() x*2
x*2 ![]()
Le soluzioni I) e II) si dicono d'angolo, mentre la III) rappresenta infinite soluzioni.
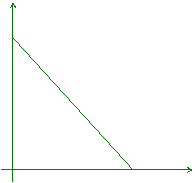
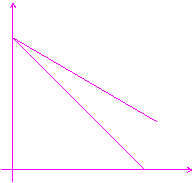
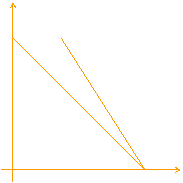
x2 x2 x2
![]() U
U
x*1= 0, x*2 = R/px2
U
![]()
x1 0 x1 0 x1
I) x*1=R/px1 , x*2 = 0 II) III)
Figura 3: Scelta ottimale del Consumatore
per beni Sostituti Perfetti
2.b) tramite il confronto fra il valore che la funzione di utilità assume in corrispondenza delle due possibili soluzioni cosidette d'angolo (x*1 = R/px1 , x*2 = 0) e (x*1 = 0 , x*2 = R/px2), ottenendo come soluzione quella avente utilità più elevata.
Esempio (ii): Data la funzione di utilità U = U(x1,x2) = 4x1 + 6x2, sia R = 240 il reddito, px1 = 3 e px2 = 4. Vogliamo determinare la scelta ottimale del consumatore.
In questo caso la funzione di utilità è lineare ed il bene 1 e 2 sono perfetti sostituti. Per determinare la scelta ottimale è possibile applicare il metodo illustrato prima, (4), che consiste nel confronto tra SMS(x1,x2) = Ux1/Ux2 = 4/6 = 2/3 ed il prezzo relativo px1/px2 = 3/4.
Dato che 2/3 < 3/4, Figura 3 - II), la soluzione si troverà sull'asse delle ordinate e sarà data da: x1* = 0 (ottenuta dal vincolo di bilancio avendo imposto x1 = 0) e x2* = 240/4 = 60; l'utilità corrispondente è data da U = U(x1*,x2*) = 4(0) + 6(60) = 360.
Un metodo alternativo per risolvere questo esercizio è quello di individuare le due possibili soluzioni d'angolo (date da (1) x1* = R/px1 , x2* = 0 e (2) x1* = 0 , x2* = R/px2) e confrontare il valore che la funzione di utilità assume in corrispondenza delle due soluzioni, scegliendo quello più elevato.
Nell'esercizio avremo:
x1* = 240/3 = 80 , x2* = 0
x1* = 0 , x2* = 240/4 = 60
e dato che U'(80,0) = 320 < U''(0,60) = 360 la scelta ottimale del consumatore è data da x1* = 0 , x2* = 60.
La funzione di utilità è del tipo:
U = U(x1,x2) = min
con A1 e A2 numeri positivi. Esempio tipico di beni perfetti complementi è scarpa destra e scarpa sinistra.
a) Curve di indifferenza: Dato un determinato valore dell'utilità U = k, esplicitiamo x2 ed otteniamo:
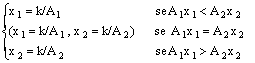
b) Saggio Marginale di Sostituzione tra x1
ed x2: in questo caso avremo SMS(x1,x2) = Ux1/Ux2
= 0 se A1x1 > A2x2 oppure ![]() se A1x1
se A1x1
![]() A2x2
.
A2x2
.
c) rappresentazione grafica delle curve di indifferenza: in questo caso le curve di indifferenza sono lineari - si veda la figura 1 - (iii).
iii) Scelta ottimale del consumatore: Sia U = U(x1,x2) = min[A1x1 , A2x2] la funzione di utilità, per beni perfetti complementi. Dati R, px1 e px2, per determinare la scelta ottimale per il consumatore, dato che non è possibile utilizzare il |SMS(x1 , x2)|, risolviamo il seguente sistema:
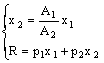
con ![]() l'espressione della semiretta uscente
dall'origine e congiungente tutti i punti d'angolo delle curve di indifferenza
- curva reddito consumo - in Figura 4. Risolvendo il sistema si ottiene la
scelta ottimale x*1 ed x*2.
l'espressione della semiretta uscente
dall'origine e congiungente tutti i punti d'angolo delle curve di indifferenza
- curva reddito consumo - in Figura 4. Risolvendo il sistema si ottiene la
scelta ottimale x*1 ed x*2.
x2 Figura 4: Scelta ottimale del consumatore
per beni complemtari perfetti
![]() x*2 U
x*2 U
0 x*1 x1
Esempio: Sia U = U(x1,x2) = min la funzione di utilità, R = 300, px1 = 1/2 e px2 = 1/3. Determiniamo la scelta ottimale del consumatore, risolvedno il seguente sistema - si veda (5):
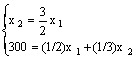
da cui x*1 = 300 e x*2 = 450.
(iv) Preferenze quasi lineari
In questo caso la funzione di utilità è del tipo:
U = U(x1,x2) = n(x1) + x2
Con n(x1) = x11/2 oppure lnx1 ed altri.
a) Curve di indifferenza: Dato un determinato valore dell'utilità U = k, esplicitiamo x2 ed otteniamo:
x2 = (k - n(x1))
Nell'esempio (iv) abbiamo la funzione di utilità x11/2 + x2 = k da cui x2 = k - x11/2.
b) Saggio Marginale di Sostituzione tra x1 ed x2: calcoliamo ora SMS(x1,x2), che considerermo in valore assoluto, ovvero SMS(x1,x2) , ottenendo:
SMS(x1,x2) = Ux1/Ux2 = n'(x1)
dove n'(x1) rappresenta la derivata della funzione n(x1) rispetto ad x1. Nell'esempio avremo SMS(x1,x2) = Ux1/Ux2 = 1/2x11/2.
c) rappresentazione grafica delle curve di indifferenza: in questo caso le curve di indifferenza sono lineari - si veda la figura 1 - (iv).
d) Scelta ottimale del consumatore: 4) Sia U = U(x1,x2) = n(x1) + x2 la funzione di utilità, di tipo semilineare. Il problema di scelta si risolve tramite il sistema (3).
Esempio: Data U = x11/2 + x2 la funzione di utilità, R = 5, px1 = 4 e px2 = 2, determiniamo l'equilibrio tramite il seguente sistema:
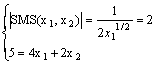
da cui x*1 = 1/16 e x*2 = (5 - ¼)/2 = 2.37.
(v) Non Convessita' delle Preferenze
In questo caso la stuttura delle preferenze non è convessa. Un esempio di questo tipo di funzione di utilità, che rappresenta questa struttura delle preferenze, è U = U(x1,x2) = x13 + 4x23.
a) Curve di indifferenza: Dato un determinato valore dell'utilità U = k, esplicitiamo x2 e, dalla x1 3 + 4x23 = k, otteniamo x2 = [(k - x13)/4]1/3
b) Saggio Marginale di Sostituzione tra x1 ed x2: calcoliamo ora SMS(x1,x2), che considerermo in valore assoluto, ovvero SMS(x1,x2) , ottenendo:
SMS(x1,x2) = Ux1/Ux2 = x13/4x22
Come vedremo in seguito non utilizzeremo il Saggio Marginale di Sostituzione per determinare la scelta ottimale.
c) rappresentazione grafica delle curve di indifferenza: in questo caso le curve di indifferenza sono lineari - si veda la figura 1 - (v).
d) Scelta ottimale del consumatore: Sia U = U(x1,x2) = x1a + x2b, con a e b numeri positivi - preferenze non convesse. In questo caso la soluzione al problema di scelta si determina con il metodo illustrato nel punto 2.b).
Esempio: Sia U = U(x1,x2) = x13 + 4x23 la funzione di utilità; dati R = 200, px1 = 2 e px2 = 4.
La struttura delle preferenze del consumatore è non convessa. Se si risolve il problema di scelta del consumatore tramite il consueto sistema non si ottiene un punto di massimo ma di minimo. La soluzione infatti è d'angolo, Figura 5, e si determina seguendo i seguenti passi:
PRIMO PASSO si calcolano le possibili soluzioni d'angolo e le corrispondenti utilità.
La prima soluzione d'angolo è x1* = 100 e x2* = 0 e l'utilità è data da U' = 1003 = 1000000, mentre la seconda è data da x1* = 0 e x2* = 50 e l'utilità è data da U'' = 4(50)3 = 500000.
SECONDO PASSO La soluzione è data dalla combinazione di beni cui corrisponde la più elevata utilità, ovvero, dato che 1000000 > 500000, x1* = 100 e x2* = 0.
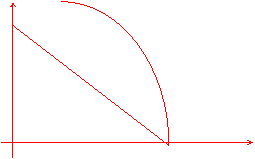
x
U = 1000000
0 x1
Figura 5
2. FunzionE di Domanda Marshalliana e FunzionE di Domanda di
Engel
Dati R = 50, px1 = 1/2 e px2 = 1/2, determinare le funzioni di Domanda Marshalliane per il bene 1 ed il bene 2, le funzioni di Domanda di Engel per il bene 1 ed il bene 2 se:
(i) U(x1,x2) = x11/3 x21/2
La funzione è di tipo Cobb - Douglas e si procede come segue.
Funzione di Domanda Marshalliana
Per determinare la funzione di domanda Marshalliana per il bene 1 si può utilizzare l'espressione (2), ottenendo:
x1 = (50/px1)
da cui x1 = 20/px1 che è la funzione richiesta.
Similmente per determinare la funzione di Domanda Marshalliana per il bene 2, utilizzando l'espressione (2), si ottiene:
x2 = (50/px2)
da cui la funzione x2 = 50/px2 .
Funzione di Domanda di Engel
Per determinare la funzione di domanda di Engel per il bene 1, utilizzando l'espressione (2), si ottiene:
x1 = [R/(1/2)]
da cui x1 = 4R/5.
Similmente per il bene 2.
x2 = [R/(1/2)]
ottenendo così x2 = 6R/5.
(ii) U = U(x1,x2) = 4x1 + 6x2;
Funzione di Domanda Marshalliana
Calcolando SMS(x1,x2) = Ux1/Ux2 = 2/3; così la funzione di domanda Marshalliana per il bene 1 sarà data da:

che può essere riscritto come segue:

Similmente per il bene 2 avremo:
Graficamente, Figura 6, la funzione di domanda Marshalliana per il bene 1 si presenta nel modo seguente:
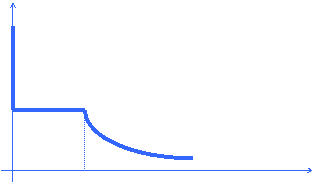 Px1
Px1
1/3
0 150 x1
Figura 6
Per la funzione di domanda di Engel per il bene 1 si ottiene quanto segue:
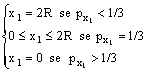
Analogo risultato si ottiene per il bene 2.
(iii) U = U(x1,x2) = min[3x1, 2x2];
Funzione di Domanda Marshalliana
Per determinare la funzione di domanda Marshalliana per il bene 1, si risolve il seguente sistema:
![]()
ottenendo x1 = 50/(px1 + 3/4).
Similmente per la funzione di domanda Marshalliana per il bene 2 si ottiene: x2 = 50/(2/3 + px2).
Funzione di Domanda di Engel
Per individuare la funzione di Domanda di Engel per il bene 1 si risolve il seguente sistema:
![]()
da cui x1 = 4R/5. Per il bene 2 si avrà: x2 = 6R/5.
b) Scelta tra consumo e tempo libero
Consideriamo il seguente esercizio:
Sia U = U(c,TL) = c1/2 + TL la funzione di utilità, con c il bene di consumo e TL il tempo libero. Sia inoltre T^ = 24 l'orizzonte temporale che l'individuo ha a disposizione, w il prezzo del lavoro L e p il prezzo del bene di consumo. Vogliamo determinare la scelta tra consumo e tempo libero e la funzione di offerta di lavoro.
Soluzione:
Per determinare la soluzione al problema di massimizzazione vincolata:
max c , TL U = c1/2 + TL
tale che pc = w(24 - TL)
risolviamo il seguente sistema:
![]()
da cui otteniamo c* = (w/2p)2 e TL* = 24 - (w/4p), che è la scelta ottimale. Per determinare la funzione di offerta di lavoro avremo: Lo = 24 - TL* da cui Lo = w/4p, crescente rispetto al salario reale - Figura 7. Si osservi che il tempo libero è un bene normale:
![]()
 (w/p) Lo
(w/p) Lo
![]()
c) EFFETTO PREZZO - EFFETTO DI SOSTITUZIONE ED EFFETTO REDDITO
Questa Esercitazione si occupa dello svolgimento di alcuni esercizi sulla scomposizione dell'effetto prezzo in effetto di sostituzione ed in effetto reddito:
Esercizio:
Data la funzione di utilità U = x11/2x21/2, il reddito R = 200, il prezzo del bene 1 px1 = 1 ed il prezzo del bene 2 px2 = 1, ipotizzando che il prezzo del bene 1 aumenti a p'x1 = 2, si risponda alle tre precedenti domande.
L'effetto prezzo per il bene 1
Per determinare l'effetto prezzo per il bene 1, misurato dalla variazione della quantità del bene 1 al variare del suo prezzo, è necessario calcolare la scelta ottimale iniziale e la scelta ottimale dopo l'incremento del prezzo del bene 1.
SCELTA OTTIMALE INIZIALE E
Si procede risolvendo il seguente sistema a due incognite, x1 e x2, e due equazioni, la prima delle quali è l'uguaglianza tra il Saggio Marginale di Sostituzione tra il bene 1 ed il bene 2 considerato in valore assoluto ed il prezzo relativo px1/px2 considerato in valore assoluto, mentre la seconda è il vincolo di bilancio:
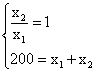
ottenendo x*1 = 100 e x*2 = 100; l'utilità corrispondete è U = (100)1/2(100)1/2 = 100.
NUOVA SCELTA OTTIMALE E'
Si individua ora la scelta ottimale dopo la variazione del prezzo del bene 1, risolvendo il seguente sistema:
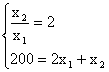
si ottiene x*'1 = 50 ed x*'2 = 100.
L'effetto prezzo Dx1 è calcolato nel modo seguente: Dx1 x*'1 - x*1 ,ovvero
Dx1
5. L'effetto di sostituzione e l'effetto di reddito secondo il metodo della
variazione di costo di Slutsky.
Dopo avere determinato la scelta ottimale iniziale E e la nuova scelta ottimale E', si scompone l'effetto prezzo in effetto di sostituzione ed in effetto reddito secondo il metodo della variazione di costo.
Tramite il metodo della variazione di costo si individuano:
(a) il reddito R' che permette ai nuovi prezzi di acquistare la quantità di bene 1 iniziale, che abbiamo indicato con x1, che è dato da: R' = R + x1(p'x1 - px1), dove R = 200 è il reddito iniziale, x1 = 100 la quantità del bene 1 iniziale, p'x1 e px1 rispettivamente il nuovo prezzo del bene 1 e quello iniziale. Sostituendo si ottiene così R' = 200 + 100(2 - 1) = 300.
(b) la scelta ottimale, che indichiamo nell'esercizio con E'', attuata dal consumatore in corrispondenza del reddito variato R' e dei nuovi prezzi, è individuata risolvendo il sistema con R' = 300 e p'x1/px2 = 2 si ottiene:
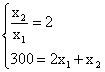
da cui x*''1 = 75 e x*''2 = 150, che è l'ulteriore scelta ottimale E''.
(c) l'effetto di sostituzione e l'effetto di reddito. Si definisce l'effetto di sostituzione come quella parte della variazione della quantità domandata dovuta alla variazione nel saggio di scambio tra i due beni; e l'effetto reddito come quella parte della variazione della quantità dovuta alla variazione del reddito reale. La somma tra effetto di sostituzione ed effetto reddito è pari all'effetto prezzo.
(d) Dato E'', che è l'estremo dell'intervallo, possiamo calcolare, Figura 1:
L'EFFETTO DI SOSTITUZIONE PER IL BENE 1:
E' il passaggio da E ad E'', dato da x''1 - x1: 75 - 100 = - 25
L'EFFETTO REDDITO PER IL BENE 1:
E' il passaggio da E'' a E', dato da x'1 - x''1: 50 - 75 = - 25
Infine si può osservare che la somma dei due effetti è uguale all'effetto
prezzo: - 25 - 25 = - 50
![]()
X2

E''

E' E
![]()
0 X1
Figura 8: Metodo della variazione di costo di Slutsky
6. L'effetto di sostituzione e l'effetto di reddito secondo il
metodo della variazione compensativa del reddito di hicks
Si assuma ora che, dopo aver calcolato E, E' e l'effetto prezzo si scomponga l'effetto prezzo in effetto di sostituzione ed in effetto reddito tramite il metodo della variazione compensativa del reddito di Hicks.
Il metodo della variazione compensativa del reddito individua quella variazione del reddito che compensa il consumatore dell'avvenuta variazione dei prezzi facendo in modo che ottenga la stessa utilità dell'equilibrio iniziale.
La scomposizione dell'effetto prezzo si attua come segue:
Si calcola l'estremo E'' , Figura 2, risolvendo il seguente sistema:
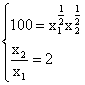
da cui si ottiene x''1 = 100/(2)1/2 e x''2 = 200/(2)1/2.
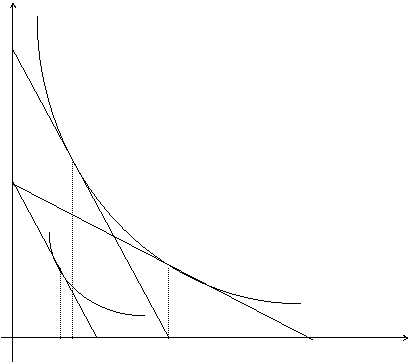
x2
E''
E' E
![]()
U = 100
0 x1
Figura 9: Metodo della Variazione Compensativa
L' EFFETTO DI SOSTITUZIONE PER IL BENE 1:
E' il passaggio da E ad E'', dato da: x1'' - x1 = [100/(2)1/2] - 100 = 71.4 - 100 = -28.6
L'EFFETTO REDDITO PER IL BENE 1:
E' il passaggio da E'' ad E', dato da: x1' - x1'' = 50 - [100/(2)1/2] = 50 - 71.4 = -21.4
La somma dei due effetti è uguale all'effetto prezzo: - 28.6 - 21.4 = - 50
Si è così determinata la scomposizione in base ai due metodi.
Infine osserviamo che possiamo asserire che lo studio dell'effetto di reddito e di sostituzione ci permette di dire se i due bei sono sostituti netti o lordi e complementari netti o lordi.
A tal fine si calcoli l'effetto di sostituzione per il bene 2, ottenendo: 200/(2)1/2 - 100 = 41.42. Al netto dell'effetto reddito al crescere del prezzo del bene 1, x1 diminuisca ed x2 aumenta: i due beni sono sostituti netti.
d) RIFERIMENTI BIBLIOGRAFICI:
Prof.ssa Chirco Alessandra - Microeconomia: Metodi e
Strumenti - 2002 - Esculapio
FRANK: MICROECONOMIA - Mac Graw - Hill - ultima edizione
DELBONO - ZAMAGNI - MICROECONOMIA - Il Mulino - ultima edizione
e) Appendice:
Come calcolare le Utilità Marginali ed il Saggio Marginale di Sostituzione per le Funzioni di Utilità (a),(b),(c),(d),(e)
(a) U = U(Q1,Q2) = Q11/2 Q21/2 FUNZIONE DI UTILITA' COBB - DOUGLAS
SIA LA FUNZIONE AD UNA VARIABILE Y = CXm con C costante ed m l'esponente
LA DERIVATA DELLA PRECEDENTE FUNZIONE E' Cmx(m - 1)
VEDIAMO COME CALCOLARE LE UTILITA' MARGINALI RISPETTO A Q1 E A Q2 UTILIZZANDO QUANTO RIPORTATO NEL RIQUADRO:
PASSO I: PER CALCOLARE LA DERIVATA PARZIALE PRIMA DELLA FUNZIONE DI UTILITA' RISPETTO A Q1 - L'UTILITA' MARGINALE RISPETTO A Q1 - DOBBIAMO IPOTIZZARE Q2 COSTANTE.
PASSO II: IPOTIZZIAMO ORA DI SCRIVERE LA FUNZIONE DI UTILITA' U(Q1 ,Q2) = Q11/2 Q21/2 COME U(Q1,Q2) = CQ11/2 CON C = Q21/2 COSTANTE.
PASSO III: POSSIAMO ORA DERIVARE LA FUNZIONE U(Q1,Q2) = CQ11/2 CONSIDERANDO LA DERIVATA NEL RIQUADRO; AVREMO COSI':
UQ1 = C(1/2)Q1 - 1/2
SOSTITUIAMO ORA A C, Q21/2 ED OTTENIAMO UQ1 Q1 - 1/2 Q21/2 CHE E' QUANTO CERCAVAMO.
PASSO I: PER CALCOLARE LA DERIVATA PARZIALE PRIMA DELLA FUNZIONE DI UTILITA' RISPETTO A Q2 - L'UTILITA' MARGINALE RISPETTO A Q2 - DOBBIAMO IPOTIZZARE Q1 COSTANTE.
PASSO II: IPOTIZZIAMO DI SCRIVERE LA FUNZIONE DI UTILITA' U(Q1 ,Q2) = Q11/2 Q21/2 COME U(Q1,Q2) = CQ21/2 CON C = Q11/2 COSTANTE.
PASSO III: POSSIAMO ORA DERIVARE LA FUNZIONE U(Q1,Q2) = CQ21/2 CONSIDERANDO LA DERIVATA NEL RIQUADRO; AVREMO COSI':
UQ2 = C(1/2)Q2 - 1/2
SOSTITUIAMO ORA A C, Q11/2 ED OTTENIAMO UQ1 Q2 - 1/2 Q11/2.
SAGGIO MARGINALE DI SOSTITUZIONE TRA Q1 E Q2:
CALCOLIAMO IL SAGGIO MARGINALE DI SOSTITUZIONE:
|SMS(Q1 , Q2)| = ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()
POSSIAMO ORA RAPPRESENTARE GRAFICAMENTE LE CURVE DI INDIFFERENZA, OTTENENDO:
 Q2
Q2
U'''
U''
U'
0 Q1
FIGURA 1: CURVE DI INDIFFERENZA
(b) COSIDERIAMO ORA LA FUNZIONE DI UTILITA'
U = U(Q1,Q2) = 3Q1 + 2Q2 FUNZIONE DI UTILITA' LINEARE
SIA LA FUNZIONE AD UNA VARIABILE Y = D + CXm con C , D costanti ed m l'esponente
LA DERIVATA DELLA PRECEDENTE FUNZIONE E' 0 + Cmx(m - 1) = Cmx(m - 1)
VEDIAMO COME CALCOLARE LE UTILITA' MARGINALI RISPETTO A Q1 E A Q2 UTILIZZANDO QUANTO RIPORTATO NEL RIQUADRO:
PASSO I: PER CALCOLARE LA DERIVATA PARZIALE PRIMA DELLA FUNZIONE DI UTILITA' RISPETTO A Q1 - L'UTILITA' MARGINALE RISPETTO A Q1 - DOBBIAMO IPOTIZZARE Q2 COSTANTE.
PASSO II: IPOTIZZIAMO ORA DI SCRIVERE LA FUNZIONE DI UTILITA' U(Q1 ,Q2) = 3Q1 + 2Q2 COME U(Q1,Q2) = D + 2Q1 CON D = 3Q2 COSTANTE.
PASSO III: POSSIAMO ORA DERIVARE LA FUNZIONE U(Q1,Q2) = D + 3Q1 CONSIDERANDO LA DERIVATA NEL RIQUADRO; AVREMO COSI':
UQ1
PASSO I: PER CALCOLARE LA DERIVATA PARZIALE PRIMA DELLA FUNZIONE DI UTILITA' RISPETTO A Q2 - L'UTILITA' MARGINALE RISPETTO A Q2 - DOBBIAMO IPOTIZZARE Q1 COSTANTE.
PASSO II: IPOTIZZIAMO DI SCRIVERE LA FUNZIONE DI UTILITA' U(Q1 ,Q2) = 3Q1 + 2Q2 COME U(Q1,Q2) = D + Q2 CON C = 3Q1 COSTANTE.
PASSO III: POSSIAMO ORA DERIVARE LA FUNZIONE U(Q1,Q2) = D + 2Q2 CONSIDERANDO LA DERIVATA NEL RIQUADRO; AVREMO COSI':
UQ2
POSSIAMO ORA CALCOLARE IL SAGGIO MARGINALE DI SOSTITUZIONE:
|SMS(Q1 , Q2)| = ![]() = 3/2
= 3/2
POSSIAMO ORA RAPPRESENTARE GRAFICAMENTE LE CURVE DI INDIFFERENZA, OTTENENDO:
 Q2
Q2
U'''
U''
U'
0 Q1
FIGURA 2 : CURVE DI INDIFFERENZA LINEARI
(c) CONSIDERIAMO ORA LA FUNZIONE DI UTILITA' U = MIN
IN QUESTO CASO
L'UTILITA' MARGINALE RISPETTO A Q1 E' A1 SE A1Q1
![]() A2Q2 , 0 SE A1Q1 > A2Q2
.
A2Q2 , 0 SE A1Q1 > A2Q2
.
IL SAGGIO MARGINALE
DI SOTITUZIONE TRA Q1 E Q2 E' ![]() SE A1Q1
SE A1Q1
![]() A2Q2 OPPURE 0 SE A1Q1 > A2Q2
.
A2Q2 OPPURE 0 SE A1Q1 > A2Q2
.
LE CURVE DI INDIFFERENZA SONO RAPPRESENTATE GRAFICAMENTE COME SEGUE:
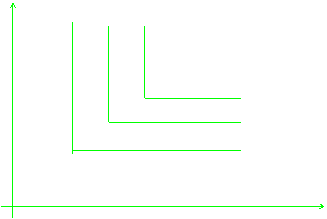 Q1
Q1
U'''
U''
U'
0 Q2
FIGURA 3: CURVE DI INDIFFERENZA AD ANGOLO
Per calcolare le utilità marginali per le funzioni di utilità (e) U = x11/2 + x2 ed (f) U = x12 + 4x22 si usa la regola somma.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025