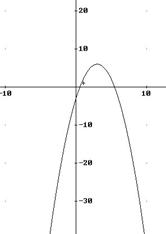
Disegnare, con un software algebrico, la parabola di equazione y = 2x² + 7x - 15 e verificare i risultati ottenuti al punto 1.

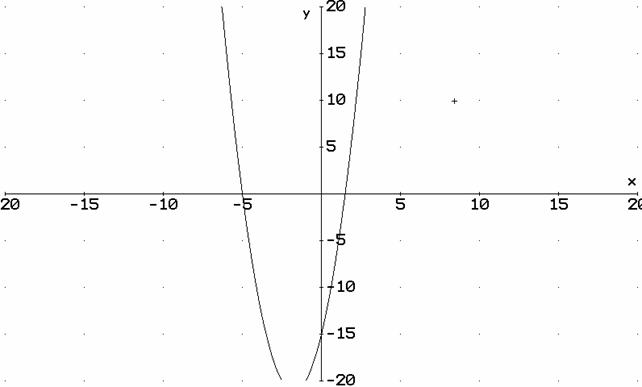
I punti d'incontro con l'asse x sono esattamente a  -5 e a 1,5 che vale a dire 3/2. Abbiamo così verificato l'equazione del punto 1

Ricavare una formula generale per la risoluzione dell' equazione di 2° grado:

ax² + bx + c = 0

dove a,b,c sono numeri reali e a ≠ 0.

Risoluzione dell'equazione:

Utilizzando la formula ricavata al punto 3 risolvere le seguenti equazioni e verificare i risultati, controllandoli anche graficamente.

a) 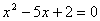  b) c) d)

e)    f) g)

h)    i) l)

USANDO LA FORMULA: GRAFICAMENTE:

a) 

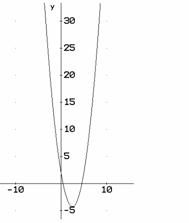
b)  

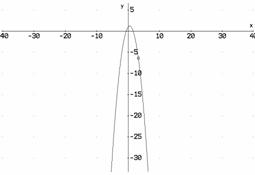
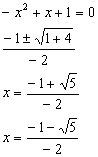
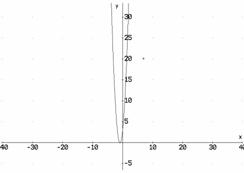
c)

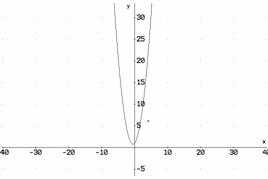
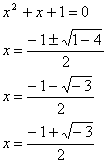
d)

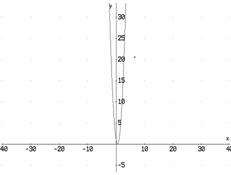
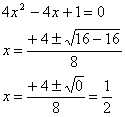
e)

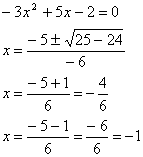
f)

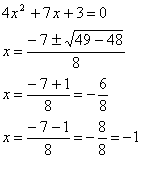
g)

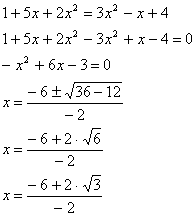
h)

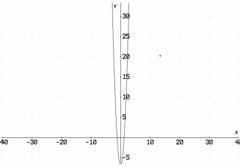
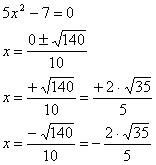
i)

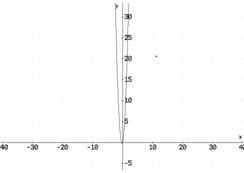
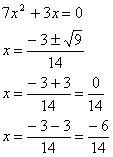
l)

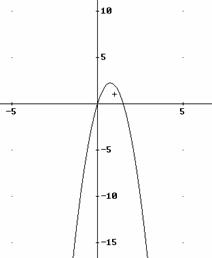
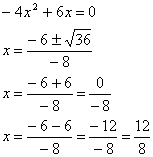
Costruire quattro equazioni di 2° grado, diverse dalle precedenti, soddisfacenti ciascuna a uno dei seguenti requisiti:

a) ammette due soluzioni positive

b) ammette due soluzioni negative

c) ammette due soluzioni di segno contrario

d) non ammette soluzioni

Abbiamo risolto il problema con il metodo della fattorizzazione

a)  

In questo caso x = a due numeri positivi per soddisfare le parentesi

b)

In questo caso x = a due numeri negativi per soddisfare le parentesi

c)

In questo caso invece x = ad un numero positivo (+4) ed ad uno negativo(-2)

d)

Un' equazione di questo tipo non ha risultati poiché un numero qualsiasi al

quadrato addizionato a "+8" non è uguale a 0

Quanto deve essere la larghezza x di un rettangolo di lunghezza 1 per poter ritagliare un quadrato in modo che il rettangolo rimanente risulti simile al rettangolo dato?

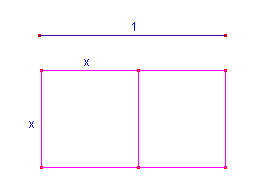
Per arrivare al risultato abbiamo impostato una proporzione mettendo in relazione i lati più lunghi con quelli più corti, dunque:

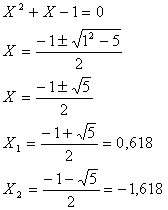
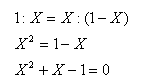
NOTA: Non potrà mai essere (1 - x) : x =1 : x  perché ci sarebbe x al denominatore ma diversi numeratori dunque l'uguaglianza non sarebbe più valida.

(forse si può capire meglio scrivendo la proporzione nel seguente modo:)

Prendiamo ovviamente in considerazione solo il risultato positivo ossia 0,618 che viene chiamato numero d'oro.

L'equazione 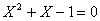ottenuta al punto 6 origina il numero d'oro ( circa 0,618). Considerando che la precedente si può scrivere sotto la forma ovvero , verificare il risultato graficamente con un software algebrico, disegnando le curve e

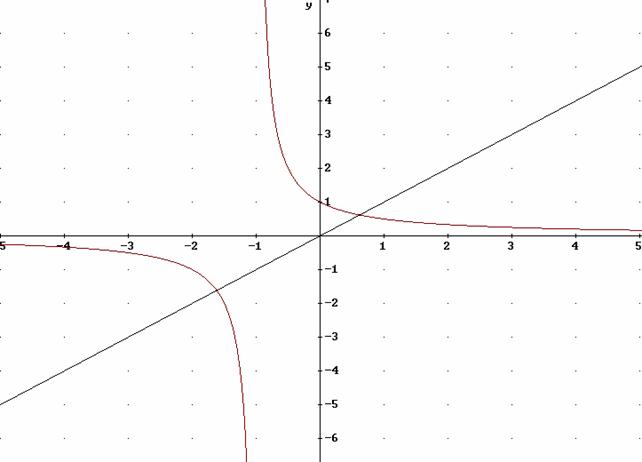
Per risolvere l'equazione anche utilizzando il metodo grafico è necessario che y sia uguale a x.

Per quanto riguarda la soluzione positiva la possiamo trovare nel primo quadrante nel punto di incontro tra la curva e la retta y=x, mentre per la soluzione negativa bisogna prendere in considerazione il terzo quadrante.

Un'altra soluzione per ricavare i punti di incontro è risolvere il sistema:

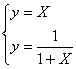
Però c'è un'altra possibilità per arrivare al risultato:

si può infatti disegnare il grafico della funzione y=x²+x-1 riportato in basso:

La parabola taglia l'asse x nel primo quadrante precisamente nel punto 0,618 mentre nel secondo nel punto .

Ritrova il numero d'oro risolvendo l'equazione x²+x-1 con il foglio elettronico

Ecco un'altra strada per arrivare al risultato 0,618: utilizzare il foglio elettronico.

La colonna A corrisponde alle x mentre la colonna B alle y. Iniziamo a inserire 0 nella casella A1 e nella casella A2 inseriamo A1+0,1 per avere un intervallo di ottenendo ciò:

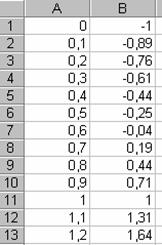
Ora nella casella B1 inserisco l'equazione A1^2+A1-1 in modo da ottenere i valori delle y.

Ciò che determina il risultato dell'equazione è l'intersezione della parabola con l'asse x dove y deve per forza valere , dunque osserviamo la tabella ottenuta e prendiamo in considerazione i valori di y in cui sia compreso (che sono dunque il risultato dell'equazione sarà un numero compreso tra e (vedi figura)

Perciò conviene ridurre l'intervallo (che prima era 0,1) per avere un risultato sempre più preciso. Nella casella C1 scriveremo dunque e nella casella C2 inseriremo C1+ 0,001. La colonna C corrisponderà alle x mentre la colonna D alle y. Proprio nella colonna D scriveremo nuovamente l'equazione C1^2+C1-1 ottenendo questi risultati:

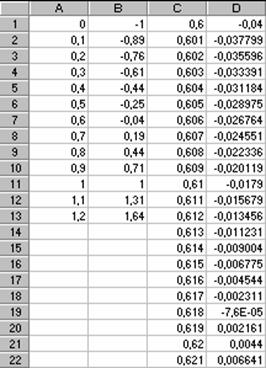
Ora notiamo che il risultato dell'equazione sarà un numero compreso tra 0,618 e .

Si può ancora andare avanti utilizzando intervalli sempre più piccoli ma non si otterrà mai un risultato preciso.

Spiegare come si può risolvere l'equazione x²+x-1=0 utilizzando il tasto (o x^-1) della calcolatrice.

Per semplificare il problema abbiamo trasformato x²+x-1=0 in

Iniziamo a digitare un numero a caso (es. 2) e premiamo il tasto x^-1: questa funzione lo sostituirà alla x e calcolerà il risultato (es.).

Aggiungendo poi 1 (dell'equazione) e premendo nuovamente il tasto x^-1 si otterrà approssimativamente il numero d'oro.

(es.2 1.5 (digitando x^-1) )

Continuando ad aggiungere 1 al risultato precedente e continuando a premere il tasto x^-1 ci avvicineremo in modo sempre più preciso al numero d'oro