|
|
| |
TECNOLOGIA
Studiando il comportamento dell'impresa, dobbiamo esaminare, in primo luogo, i vincoli ai quali è sottoposta.
Infatti, quando un'impresa compie delle scelte, essa tiene conto di molti vincoli: questi possono essere imposti dai clienti, o dai concorrenti, oppure possono essere vincoli naturali.
I vincoli naturali si presentano all'impresa come vincoli tecnologici: solo alcune combinazioni di input consentono di produrre una data quantità di output, quindi, l'impresa deve limitarsi a prendere in considerazione piani di produzione tecnicamente realizzabili.
L'insieme di tutte le combinazioni di input e output tecnicamente realizzabili è detto insieme di produzione.
Supponiamo, per esempio, di avere un solo input, che indichiamo con x, e un solo output, y. L'insieme di produzione può, in questo caso, avere la forma rappresentata in figura:
![]()
Massimo livello di output che può essere prodotto
impiegando un dato livello di input.
y
(OUTPUT
![]() y = (x)
y = (x)
Scelte tecniche possibili

![]()
![]()
![]()
x
(INPUT
Dire che un punto (x; y) si trova all'interno dell'insieme di produzione significa affermare che è tecnicamente possibile produrre una quantità y di output impiegando una quantità x di input.
L'insieme di produzione rappresenta le scelte tecniche possibili per l'impresa.
Finché gli input dell'impresa hanno un costo, ha senso prendere in considerazione soltanto il massimo livello di output che può essere prodotto impiegando un dato livello di input. Questo coinciderà con la frontiera dell'insieme di produzione rappresentato.
La funzione y = (x) corrispondente alla frontiera di questo insieme di produzione è nota come funzione di produzione e misura il massimo livello di input che può ottenersi impiegando una dato livello di input.
La nozione di funzione di produzione può essere estesa anche al caso in cui vi siano più input. Se, per esempio, consideriamo il caso di due input, la funzione di produzione y = (x1, x2) determina la quantità massima di output y che può essere prodotta impiegando x1 unità del fattore 1 e x2 unità del fattore 2.
Quindi, in generale, se indichiamo con y la quantità prodotta di un bene (output) e con x1, x2, .. , xn le quantità impiegate dei fattori produttivi (input), possiamo scrivere:
y = ( x1, x2, .. , xn)
.
Essa è una funzione di produzione microeconomica, dato che si riferisce ad una singola impresa.
FATTORI FISSI E FATTORI VARIABILI
In un dato periodo di tempo, può risultare difficile far variare la quantità impiegata di certi input. Tipicamente un'impresa è obbligata contrattualmente ad utilizzare determinati input a livelli prefissati. Per esempio, l'impresa potrebbe affittare un edificio, con l'obbligo legale di acquistarne la proprietà in un certo periodo di tempo (leasing).
Definiamo fattore fisso quel fattore produttivo che l'impresa deve impiegare in quantità predeterminate.
Se un fattore può essere, invece, impiegato in quantità variabili, lo si definisce fattore variabile.
Nell'analisi del fenomeno della produzione è importante distinguere il breve periodo dal lungo periodo, distinzione su cui si è soffermato in modo particolare l'economista inglese A. Marshall.
Definiamo, quindi, breve periodo quel periodo di tempo in cui alcuni fattori sono fissi, e cioè possono essere utilizzati solo in quantità prefissate.
Nel lungo periodo, invece, l'impresa è libera di variare la combinazione dei fattori produttivi: cioè tutti i fattori sono variabili.
Non vi è una rigida distinzione fra lungo e breve periodo: ciò che conta è che alcuni fattori produttivi sono fissi nel 323e49d breve periodo e variabili nel lungo.
Poiché tutti i fattori sono variabili nel lungo periodo, l'impresa è sempre libera di decidere di utilizzare quantità nulle di input per produrre una quantità nulla di output, cioè può decidere di cessare ogni attività. Quindi il profitto minimo che un'impresa può realizzare nel lungo periodo è un profitto nullo.
Nel breve periodo, l'impresa deve impiegare un certo numero di fattori, anche se ha deciso che la sua produzione sarà nulla. È quindi perfettamente possibile che il profitto dell'impresa sia negativo nel breve periodo. Infatti, se l'impresa prende in affitto un edificio dovrà pagare l'affitto alle scadenze previste, che decida o no di produrre qualche cosa.
Esiste, comunque, anche un'altra categoria di fattori che l'impresa dovrà pagare solo nel caso in cui decida di produrre una quantità positiva di output: per esempio, l'elettricità per l'illuminazione. Se l'output dell'impresa è nullo, non sarà necessario acquistare energia elettrica, ma, se l'impresa produce una quantità positiva di output, dovrà acquistare una quantità fissa di elettricità. Questi fattori, detti fattori quasi-fissi, sono fattori che bisogna utilizzare in quantità fisse, finché la quantità di output è positiva.
PRODUTTIVITÀ MARGINALE E PRODUTTIVITÀ MEDIA
il prodotto totale Il prodotto totale è l'output ottenuto dall'impiego di tutti i fattori produttivi.
Esso è crescente fino ad un certo punto (nel grafico rappresentato da x1C) in cui l'applicazione di una quantità sempre maggiore di un fattore, a quantità date degli altri fattori, non provoca ulteriori aumenti dell'output, anzi addirittura può provocarne una diminuzione.
Graficamente, abbiamo:
![]()
y
![]()
![]()
![]()
![]()
![]()
x1A x1B x1C x1D x1
la produttività marginale Definiamo ora la produttività marginale di un fattore, cioè l'incremento che l'output subisce quando si impiega una unità in più del fattore considerato, ferme restando le quantità impiegate degli altri fattori, cioè:
Dy/Dx1 = (x1+Dx1, x2) (x1, x2) Dx1
.
differenze con l'utilità marginale Il concetto di prodotto marginale è del tutto simile al concetto di utilità marginale nella teoria del consumatore, fatta eccezione per la natura ordinale dell'utilità. Qui stiamo trattando il prodotto fisico: il prodotto marginale di un fattore è un numero preciso che, in linea di principio, può essere misurato.
considerazioni sulla pmg Prendiamo il grafico precedente:
![]()
y
![]()

![]() B C D r
B C D r
![]()
![]()
A
![]()
![]()
![]()
x1A x1B x1C x1D x1
e osserviamo che la produttività marginale non è altro che il coefficiente angolare della retta r passante per il punto A e il punto D, ovvero la tangente dell'angolo a che si forma quando la retta r interseca l'asse delle ascisse.
PMG = Dy / Dx1 = tg a
Se prendiamo l'intervallo Dx1 sempre più piccolo, la retta r ruota intorno al punto A fino a diventare tangente alla curva proprio in quel punto per Dx1 infinitesimo, ovvero per Dx1 . Graficamente, abbiamo:
![]()
 y
y
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
x1A x1B x1C x1D x1
Si ha quindi per Dx1 che la produttività marginale è uguale alla derivata prima della funzione del prodotto totale calcolata in quel punto.
Possiamo scrivere:
lim PMG = lim Dy/Dx1 = y / x1 Dx1 Dx1
.
Dal grafico precedente vediamo che le rette tangenti ai vari punti hanno dapprima un'inclinazione positiva, che man mano diminuisce (rimanendo sempre positiva) fino ad un punto (x1C) in cui è nulla (infatti, la retta diventa parallela all'asse delle ascisse), per diventare poi negativa. Quindi, il grafico relativo alla PMG sarà:
![]()
 PMG
PMG
![]()
x1c x1
Vediamo che la produttività marginale è decrescente.
Supponiamo di disporre di una data quantità del fattore 1 e del fattore 2 e di voler impiegare una quantità addizionale del fattore 1, mantenendo ad un livello prefissato il fattore 2. Chiediamoci come varierà il prodotto marginale del fattore 1.
Se la tecnologia è monotona, l'output totale aumenterà all'aumentare del livello del fattore 1. Ma ci si può attendere che tale aumento avvenga ad un saggio decrescente.
Consideriamo un esempio specifico: una fattoria. Un individuo che lavori su un acro di terra può produrre 30 Kg di frumento. Se impieghiamo due lavoratori sullo stesso appezzamento, mantenendo invariata l'estensione del terreno, otterremo 60 kg di frumento, e quindi, in questo caso, il prodotto marginale di un lavoratore addizionale è 30. Se impieghiamo altri lavoratori la produzione aumenta, ma la quantità addizionale di frumento prodotta dall'ultimo lavoratore impiegato sarà inferiore a 30 Kg. Se si impiegano quattro o cinque lavoratori in più, la quantità addizionale che ciascun lavoratore produce scenderà a 25, 20, 10 kg o anche meno. Se, ammassati su questo acro di terra, ci fossero centinaia di lavoratori, un lavoratore in più potrebbe far diminuire l'output.
Ci possiamo aspettare, dunque, che il prodotto marginale di un fattore diminuisce quando se ne impiegano quantità via via crescenti. Questa viene definita legge della produttività marginale decrescente. Non si tratta di una vera e propria «legge», ma soltanto di una caratteristica comune alla maggior parte dei processi produttivi.
È importante sottolineare che la legge della produttività marginale decrescente è valida solo quando tutti gli altri input siano mantenuti fissi.
la produttività media Definiamo, ora, la produttività media di un fattore come il rapporto fra il prodotto totale e la quantità impiegata del fattore:
Pme =
y/x1
Anche la produttività media di un fattore x1 decresce man mano che cresce la quantità impiegata di x1.
RENDIMENTI DI SCALA
Consideriamo il caso in cui, invece di aumentare l'impiego di uno degli input, mantenendo l'altro fisso, aumentiamo la quantità impiegata di tutti gli input della funzione di produzione. In altri termini, moltiplichiamo la quantità di tutti gli input per una qualche costante.
Se, per esempio, raddoppiamo la quantità impiegata sia del fattore 1 che del fattore 2, possiamo chiederci quanto output sarà prodotto. Possiamo attenderci ragionevolmente che l'output raddoppi. È questo un caso di rendimenti di scala costanti. Nei termini della funzione di produzione, questo significa che raddoppiando la quantità di ciascun input, si produce una quantità doppia di output. Il caso di due input può essere espresso analiticamente nel modo seguente:
(x1; x2) = (2x1; 2x2).
In generale, se si moltiplica per t la quantità impiegata di tutti gli input, nel caso di rendimenti di scala costanti risulterà moltiplicata per t anche la quantità prodotta:
t (x1; x2) = (tx1; tx2)
.
Questo risultato è plausibile perché, normalmente, l'impresa è in grado di replicare esattamente ciò che faceva prima. Se l'impresa dispone di una quantità doppia di ciascun input può, per esempio, costruire due impianti uguali, l'uno accanto all'altro, che produrranno una quantità doppia di output. Se la quantità degli input fosse tripla, costruirebbe tre impianti e così via.
Si noti che è perfettamente possibile che una tecnologia presenti, allo stesso tempo, rendimenti costanti di scala e PMG dei fattori decrescente. I rendimenti di scala descrivono ciò che accade quando si aumentano tutti gli input, mentre la PMG decrescente rappresenta ciò che accade quando si aumenta un solo input e si mantengono gli altri fissi.
Il caso dei rendimenti di scala costanti è quello più «naturale», ma vi sono anche altre possibilità.
Per esempio, può accadere che, moltiplicando per t la quantità impiegata di entrambi gli input, la quantità di output risulti pari a più di t volte la quantità iniziale. È questo il caso di rendimenti di scala crescenti. Formalmente, i rendimenti di scala crescenti sono rappresentati in questo modo:
t (x1; x2) < (tx1; tx2)
per t > 1.
Un oleodotto può rappresentare un esempio significativo di una tecnologia che presenta rendimenti di scala crescenti. Se si raddoppia il diametro della tubatura, si utilizzerà una quantità doppia di materiali, ma la sezione del condotto aumenterà di quattro volte. Quindi, l'oleodotto sarà in grado di trasportare una quantità più che doppia di petrolio.
Ovviamente, c'è un limite. Se si continua a raddoppiare il diametro della tubatura, questa alla fine cederà sotto il suo stesso peso. I rendimenti di scala crescenti sussistono solo per certi livelli di output.
L'altro caso da considerare è quello di rendimenti di scala decrescenti, dove:
t (x1; x2) > (tx1; tx2)
per t > 1.
Questo è un caso un po' particolare. Se otteniamo una quantità meno che doppia di output raddoppiando la quantità impiegata di tutti gli input, qualche cosa non funziona. Dopo tutto, si tratta di replicare esattamente ciò che si faceva prima!
Normalmente, si hanno rendimenti di scala decrescenti quando non si tiene conto di qualche input. Se si raddoppiano tutti gli input tranne uno, non sarà possibile replicare esattamente ciò che si faceva prima, e quindi non si potrà ottenere un output doppio. I rendimenti di scala decrescenti sono in realtà un fenomeno di breve periodo, quando cioè alcuni fattori sono fissi.
Naturalmente, una tecnologia può presentare rendimenti di scala diversi in corrispondenza di livelli diversi di produzione. Può accadere che a livelli di produzione bassi corrispondano rendimenti di scala crescenti - moltiplicando successivamente la quantità impiegata di tutti gli input per una piccola quantità t, la quantità prodotta può aumentare in misura più che proporzionale a t. Successivamente, in corrispondenza di livelli di output più elevati, è possibile che se moltiplichiamo gli input per t anche l'output risulti moltiplicato esattamente per lo stesso fattore.
GLI ISOQUANTI
Supponiamo di dover produrre una data quantità di output impiegando due fattori produttivi. L'insieme di tutte le possibili combinazioni di input 1 e 2 esattamente sufficienti a produrre una data quantità di output è detto isoquanto.
![]() x1
x1

![]() x2
x2
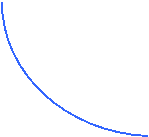
Naturalmente non vi sarà un solo isoquanto, ma ve ne saranno tanti, ciascuno corrispondente ad un livello dato di output. Quindi, tutti i punti situati su di un isoquanto rappresentano lo stesso livello di output, ma ogni isoquanto rappresenta un livello di output più alto man mano che le curve sono situate più a destra (cioè più in alto).
![]()
 x1
x1
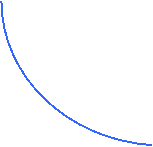
300
200
100
![]() x2
x2
differenza fra isoquanti e curve di indifferenza Gli isoquanti sono simili alle curve di indifferenza, che rappresentano i diversi panieri di consumo che consentono di ottenere un certo livello di utilità. La differenza essenziale fra isoquanti e curve di indifferenza consiste nel fatto che gli isoquanti sono contrassegnati in base alla quantità di output prodotto, e non in base al livello di utilità. Questo significa che i livelli di produzione corrispondenti agli isoquanti sono assegnati dalla tecnologia, e non risentono dell'arbitrarietà che invece caratterizza l'assegnazione dell'utilità alle curve di indifferenza.
esempi di tecnologia
Supponiamo di produrre buche, e che il solo modo di produrle sia impiegare un uomo e un badile. Un uomo in più senza un badile non scaverebbe nessuna buca, e neppure un badile senza uomo. Il numero totale di buche che possono essere prodotte corrisponderà pertanto al minimo tra il numero degli uomini e quello dei badili a disposizione. La funzione di produzione sarà:
q = (x1, x2) = min
Gli isoquanti vengono rappresentati in questo modo:
![]()
![]()
![]()
![]() x1
x1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x2
x2
e corrispondono esattamente al caso dei perfetti complementi nella teoria del consumatore.
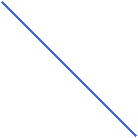
Supponiamo, ora, di produrre torte e che gli input siano teglie rotonde e teglie quadrate. La quantità di torte prodotte dipende unicamente dal numero totale delle teglie, e quindi la funzione di produzione sarà:
q = (x1, x2) = x1 + x2.
Gli isoquanti vengono rappresentati in questo modo:
![]()
 x1
x1

![]()
![]() x2
x2
e corrispondono esattamente al caso dei perfetti sostituti nella teoria del consumatore.
Se la funzione di produzione ha la forma:
q = (x1, x2) = A * x1a * x2b,
diremo che è una funzione di produzione Cobb-Douglas.
In questo caso, il parametro A misura la scala di produzione, cioè la quantità di output che può essere prodotta impiegando una unità di ciascun input.
I parametri a e b rappresentano la variazione del livello dell'output al variare delle quantità di input impiegate. Generalmente, poniamo: a + b = 1.
proprietà della tecnologia
1) Impossibilità di produrre senza l'impiego di fattori-
2) Irreversibilità: il processo produttivo non può essere invertito: se un dato ammontare di fattori da luogo ad un certo output, non è poi possibile trasformare nuovamente l'output negli input impiegati.
3). Le tecnologie sono monotone: aumentando la quantità impiegata di almeno uno degli input, dovrebbe essere possibile produrre una quantità di output almeno uguale a quella prodotta inizialmente. Si definisce, talvolta, questa proprietà come possibilità di eliminazione senza costo (free disposal)[1].
4) Additività: se esistono due attività di produzione ammissibili: y 1 e y 2 è possibile anche una attività y 3 che sia la somma delle due attività y 3 = y 1 + y 2
5) Divisibilità : data una attività y 1 ammissibile lo è anche una attività che appartiene allo stesso processo che sia una frazione di y 1 ad esempio ½ y 1
6) Convessità : ciò significa che se esistono due modi per produrre q unità di output, y 1 e y 2, allora la loro media ponderata produrrà almeno q unità di output.
Per illustrare questa ipotesi, supponiamo di produrre 1 unità di output impiegando a1 unità del fattore 1 e a2 unità del fattore 2, e di disporre di un altro modo per produrre 1 unità di output impiegando b1 unità del fattore 1 e b2 unità del fattore 2. Chiamiamo questi due modi di produrre tecniche di produzione.
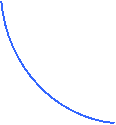
Supponiamo, inoltre, di poter aumentare arbitrariamente il livello dell'output, così che (100a1, 100a2) e (100b1, 100b2) unità di input produrranno 100 unità di output. Ma si noti ora che impiegando 25a1 + 75b1 unità del fattore 1 e 25a2 + 75b2 unità del fattore 2 è ancora possibile produrre 100 unità di output: 25 unità saranno prodotte impiegando la tecnica «a» e 75 impiegando la tecnica «b». Rappresentiamo il tutto graficamente:
![]()
x1
![]() a2
a2![]()

![]()
![]()
![]() (½a1 + ½b1, ½a2 + ½b2)
(½a1 + ½b1, ½a2 + ½b2)
![]() b2
b2
![]()
![]() a1 b1 x2
a1 b1 x2
Scegliendo il livello operativo di ciascuna delle due attività produttive sarà possibile produrre una data quantità di output in molti modi.
In particolare, ogni combinazione di input che si trovi sulla retta che unisce (a1, a2) e (b1, b2) rappresenta un modo realizzabile di produrre q unità di output. In questo tipo di tecnologia, dove è possibile aumentare o diminuire facilmente la produzione, ed i processi produttivi separati non interferiscono l'uno con l'altro, l'ipotesi di convessità risulta ragionevole.
IL SAGGIO MARGINALE DI SOSTITUZIONE TECNICA
il saggio marginale di sostituzione tecnica Supponiamo di impiegare la quantità (x1; x2) di input per produrre una data quantità di output. Supponiamo di voler ridurre di poco la quantità impiegata del fattore 1, usando al suo posto la quantità addizionale del fattore 2 esattamente necessaria per produrre la medesima quantità di output y.
Vogliamo, ora, vedere qual è la quantità addizionale del fattore 2, Dx2, che si deve impiegare se si vuole ridurre di Dx1 la quantità impiegata del fattore 1.
Il saggio al quale l'impresa deve sostituire un input con un altro per mantenere costante il livello dell'output viene definito come il saggio marginale di sostituzione tecnica. Esso è dato dal rapporto tra la diminuzione della quantità impiegata di x1 e l'aumento di x2 necessario affinché il livello di output del bene resti immutato, ossia:
SMST = Dx1/Dx2
.
Rappresentiamo, ora, su un piano cartesiano tutte le combinazioni dei fattori x1 e x2 che servono a produrre una stessa quantità di output, mediante lo strumento analitico dell'isoquanto:
![]()
 x1
x1
 A
A
![]()
![]()
![]()
![]()
Dx1
B

Dx2
![]() a
a
![]()
![]() x2
x2
In questo caso, il SMST misura l'inclinazione della corda che unisce i punti A e B, ovvero la tangente dell'angolo a che si forma quando la retta interseca l'asse delle ascisse.
Se prendiamo l'intervallo Dx2 sempre più piccolo, la retta r ruota intorno al punto A fino a diventare tangente alla curva proprio in quel punto per Dx2 infinitesimo, ovvero per Dx2
Quindi, per Dx2 il SMST rappresenta x1/ x2, cioè la derivata prima della funzione e graficamente la pendenza dell'isoquanto.
![]() x1
x1
A
![]()

B
![]()
![]()
![]() a b
a b
![]() x2
x2
rapporto tra il smst e pmg Sappiamo che lungo un isoquanto la variazione della produzione dev'essere sempre 0, quindi, abbiamo che:
Dy = Dy/Dx1 * Dx1 + Dy/Dx2 * Dx2 = 0
Infatti, se Dx1 è positiva, allora Dx2 è negativa e viceversa.
Dx1 * PMG x1 + Dx2 * PMG x2 = 0 = Dy
cioè:
![]()
.
Quindi il SMST tra due fattori produttivi è uguale al reciproco del rapporto tra le produttività marginali dei due fattori.
considerazioni sul smst Un'altra assunzione riguardante la tecnologia è quella del saggio marginale di sostituzione tecnica decrescente. Questa ipotesi afferma che, se si impiega una quantità minore del fattore 1, e si varia l'impiego del fattore 2, in modo da rimanere sullo stesso isoquanto, il SMST diminuisce.
In parole povere, l'ipotesi che il SMST sia decrescente significa che l'inclinazione dell'isoquanto deve aumentare in valore assoluto man mano che ci si sposta lungo l'isoquanto nella direzione che corrisponde all'aumento di x1 e diminuire in valore assoluto man mano che ci si sposta lungo l'isoquanto nella direzione che corrisponde all'aumento di x2. Questo equivale a dire che gli isoquanti hanno forma convessa. Graficamente, abbiamo:
![]() x1
x1

A
![]()

B
![]()
![]()
![]() a b
a b
![]() x2
x2
Vediamo, infatti, che, passando da A a B, cioè aumentando l'impiego del fattore 2, la pendenza dell'isoquanto, ovvero il SMST, diminuisce in valore assoluto.
Viceversa, passando da B a A, cioè aumentando l'impiego del fattore 1, la pendenza dell'isoquanto, ovvero il SMST, aumenta in valore assoluto.
rapporto fra il smst decrescente e il pmg decrescente Le ipotesi di SMST decrescente e PMG decrescente sono strettamente connesse, ma non coincidono esattamente.
L'ipotesi di PMG decrescente concerne la variazione del PMG che dipende dall'aumento della quantità impiegata di un fattore, se si mantiene l'altro a un livello prefissato.
L'ipotesi di SMST decrescente, invece, riguarda il modo in cui il rapporto dei prodotti marginali (l'inclinazione dell'isoquanto) varia, se si aumenta la quantità impiegata di un fattore e si fa variare la quantità impiegata dell'altro in modo da rimanere sullo stesso isoquanto.
GLI ISOCOSTI
Nell'acquisto dei fattori di produzione, l'impresa ha un vincolo, rappresentato dal fatto che essa ha una somma limitata da poter spendere nell'acquisto dei fattori stessi. Il vincolo, riferito a due fattori di produzione è:
C = w1x1 + w2x2
dove C rappresenta la spesa totale, ossia il costo totale sostenuto dall'impresa, x1 e x2 sono le quantità impiegate dei fattori produttivi, e w1 e w2 i rispettivi prezzi.
Con un semplice passaggio abbiamo:
w1x1 = C w2x2
da cui:
x1 = C/ w1 w2/w1 *
x2
.
Se rappresentiamo graficamente il vincolo, esso sarà una retta comunemente chiamata isocosto
![]()
x1
 C/w1
C/w1
![]() w2/w1
w2/w1
![]()
C/w2 x2
Se il produttore acquista 0 unità del fattore 2 e spende tutto il capitale C nel fattore 1, la quantità che acquisterà sarà C/w1. Il punto (0, C/w1) rappresenta l'intercetta dell'asse delle ordinate.
Se il produttore acquista 0 unità del fattore 1 e spende tutto il capitale C nel fattore 2, la quantità che acquisterà sarà C/w2. Il punto (C/w2, 0) rappresenta l'intercetta dell'asse delle ascisse.
w2/w1 è il coefficiente angolare dell'isocosto e rappresenta la quantità del fattore 1 a cui devo rinunciare per ottenere una unità aggiuntiva del fattore 2.
Riprendiamo il grafico precedente:
IMPOSSIBILI

![]()
![]() x1
x1
![]()
![]()
COMBINAZIONI POSSIBILI SPENDENDO PARTE DI C SOLO PER x1
![]()
 C/w1
C/w1
COMBINAZIONI POSSIBILI SPENDENDO TUTTO C
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 C/w2 x2
0 C/w2 x2
POSSIBILI
SPENDENDO
PARTE DI C
SOLO PER x2
|
COMBINAZIONI POSSIBILI SPENDENDO PARTE DI C |
In particolare:
i punti situati a destra dell'isocosto rappresentano combinazioni di fattori impossibili per il produttore, cioè tali da non poter essere acquistati dal produttore con il capitale di cui dispone;
i punti situati fra gli assi e l'isocosto rappresentano combinazioni di fattori possibili per il produttore, cioè tali da poter essere acquistati dal produttore spendendo parte del capitale di cui dispone;
i punti situati sull'isocosto rappresentano combinazioni di fattori possibili per il produttore, cioè tali da poter essere acquistati dal produttore spendendo tutto il capitale di cui dispone;
i punti situati sull'asse delle ascisse nell'intervallo aperto (0, C/w2) rappresentano combinazioni di fattori possibili per il produttore, cioè tali da poter essere acquistati dal produttore spendendo parte del capitale di cui dispone nell'acquisto del solo fattore 2;
i punti situati sull'asse delle ordinate nell'intervallo aperto (0, C/w1) rappresentano combinazioni di fattori possibili per il produttore, cioè tali da poter essere acquistati dal produttore spendendo parte del capitale di cui dispone nell'acquisto del solo fattore 1
esempio n°1 Supponiamo di variare il capitale del produttore C, da C a C', con C' > C, facendo rimanere invariati i prezzi.
Sia C = 120; C' = 200; w1 = w1' = 2; w2 = w2' = 4.
Avremo:
2x1 + 4x2 = 120, da cui:
x1 = 60 2x2 ( )
2x1 + 4x2 = 200, da cui:
x1 = 100 2x2 ( )
Graficamente:
![]() x1
x1
100


![]() -2 -2
-2 -2
30 50 x2
Quindi ogni volta che aumenta il capitale, restando invariati i prezzi, si ha una traslazione parallela (infatti, il coefficiente angolare rimane costante) dell'isocosto verso destra. In questo caso, aumenta il numero di combinazioni di fattori acquistabili dal produttore.
Analogamente, ogni volta che diminuisce il capitale, restando invariati i prezzi, si ha una traslazione parallela dell'isocosto verso sinistra. In quest'altro caso, diminuisce il numero di combinazioni di fattori acquistabili dal produttore.
esempio n°2 Supponiamo di far rimanere il capitale costante e di variare uno dei prezzi.
Sia C = C' = 100; w1 = w1' = 2; w2 = 4; w2' = 8.
Avremo:
2x1 + 4x2 = 100, da cui:
x1 = 50 2x2 ( )
2x1 + 8x2 = 100, da cui:
x1 = 50 4x2 ( )
Graficamente:
![]() x1
x1

 50
50
![]() -4 -2
-4 -2
12,5 25 x2
Quindi, a parità di capitale C, se aumenta il prezzo di uno dei due fattori, cambia l'inclinazione dell'isocosto e si riduce di consegunza il numero di combinazioni di fattori acquistabili dal produttore.
Analogamente, a parità di capitale C, se diminuisce il prezzo di uno dei due fattori, cambia l'inclinazione dell'isocosto ed aumenta di conseguenza il numero di combinazioni di fattori acquistabili dal produttore.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026